正确率60.0%在长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,直线$${{A}_{1}{C}}$$与平面$${{A}{{B}_{1}}{{D}_{1}}}$$的交点为$${{M}{,}{{A}_{1}}{{C}_{1}}}$$与$${{B}_{1}{{D}_{1}}}$$交于点$${{O}{,}}$$则下列结论正确的是()
B
A.$$A, ~ M, ~ O$$三点确定一个平面
B.$$A, ~ M, ~ O$$三点共线
C.$$D, ~ D_{1}, ~ O, ~ M$$四点共面
D.$$A, ~ B_{1}, ~ B, ~ M$$四点共面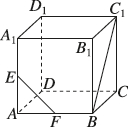
正确率60.0%空间中可以确定一个平面的条件是()
D
A.两两相交的三条直线
B.三条直线,其中的一条与另外两条直线分别相交
C.三个点
D.三条直线,它们两两相交,但不交于同一点
3、['空间四边形', '基本事实3', '基本事实1', '基本事实的推论']正确率80.0%下列说法中正确的是()
B
A.空间三点可以确定一个平面
B.梯形一定是平面图形
C.若$${{A}}$$,$${{B}}$$,$${{C}}$$,$${{D}}$$既在平面$${{α}}$$内,又在平面$${{β}}$$内,则平面$${{α}}$$和平面$${{β}}$$重合
D.两组对边都相等的四边形是平面图形
4、['立体几何中的四点共面、三点共线', '基本事实1', '基本事实的推论']正确率60.0%在如图所示的正方体和三棱锥中,$$P, Q, R, S$$分别是所在棱的中点,则这四个点不共面的是()
D
A.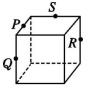
B.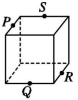
C.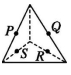
D.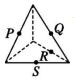
正确率60.0%如图所示$$, P, ~ Q, ~ R, ~ S$$分别是所在棱的中点,则这四个点不共面的是()
D
A.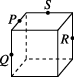
B.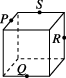
C.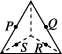
D.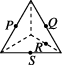
正确率60.0%在空间内,不一定能确定一个平面的是$${{(}{)}}$$
B
A.两条相交直线
B.不共线的四点
C.两条平行直线
D.直线和直线外一点
7、['空间两直线的共面、异面问题', '基本事实1', '基本事实的推论']正确率60.0%下列说法正确的是()
C
A.过一点和一条直线有且只有一个平面
B.过空间三点有且只有一个平面
C.不共面的四点中,任何三点不共线
D.两两相交的三条直线必共面
8、['平面的相关概念及表示', '基本事实2', '基本事实的推论']正确率60.0%下列图形不一定是平面图形的是()
C
A.三角形
B.圆
C.四边形
D.梯形
9、['平面的相关概念及表示', '基本事实3', '基本事实2', '基本事实1', '命题的真假性判断', '基本事实的推论']正确率60.0%下列说法中正确的个数为()
$${①}$$三角形一定是平面图形
$${②}$$若四边形的两对角线相交于一点,则该四边形是平面图形
$${③}$$圆心和圆上两点可确定一个平面
$${④}$$三条平行线最多可确定三个平面.
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
10、['棱柱的结构特征及其性质', '数学探究活动(一):正方体截面探究', '基本事实的推论']正确率60.0%在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$$P, \, \, Q, \, \, R$$分别是边$$A B, ~ A D, ~ B_{1} D_{1}$$的中点,那么过点$$P, \, \, Q, \, \, R$$的截面与正方体相交所成的图形是()
B
A.三角形
B.四边形
C.五边形
D.六边形
1. 解析:
在长方体 $$ABCD-A_1B_1C_1D_1$$ 中:
1. 点 $$O$$ 是 $$A_1C_1$$ 与 $$B_1D_1$$ 的交点,即 $$A_1B_1C_1D_1$$ 的中心。
2. 直线 $$A_1C$$ 与平面 $$AB_1D_1$$ 的交点为 $$M$$。
3. 由于 $$A_1C$$ 是空间对角线,$$M$$ 在 $$A_1C$$ 上,也在平面 $$AB_1D_1$$ 上。
4. 点 $$A$$、$$M$$、$$O$$ 都在平面 $$AA_1C_1C$$ 上,且 $$M$$ 在 $$A_1C$$ 上,$$O$$ 在 $$A_1C_1$$ 上,因此 $$A$$、$$M$$、$$O$$ 三点共线(选项 B 正确)。
5. 选项 A 虽然描述正确,但不如 B 直接。
6. 选项 C 中,$$D$$、$$D_1$$、$$O$$ 在底面上,但 $$M$$ 不在底面上,故不共面。
7. 选项 D 中,$$A$$、$$B_1$$、$$B$$ 在底面或侧面上,但 $$M$$ 不在这些平面上,故不共面。
答案:B
2. 解析:
确定平面的条件:
A. 两两相交的三条直线不一定共面(如三棱锥的三条侧棱)。
B. 一条直线与另外两条相交直线可以确定一个平面。
C. 三个点共线时不能确定唯一平面。
D. 三条直线两两相交且不共点时确定一个平面(如三角形的三边)。
答案:D
3. 解析:
A. 空间三点共线时不能确定唯一平面。
B. 梯形的两底边平行,一定是平面图形。
C. 若 $$A$$、$$B$$、$$C$$、$$D$$ 共线,则平面 $$α$$ 和 $$β$$ 不一定重合。
D. 两组对边相等的四边形可能是空间四边形(如菱形折叠后)。
答案:B
4. 解析:
通过几何分析:
A. 四点共面(均在正方体的对角面内)。
B. 四点不共面($$P$$、$$Q$$、$$R$$、$$S$$ 分布在不同平面上)。
C. 四点共面(均在棱锥的中截面内)。
D. 四点共面(均在棱锥的中截面内)。
答案:B
5. 解析:
与第 4 题相同,选项 B 的四点不共面。
答案:B
6. 解析:
A. 两条相交直线确定一个平面。
B. 不共线的四点可能不在同一平面上(如三棱锥的顶点)。
C. 两条平行直线确定一个平面。
D. 直线和直线外一点确定一个平面。
答案:B
7. 解析:
A. 若点在直线上,则有无数个平面。
B. 空间三点共线时不能确定唯一平面。
C. 不共面的四点中,任意三点不共线(否则四点共面)。
D. 两两相交的三条直线可能不共面(如三棱锥的三条侧棱)。
答案:C
8. 解析:
A. 三角形一定是平面图形。
B. 圆一定是平面图形。
C. 四边形可能是空间四边形。
D. 梯形一定是平面图形(两底边平行)。
答案:C
9. 解析:
① 三角形一定是平面图形(正确)。
② 四边形的两对角线相交则该四边形是平面图形(正确)。
③ 圆心和圆上两点若共线则不能确定唯一平面(错误)。
④ 三条平行线可确定一个或三个平面(正确)。
答案:C(①、②、④正确)
10. 解析:
在正方体中,连接 $$P$$、$$Q$$、$$R$$ 的截面会与正方体的多个面相交,形成五边形。
答案:C
.jpg)