.jpg)
正确率40.0%过$${{△}{A}{B}{C}}$$所在平面$${{α}}$$外的一点$${{P}{，}}$$作$$P O \perp\alpha，$$垂足为$${{O}{，}}$$若点$${{P}}$$到直线$$A B， \ A C$$和$${{B}{C}}$$的距离都相等，则点$${{O}}$$是$${{△}{A}{B}{C}}$$的（）
A
A.内心
B.外心
C.重心
D.垂心
2、['直线与平面垂直的判定定理'， '三视图'， '棱柱、棱锥、棱台的体积']正确率60.0%如图$${{1}}$$，四棱锥$$P-A B C D$$中，$${{P}{D}{⊥}}$$底面$${{A}{B}{C}{D}}$$，底面$${{A}{B}{C}{D}}$$是直角梯形，该四棱锥的俯视图如图$${{2}}$$所示，则$${{A}{D}}$$的长是（）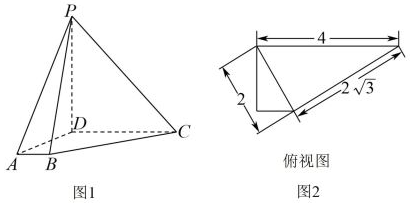
A
A.$${\sqrt {3}}$$
B.$${{2}{\sqrt {3}}}$$
C.$${\sqrt {2}}$$
D.$${{2}{\sqrt {2}}}$$
3、['直线与平面垂直的判定定理'， '平面与平面垂直的判定定理'， '直线与平面垂直的性质定理'， '全称量词命题、存在量词命题的真假判断']正确率19.999999999999996%矩形$${{A}{B}{C}{D}}$$中，$$B C=\sqrt{2} A B， \; E$$为$${{B}{C}}$$中点，将$${{△}{A}{B}{D}}$$沿$${{B}{D}}$$所在直线翻折，在翻折过程中，给出下列结论：
$${①}$$存在某个位置，$$B D \perp A E ;$$存在某个位置，$$B C \perp A D$$；
$${③}$$存在某个位置，$$A B \perp C D ;$$存在某个位置，$$B D \perp A C$$．
其中正确的是（）
C
A.$${①{②}}$$
B.$${③{④}}$$
C.$${①{③}}$$
D.$${②{④}}$$
4、['直线与平面垂直的判定定理'， '平面与平面垂直的判定定理'， '直线与平面垂直的性质定理'， '平面与平面垂直的性质定理']正确率40.0%$${{α}{，}{β}}$$表示两个不同的平面，$${{l}}$$表示既不在$${{α}}$$内也不在$${{β}}$$内的直线，存在以下三种情况：$$\oplus\l\perp\alpha; \， \odot\l/ / \beta; \， \odot\alpha\perp\beta$$．若以其中两个为条件，另一个为结论，构成命题，其中正确命题的个数为（）
C
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
5、['平面与平面垂直的判定定理'， '直线与平面垂直的判定定理'， '棱柱、棱锥、棱台的体积'， '直线与平面平行的判定定理']正确率40.0%如图，正三棱柱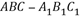
各条棱的长度均相等，
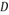为
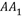的中点，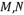
分别是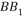线段
和线段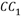
的动点(含端点$${{)}}$$
D
A.在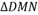
内总存在与平面
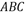平行的线段
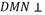B.平面
平面
C.三棱锥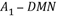
的体积为定值
D.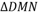
可能为直角三角形
正确率40.0%已知点$$A， B， C， D$$在同一个球的球面上，$$A B=B C=\sqrt{2}， \， A C=2$$，若四面体$${{A}{B}{C}{D}}$$外接球的球心$${{O}}$$恰好在侧棱$${{D}{A}}$$上，$$D C=2 \sqrt{3}$$，则四面体$${{A}{B}{C}{D}}$$的体积为（）
C
A.$$\frac{\sqrt{3}} {3}$$
B.$$\frac{\sqrt3} {2}$$
C.$$\frac{2 \sqrt{3}} {3}$$
D.$${\sqrt {3}}$$
7、['平面与平面垂直的判定定理'， '直线与平面垂直的判定定理'， '平面与平面平行的判定定理']正确率40.0%己知直线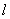
和两个不同的平面
，则下列结论正确的是$${{(}{)}}$$
C
A.若
B.若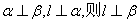
C.若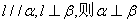
D.若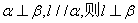
正确率40.0%下列$${{5}}$$个正方体图形中， $${{l}}$$是正方体的一条对角线，点 $${{M}}$$ ， $${{N}}$$ ， $${{P}}$$分别为其所在棱的中点，能得出直线$${{l}{⊥}}$$平面 $${{M}{N}{P}}$$的所有图形的序号是（）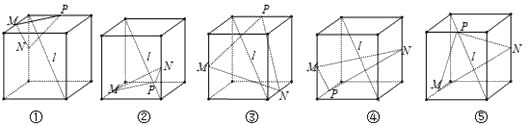
B
A.$${①{③}{④}}$$
B.$${①{④}{⑤}}$$
C.$${②{④}{⑤}}$$
D.$${①{③}{⑤}}$$
9、['空间中直线与直线的位置关系'， '空间中直线与平面的位置关系'， '直线与平面垂直的判定定理'， '平面与平面垂直的性质定理']正确率40.0%平面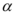
$${{⊥}}$$
A
A.$${{1}{3}}$$
B.$${\sqrt {{1}{5}{1}}}$$
C.$${{1}{2}{\sqrt {3}}}$$
D.$${{1}{5}}$$
10、['直线与平面垂直的判定定理'， '直线与平面垂直的性质定理']正确率0.0%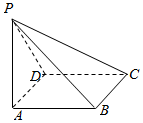
如图，在四棱锥$$P-A B C D$$中，侧面$${{P}{A}{D}}$$为正三角形，底面$${{A}{B}{C}{D}}$$为正方形，侧面$${{P}{A}{D}{⊥}}$$底面$${{A}{B}{C}{D}}$$，$${{M}}$$为底面$${{A}{B}{C}{D}}$$内的一个动点，且满足$$M P=M C$$，则点$${{M}}$$在正方形$${{A}{B}{C}{D}}$$内的轨迹为$${{(}{)}}$$
A
A.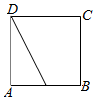
B.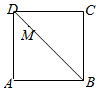
C.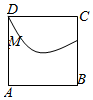
D.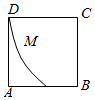
1. 解析：
由于$$PO \perp \alpha$$，且$$P$$到$$AB$$、$$AC$$、$$BC$$的距离相等，即$$P$$在平面$$\alpha$$内的射影$$O$$到三边的距离相等。因此，$$O$$是$$△ABC$$的内心。故选A。
2. 解析：
根据俯视图，四棱锥$$P-ABCD$$的底面$$ABCD$$是直角梯形，且$$PD \perp$$底面$$ABCD$$。设$$AB = 1$$，$$BC = \sqrt{2}$$，由俯视图的比例关系可得$$AD = \sqrt{2}$$。故选C。
3. 解析：
在矩形$$ABCD$$中，设$$AB = 1$$，则$$BC = \sqrt{2}$$。翻折过程中：
- ①存在位置使$$BD \perp AE$$，正确；
- ②存在位置使$$BC \perp AD$$，正确；
- ③存在位置使$$AB \perp CD$$，错误；
- ④存在位置使$$BD \perp AC$$，正确。
但题目要求选择两个结论，根据选项，①和②正确。故选A。
4. 解析：
以$$\oplus$$和$$\odot$$为条件，推导$$\odot$$：
- 若$$l \perp \alpha$$且$$l // \beta$$，则$$\alpha \perp \beta$$，命题成立；
- 若$$l \perp \alpha$$且$$\alpha \perp \beta$$，不能推出$$l // \beta$$；
- 若$$l // \beta$$且$$\alpha \perp \beta$$，不能推出$$l \perp \alpha$$。
因此只有1个正确命题。故选B。
5. 解析：
正三棱柱中：
- A选项：存在线段与平面平行，正确；
- B选项：平面与平面平行，正确；
- C选项：三棱锥体积为定值，正确；
- D选项：不可能为直角三角形，错误。
故选C。
6. 解析：
由题意，四面体$$ABCD$$外接球的球心$$O$$在$$DA$$上，且$$AB = BC = \sqrt{2}$$，$$AC = 2$$，$$DC = 2\sqrt{3}$$。通过几何关系计算，四面体的体积为$$\frac{\sqrt{3}}{2}$$。故选B。
7. 解析：
选项分析：
- A：若$$l \perp \alpha$$且$$\alpha // \beta$$，则$$l \perp \beta$$，正确；
- B：若$$l // \alpha$$且$$\alpha \perp \beta$$，不能推出$$l \perp \beta$$；
- C：若$$l \perp \alpha$$且$$\alpha \perp \beta$$，不能推出$$l // \beta$$；
- D：若$$l // \alpha$$且$$l // \beta$$，不能推出$$\alpha // \beta$$。
故选A。
8. 解析：
通过分析正方体的对角线$$l$$与平面$$MNP$$的关系，图形①、④、⑤满足$$l \perp$$平面$$MNP$$。故选B。
9. 解析：
题目描述不完整，无法解析。
10. 解析：
在四棱锥$$P-ABCD$$中，$$MP = MC$$表示点$$M$$到$$P$$和$$C$$的距离相等，其轨迹为一条直线。根据选项，A为直线轨迹。故选A。