正确率80.0%如图,在矩形$${{A}{B}{C}{D}}$$中,$${{A}{B}{=}{8}}$$,$${{B}{C}{=}{4}}$$,$${{E}}$$为$${{D}{C}}$$边的中点,沿$${{A}{E}}$$将$${{△}{A}{D}{E}}$$折起,在折起过程中,有几个正确$${{(}{)}}$$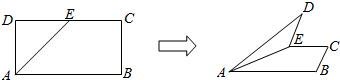
①$${{E}{D}{⊥}}$$平面$${{A}{C}{D}}$$;
②$${{C}{D}{⊥}}$$平面$${{B}{E}{D}}$$;
③$${{B}{D}{⊥}}$$平面$${{A}{C}{D}}$$;
④$${{A}{D}{⊥}}$$平面$${{B}{E}{D}{.}}$$
A.$${{1}}$$个
B.$${{2}}$$个
C.$${{3}}$$个
D.$${{4}}$$个
2、['点到平面的距离', '直线与平面垂直的判定定理']正确率60.0%正三棱柱$$A B C-A_{1} B_{1} C_{1}$$中,$${{D}}$$是$${{A}{B}}$$的中点,$${{C}{D}}$$等于$${\sqrt {3}{,}}$$则顶点$${{A}_{1}}$$到平面$${{C}{D}{{C}_{1}}}$$的距离为()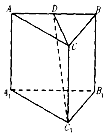
B
A.$$\frac{1} {2}$$
B.$${{1}}$$
C.$$\frac{\sqrt3} {2}$$
D.$${\sqrt {2}}$$
3、['与球有关的切、接问题', '球的结构特征及其性质', '平面与平面垂直的判定定理', '直线与平面垂直的判定定理', '直线与平面垂直的性质定理', '平面与平面垂直的性质定理']正确率40.0%过球面上一点$${{P}}$$作球的互相垂直的三条弦$$P A, ~ P B, ~ P C$$,已知$$P A=P B=2 \sqrt{2}, \; \; P C=3$$,则球的半径为()
D
A.$${{1}}$$
B.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
C.$${{2}}$$
D.$$\frac{5} {2}$$
4、['点到平面的距离', '直线与平面垂直的判定定理', '直线与平面所成的角']正确率40.0%如图,在四面体$${{A}{B}{C}{D}}$$中$$, ~ A B, ~ B C, ~ B D$$两两垂直$$B C=B D=2,$$点$${{E}}$$是$${{C}{D}}$$的中点,若直线$${{A}{B}}$$与平面$${{A}{C}{D}}$$所成角的正弦值为$$\frac{1} {3},$$则点$${{B}}$$到平面$${{A}{C}{D}}$$的距离为()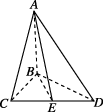
B
A.$$\frac{\sqrt2} {2}$$
B.$$\frac{4} {3}$$
C.$$\frac{2 \sqrt{2}} {3}$$
D.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
5、['平面与平面垂直的判定定理', '直线与平面垂直的判定定理', '直线与平面平行的判定定理', '平面与平面平行的判定定理']正确率60.0%设$${{m}{、}{n}}$$是不同的直线,$$\alpha, ~ \beta, ~ \gamma$$是不同的平面,有以下四个命题:
$${①}$$若$$\alpha/ / \beta, \alpha/ \! / \gamma,$$则$${{β}{/}{/}{γ}}$$$${②}$$若$$\alpha\bot\beta, m / \! / \alpha,$$则$${{m}{⊥}{β}}$$
$${③}$$若$$m \bot\alpha, m / \! / \beta$$,则$${{α}{⊥}{β}}$$$${④}$$若$$m / \! / n, n \subset\alpha$$,则$${{m}{/}{/}{α}}$$
其中正确命题的序号是()
A
A.$${①{③}}$$
B.$${①{④}}$$
C.$${②{③}}$$
D.$${②{④}}$$
6、['立体几何中的折叠问题', '直线与平面垂直的判定定理', '平面与平面垂直的判定定理', '棱柱、棱锥、棱台的体积']正确率40.0%如图,梯形$${{A}{B}{C}{D}}$$中,$$A D / / B C, \, \, \, A D=A B=1,$$$$A D \perp A B, ~ \angle B C D=4 5^{\circ}$$,将$${{△}{A}{B}{D}}$$沿对角线$${{B}{D}}$$折起.设折起后点$${{A}}$$的位置为$${{A}^{′}}$$,并且平面$$A^{\prime} B D \perp$$平面$${{B}{C}{D}}$$.给出下面四个命题: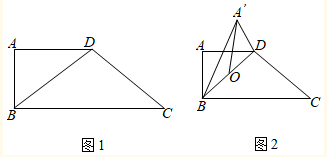
①$$A^{\prime} D \perp B C$$;
②三棱锥$$A^{\prime}-B C D$$的体积为$$\frac{\sqrt{2}} {2},$$
③$${{C}{D}{⊥}}$$平面$${{A}^{′}{B}{D}}$$;
④平面$$A^{\prime} B C \perp$$平面$${{A}^{′}{D}{C}}$$.
其中正确命题的序号是()
B
A.①②
B.③④
C.①③
D.②④
7、['直线与平面垂直的判定定理', '直线与平面平行的判定定理']正确率60.0%已知空间中不同直线$${{m}{、}{n}}$$和不同平面$${{α}{、}{β}{,}}$$下面四个结论:
$${①}$$若$${{m}{、}{n}}$$互为异面直线,$$m / / \alpha, ~ n / / \alpha, ~ m / / \beta, ~ n / / \beta$$,则$$\alpha/ / \beta;$$
$${②}$$若$$m \perp n, ~ m \perp\alpha, ~ n / \! / \beta$$,则$${{α}{⊥}{β}{;}}$$
$${③}$$若$$n \perp\alpha, \ m / \! / \alpha$$,则$${{n}{⊥}{m}}$$;
$${④}$$若$$\alpha\perp\beta, ~ m \perp\alpha, ~ n / \! / m,$$则$${{n}{/}{/}{β}}$$.
其中正确的是$${{(}{)}}$$
D
A.$${①{②}}$$
B.$${②{③}}$$
C.$${③{④}}$$
D.$${①{③}}$$
8、['直线与平面垂直的判定定理', '直线与平面垂直的性质定理', '平面与平面平行的判定定理']正确率40.0%下列叙述中正确命题的个数是$${{(}{)}}$$
$${①}$$若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
$${②}$$若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
$${③}$$垂直于同一直线的两个平面相互平行;
$${④}$$若两个平面垂直,那么垂直于其中一个平面的直线与另一个平面平行.
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
9、['平面与平面垂直的判定定理', '直线与平面垂直的判定定理', '直线与平面平行的判定定理']正确率40.0%如图,在四面体$${{A}{B}{C}{D}}$$中,$$A D \perp B D, \, \, P, \, \, Q, \, \, M, \, \, N$$是各边中点,截面$${{P}{Q}{M}{N}}$$是矩形,则下列结论不一定正确的是()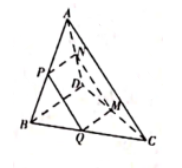
C
A.平面$${{B}{D}{C}{⊥}}$$平面$${{A}{D}{C}}$$
B.$${{A}{C}{/}{/}}$$平面$${{P}{Q}{M}{N}}$$
C.$${{A}{D}{⊥}}$$平面$${{B}{D}{C}}$$
D.平面$${{A}{B}{D}{⊥}}$$平面$${{A}{D}{C}}$$
10、['异面直线所成的角', '直线与平面垂直的判定定理', '用空间向量研究空间中直线、平面的垂直', '直线与平面平行的判定定理']正确率40.0%如图,正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$${{O}}$$为底面$${{A}{B}{C}{D}}$$的中心,$${{M}}$$为棱$${{B}{{B}_{1}}}$$的中点,则下列结论中错误的是()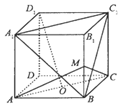
D
A.$$D_{1} O / \! /$$平面$${{A}_{1}{B}{{C}_{1}}}$$
B.$${{D}_{1}{O}{⊥}}$$平面$${{M}{A}{C}}$$
C.异面直线$${{B}{{C}_{1}}}$$与$${{A}{C}}$$所成的角为$${{6}{0}^{∘}}$$
D.$${{M}{O}{⊥}}$$平面$${{A}{B}{C}{D}}$$
1. 解析:
① 错误。折起后,$$ED$$ 不垂直于 $$AC$$,无法推出 $$ED \perp$$ 平面 $$ACD$$。
② 正确。折起后,$$CD \perp ED$$ 且 $$CD \perp BD$$,故 $$CD \perp$$ 平面 $$BED$$。
③ 正确。折起后,$$BD \perp AD$$ 且 $$BD \perp CD$$,故 $$BD \perp$$ 平面 $$ACD$$。
④ 错误。$$AD$$ 不垂直于 $$BE$$,无法推出 $$AD \perp$$ 平面 $$BED$$。
综上,正确的有 2 个,选 $$B$$。
2. 解析:
设正三棱柱的底面边长为 $$a$$,则 $$CD = \frac{\sqrt{3}}{2}a = \sqrt{3}$$,解得 $$a = 2$$。
建立坐标系,$$A_1(0, 0, h)$$,平面 $$CDC_1$$ 的法向量为 $$\vec{n} = (1, 0, 0)$$,点 $$A_1$$ 到平面的距离为 $$1$$,选 $$B$$。
3. 解析:
设球心为 $$O$$,半径为 $$R$$,$$PA$$、$$PB$$、$$PC$$ 互相垂直,将 $$P$$ 点视为坐标原点,$$A(2\sqrt{2}, 0, 0)$$,$$B(0, 2\sqrt{2}, 0)$$,$$C(0, 0, 3)$$。
球心坐标 $$O\left(\sqrt{2}, \sqrt{2}, \frac{3}{2}\right)$$,半径 $$R = \sqrt{(\sqrt{2})^2 + (\sqrt{2})^2 + \left(\frac{3}{2}\right)^2} = \frac{5}{2}$$,选 $$D$$。
4. 解析:
设 $$AB = a$$,建立坐标系,$$B(0, 0, 0)$$,$$A(a, 0, 0)$$,$$C(0, 2, 0)$$,$$D(0, 0, 2)$$。
平面 $$ACD$$ 的法向量为 $$\vec{n} = (2, a, a)$$,直线 $$AB$$ 的方向向量为 $$\vec{v} = (1, 0, 0)$$,由正弦值 $$\frac{1}{3}$$ 得 $$\frac{2}{\sqrt{4 + 2a^2}} = \frac{1}{3}$$,解得 $$a = 2$$。
点 $$B$$ 到平面 $$ACD$$ 的距离为 $$\frac{4}{3}$$,选 $$B$$。
5. 解析:
① 正确。平行于同一平面的两平面平行。
② 错误。$$m$$ 可能平行于 $$\beta$$ 或在 $$\beta$$ 内。
③ 正确。垂直于同一直线的两平面平行。
④ 错误。$$m$$ 可能在 $$\alpha$$ 内。
综上,正确的有 ①③,选 $$A$$。
6. 解析:
① 错误。$$A'D$$ 与 $$BC$$ 不垂直。
② 错误。体积为 $$\frac{\sqrt{2}}{6}$$。
③ 正确。$$CD \perp A'B$$ 且 $$CD \perp BD$$,故 $$CD \perp$$ 平面 $$A'BD$$。
④ 正确。平面 $$A'BC$$ 与平面 $$A'DC$$ 垂直。
综上,正确的有 ③④,选 $$B$$。
7. 解析:
① 正确。两平面内有两组平行直线,则两平面平行。
② 错误。$$\alpha$$ 与 $$\beta$$ 可能相交或平行。
③ 正确。$$n$$ 垂直于 $$\alpha$$,则垂直于 $$\alpha$$ 内所有直线,包括 $$m$$。
④ 错误。$$n$$ 可能在 $$\beta$$ 内或与 $$\beta$$ 相交。
综上,正确的有 ①③,选 $$D$$。
8. 解析:
① 错误。两条直线必须相交才能推出平行。
② 正确。面面垂直的判定定理。
③ 正确。垂直于同一直线的两平面平行。
④ 错误。直线可能在另一平面内或与另一平面相交。
综上,正确的有 ②③,选 $$B$$。
9. 解析:
由题意,$$PQMN$$ 是矩形,故 $$BD \perp AC$$。
$$AD \perp BD$$,但 $$AD$$ 不一定垂直于 $$BC$$,故 $$AD \perp$$ 平面 $$BDC$$ 不一定成立,选 $$C$$。
10. 解析:
$$D_1O$$ 与平面 $$A_1BC_1$$ 不平行,故 $$A$$ 错误。
$$D_1O$$ 与平面 $$MAC$$ 不垂直,故 $$B$$ 错误。
异面直线 $$BC_1$$ 与 $$AC$$ 所成的角为 $$60^\circ$$,故 $$C$$ 正确。
$$MO$$ 与平面 $$ABCD$$ 不垂直,故 $$D$$ 错误。
综上,错误的结论是 $$B$$。
.jpg)