正确率40.0%如图,在等腰直角$${{△}{A}{B}{O}}$$中,设$$\overrightarrow{O A}=\overrightarrow{a}, \, \, \, \overrightarrow{O B}=\overrightarrow{b}, \, \, \, | \overrightarrow{O A} |=| \overrightarrow{O B} |=1, \, \, \, C$$为$${{A}{B}}$$上靠近$${{A}}$$点的三等分点,过$${{C}}$$作$${{A}{B}}$$的垂线$${{l}}$$,设$${{P}}$$为垂线上任一点,$$\overrightarrow{O P}=\overrightarrow{p}$$,则$$\overrightarrow{p} \cdot\left( \overrightarrow{b}-\overrightarrow{a} \right)=$$()
B
A.$$\frac{1} {3}$$
B.$$- \frac{1} {3}$$
C.$$- \frac{3} {2}$$
D.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
2、['立体几何中的动态问题', '直线与平面垂直的定义', '直线与平面垂直的判定定理', '平面与平面平行的判定定理']正确率40.0%已知正四棱柱$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中$$\cdot\ \ A B=1, \ \ A A_{1}=2,$$点$${{P}{,}{Q}}$$分别是棱$$B B_{1}, ~ A B$$上的动点,则下列结论错误的是()
C
A.任意给定的点$${{P}{(}{P}}$$不在$${{B}}$$点),存在点$${{Q}{,}}$$使得$${{P}{Q}{/}{/}}$$平面$${{A}_{1}{{C}_{1}}{D}}$$
B.任意给定的点$${{Q}{(}{Q}}$$不在$${{B}}$$点),存在点$${{P}{,}}$$使得$${{P}{Q}{/}{/}}$$平面$${{A}_{1}{{C}_{1}}{D}}$$
C.任意给定的点$${{P}{,}}$$存在点$${{Q}{,}}$$使得$$C P \perp D_{1} Q$$
D.任意给定的点$${{Q}{,}}$$存在点$${{P}{,}}$$使得$$C P \perp D_{1} Q$$
3、['直线与平面垂直的定义', '直线与平面垂直的判定定理']正确率60.0%如图,如果$${{M}{C}}$$垂直于菱形$${{A}{B}{C}{D}}$$所在的平面,那么$${{M}{A}}$$与$${{B}{D}}$$()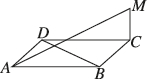
C
A.平行
B.垂直且相交
C.垂直且异面
D.相交但不垂直
4、['直线与平面垂直的定义', '直线与平面垂直的判定定理']正确率40.0%如图,在直三棱柱$$A B C-A_{1} B_{1} C_{1}$$中,侧棱长为$$2$$是$${{A}_{1}{{B}_{1}}}$$的中点$${,{F}}$$是$${{B}{{B}_{1}}}$$上的点$$, ~ A B_{1}, ~ D F$$交于点$${{E}{,}}$$若$${{A}{{B}_{1}}{⊥}}$$平面$$C_{1} D F,$$则线段$${{B}_{1}{F}}$$的长为()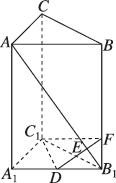
C
A.$$\frac{1} {3}$$
B.$$\frac{\sqrt3} {2}$$
C.$$\frac{1} {2}$$
D.$$\frac{\sqrt{3}} {3}$$
5、['立体几何位置关系的综合应用', '直线与平面垂直的定义']正确率80.0%直线$${{l}{⊥}}$$平面$${{α}{,}}$$直线$${{m}}$$$${{⊂}{a}{,}}$$则$${{l}}$$与$${{m}}$$不可能()
A
A.平行
B.相交
C.异面
D.垂直
6、['空间中直线与平面的位置关系', '直线与平面垂直的定义', '平面与平面垂直的判定定理']正确率40.0%已知$${{m}{,}{l}}$$是直线,$${{α}{,}{β}}$$是平面,给出下列命题:
$${①}$$若$${{l}}$$垂直于$${{α}{,}}$$则$${{l}}$$垂直于$${{α}}$$内的所有直线,
$${②}$$若$${{l}}$$平行于$${{α}{,}}$$则$${{l}}$$平行于$${{α}}$$内的所有直线
$${③}$$若$${{l}{⊂}{β}}$$,且$${{l}{⊥}{α}}$$,则$${{α}{⊥}{β}}$$
$${④}$$若$$m \subset\alpha, ~ l \subset\beta$$,且$$\alpha/ / \beta,$$则$${{m}{/}{/}{l}}$$
其中正确的命题的个数是()
C
A.$${{4}}$$
B.$${{3}}$$
C.$${{2}}$$
D.$${{1}}$$
7、['充分、必要条件的判定', '直线与平面垂直的定义']正确率40.0%$${{“}}$$直线$${{l}}$$与平面$${{α}}$$内无数条直线都垂直$${{”}}$$是$${{“}}$$直线$${{l}}$$与平面$${{α}}$$垂直$${{”}}$$的$${{(}{)}}$$条件
C
A.充要
B.充分非必要
C.必要非充分
D.既非充分又非必要
8、['棱锥的结构特征及其性质', '三垂线定理及其逆定理', '直线与平面垂直的定义', '直线与平面垂直的判定定理']正确率60.0%已知平面$${{A}{B}{C}}$$外一点$${{P}}$$,且$${{P}{H}{⊥}}$$平面$${{A}{B}{C}}$$于点$${{H}}$$.给出下列四个命题:$${①}$$若$$P A \perp B C, ~ P B \perp A C$$,则点$${{H}}$$是$${{△}{A}{B}{C}}$$的垂心;$${②}$$若$$P A. ~ P B. ~ P C$$两两互相垂直,则点$${{H}}$$是$${{△}{A}{B}{C}}$$的垂心;$${③}$$若$$\angle A B C=9 0^{\circ},$$点$${{H}}$$是$${{A}{C}}$$的中点,则$$P A=P B=P C, \, \, \oplus$$若$$P A=P B=P C$$,则点$${{H}}$$是$${{△}{A}{B}{C}}$$的外心.其中正确命题个数为$${{(}{)}}$$
D
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
9、['空间中直线与直线的位置关系', '充分、必要条件的判定', '直线与平面垂直的定义', '直线与平面垂直的判定定理', '直线与平面平行的性质定理']正确率60.0%已知平面$${{α}}$$,直线$$l, m, n$$,满足$$m / / \alpha, n / / \alpha$$,且$${{m}{,}{n}}$$互为异面直线,则$${{“}{l}{⊥}{m}}$$且$${{l}{⊥}{n}{”}}$$是$${{“}}$$$${{l}{⊥}{α}}$$$${{”}}$$的()
A
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.既不充分也不必要条件
10、['空间中直线与直线的位置关系', '空间中直线与平面的位置关系', '直线与平面垂直的定义']正确率40.0%已知$$\alpha, ~ \beta, ~ \gamma$$是三个不同的平面,命题“若$$\alpha/ / \beta,$$且$${{α}{⊥}{γ}{,}}$$则$${{β}{⊥}{γ}}$$”是真命题.若把$$\alpha, ~ \beta, ~ \gamma$$中的任意两个平面换成直线,另一个保持不变,则在所得到的所有新命题中,真命题的个数是()
C
A.$${{0}}$$个
B.$${{1}}$$个
C.$${{2}}$$个
D.$${{3}}$$个
1. 在等腰直角三角形 $$△ABO$$ 中,$$|\overrightarrow{OA}| = |\overrightarrow{OB}| = 1$$,且 $$\overrightarrow{OA} = \overrightarrow{a}$$,$$\overrightarrow{OB} = \overrightarrow{b}$$。由于是等腰直角三角形,$$\overrightarrow{a} \cdot \overrightarrow{b} = 0$$。
点 $$C$$ 是 $$AB$$ 上靠近 $$A$$ 的三等分点,因此 $$\overrightarrow{OC} = \overrightarrow{OA} + \frac{1}{3}(\overrightarrow{OB} - \overrightarrow{OA}) = \frac{2}{3}\overrightarrow{a} + \frac{1}{3}\overrightarrow{b}$$。
直线 $$l$$ 是 $$AB$$ 的垂线,因此方向向量为 $$\overrightarrow{b} - \overrightarrow{a}$$。设 $$P$$ 为 $$l$$ 上任一点,则 $$\overrightarrow{CP}$$ 与 $$\overrightarrow{b} - \overrightarrow{a}$$ 垂直,故 $$(\overrightarrow{p} - \overrightarrow{OC}) \cdot (\overrightarrow{b} - \overrightarrow{a}) = 0$$。
代入 $$\overrightarrow{OC}$$ 得 $$\overrightarrow{p} \cdot (\overrightarrow{b} - \overrightarrow{a}) = \overrightarrow{OC} \cdot (\overrightarrow{b} - \overrightarrow{a}) = \left(\frac{2}{3}\overrightarrow{a} + \frac{1}{3}\overrightarrow{b}\right) \cdot (\overrightarrow{b} - \overrightarrow{a}) = \frac{1}{3}|\overrightarrow{b}|^2 - \frac{2}{3}|\overrightarrow{a}|^2 = \frac{1}{3} - \frac{2}{3} = -\frac{1}{3}$$。
答案为 $$B$$。
2. 正四棱柱 $$ABCD-A_1B_1C_1D_1$$ 中,$$AB=1$$,$$AA_1=2$$。分析各选项:
A. 对于任意 $$P$$(不在 $$B$$ 点),存在 $$Q$$ 使得 $$PQ \parallel$$ 平面 $$A_1C_1D$$。因为平面 $$A_1C_1D$$ 的法向量可以通过向量 $$\overrightarrow{A_1D}$$ 和 $$\overrightarrow{A_1C_1}$$ 确定,只要 $$PQ$$ 与法向量垂直即可,故正确。
B. 对于任意 $$Q$$(不在 $$B$$ 点),存在 $$P$$ 使得 $$PQ \parallel$$ 平面 $$A_1C_1D$$。同理,可以通过调整 $$P$$ 的位置使 $$PQ$$ 与法向量垂直,故正确。
C. 对于任意 $$P$$,存在 $$Q$$ 使得 $$CP \perp D_1Q$$。设 $$P$$ 在 $$BB_1$$ 上,$$Q$$ 在 $$AB$$ 上,通过向量计算可以找到满足条件的 $$Q$$,故正确。
D. 对于任意 $$Q$$,存在 $$P$$ 使得 $$CP \perp D_1Q$$。当 $$Q$$ 接近 $$A$$ 时,$$D_1Q$$ 的方向可能无法与 $$CP$$ 垂直,故错误。
答案为 $$D$$。
3. 菱形 $$ABCD$$ 中,$$MC \perp$$ 平面 $$ABCD$$,因此 $$MC \perp BD$$。由于菱形的对角线 $$BD$$ 与 $$AC$$ 垂直,且 $$MA$$ 在平面 $$MAC$$ 内,$$BD$$ 与 $$MA$$ 不在同一平面内且方向垂直,故 $$MA$$ 与 $$BD$$ 垂直且异面。
答案为 $$C$$。
4. 直三棱柱 $$ABC-A_1B_1C_1$$ 中,$$AB_1 \perp$$ 平面 $$C_1DF$$,因此 $$AB_1 \perp DF$$。设 $$B_1F = x$$,通过坐标系法或向量法可以解得 $$x = \frac{1}{2}$$。
答案为 $$C$$。
5. 直线 $$l \perp$$ 平面 $$\alpha$$,直线 $$m \subset \alpha$$,则 $$l$$ 与 $$m$$ 必定垂直,不可能平行。
答案为 $$A$$。
6. 分析各命题:
① 若 $$l \perp \alpha$$,则 $$l$$ 垂直于 $$\alpha$$ 内所有直线,正确。
② 若 $$l \parallel \alpha$$,$$l$$ 不一定平行于 $$\alpha$$ 内所有直线,错误。
③ 若 $$l \subset \beta$$ 且 $$l \perp \alpha$$,则 $$\alpha \perp \beta$$,正确。
④ 若 $$m \subset \alpha$$,$$l \subset \beta$$,且 $$\alpha \parallel \beta$$,则 $$m \parallel l$$ 或异面,错误。
正确的命题有 2 个。
答案为 $$C$$。
7. 直线 $$l$$ 与平面 $$\alpha$$ 内无数条直线垂直,不一定与 $$\alpha$$ 垂直(可能斜交);但若 $$l \perp \alpha$$,则与 $$\alpha$$ 内所有直线垂直。因此是必要非充分条件。
答案为 $$C$$。
8. 分析各命题:
① 若 $$PA \perp BC$$,$$PB \perp AC$$,则 $$H$$ 是垂心,正确。
② 若 $$PA$$、$$PB$$、$$PC$$ 两两垂直,$$H$$ 不一定是垂心,错误。
③ 若 $$\angle ABC = 90^\circ$$ 且 $$H$$ 是 $$AC$$ 中点,则 $$PA = PB = PC$$,正确。
④ 若 $$PA = PB = PC$$,则 $$H$$ 是外心,正确。
正确的命题有 3 个。
答案为 $$C$$。
9. 若 $$l \perp m$$ 且 $$l \perp n$$,由于 $$m$$ 和 $$n$$ 是异面直线,可以推出 $$l \perp \alpha$$(充要条件)。
答案为 $$A$$。
10. 原命题为真。将 $$\alpha$$、$$\beta$$、$$\gamma$$ 中的任意两个换成直线:
1. 若 $$\alpha$$ 和 $$\beta$$ 为直线,$$\gamma$$ 为平面,命题不成立。
2. 若 $$\alpha$$ 和 $$\gamma$$ 为直线,$$\beta$$ 为平面,命题成立。
3. 若 $$\beta$$ 和 $$\gamma$$ 为直线,$$\alpha$$ 为平面,命题不成立。
因此有 1 个真命题。
答案为 $$B$$。
.jpg)