正确率40.0%已知直线$${{l}}$$,平面$${{α}{.}}$$则$$\omega l \perp\alpha"$$是$${{“}{∃}}$$直线$$m \subset\alpha, ~ l \perp m "$$的
A
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
正确率60.0%三棱锥$$P-A B C$$中,若$$P A=P B=P C$$,则$${{P}}$$在底面$${{A}{B}{C}}$$上的投影$${{O}}$$为$${{△}{A}{B}{C}}$$的()
B
A.垂心
B.外心
C.内心
D.重心
3、['直线与平面垂直的定义', '直线与平面垂直的判定定理']正确率40.0%过$${{△}{A}{B}{C}}$$所在平面$${{α}}$$外的一点$${{P}{,}}$$作$$P O \perp\alpha,$$垂足为$${{O}{,}}$$若点$${{P}}$$到直线$$A B, \ A C$$和$${{B}{C}}$$的距离都相等,则点$${{O}}$$是$${{△}{A}{B}{C}}$$的()
A
A.内心
B.外心
C.重心
D.垂心
4、['直线与平面垂直的定义', '直线与平面垂直的判定定理', '平面与平面平行的性质定理', '直线与平面平行的判定定理', '平面与平面平行的判定定理']正确率60.0%在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$${{A}{C}}$$与$${{B}{D}}$$的交点为$${{O}{,}}$$关于直线$${{A}_{1}{O}{,}}$$下列说法正确的是()
B
A.$$A_{1} O / / D_{1} C$$
B.$$A_{1} O / \! /$$平面$${{B}_{1}{C}{{D}_{1}}}$$
C.$$A_{1} O \perp B C$$
D.$${{A}_{1}{O}{⊥}}$$平面$${{A}{{B}_{1}}{{D}_{1}}}$$
5、['直线与平面垂直的定义', '直线与平面垂直的判定定理']正确率60.0%如图,如果$${{M}{C}}$$垂直于菱形$${{A}{B}{C}{D}}$$所在的平面,那么$${{M}{A}}$$与$${{B}{D}}$$()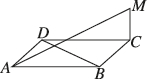
C
A.平行
B.垂直且相交
C.垂直且异面
D.相交但不垂直
6、['直线与平面垂直的定义']正确率60.0%若直线$${{a}}$$与平面$${{α}}$$不垂直,则平面$${{α}}$$内与直线$${{a}}$$垂直的直线有()
C
A.$${{0}}$$条
B.$${{1}}$$条
C.无数条
D.不确定
7、['与球有关的切、接问题', '直线与平面垂直的定义', '球的表面积']正确率40.0%在四面体$$S-A B C$$中,$${{S}{A}{⊥}}$$平面$${{A}{B}{C}}$$,$$\angle B A C=1 2 0^{\circ}$$,$${{A}{B}{=}{1}}$$,$${{A}{C}{=}{2}}$$,$${{S}{A}{=}{3}}$$,则该四面体外接球面积为()
B
A.$${\frac{5 0} {3}} \pi$$
B.$$\frac{5 5} {3} \pi$$
C.$$\frac{6 5} {3} \pi$$
D.$$\frac{7 0} {3} \pi$$
8、['充分、必要条件的判定', '直线与平面垂直的定义']正确率40.0%$${{“}}$$直线$${{l}}$$与平面$${{α}}$$内无数条直线都垂直$${{”}}$$是$${{“}}$$直线$${{l}}$$与平面$${{α}}$$垂直$${{”}}$$的$${{(}{)}}$$条件
C
A.充要
B.充分非必要
C.必要非充分
D.既非充分又非必要
9、['基本事实4', '异面直线垂直', '直线与平面垂直的定义', '直线与平面垂直的判定定理', '直线与平面平行的判定定理']正确率40.0%如图,在长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$$A A_{1}=2 A B, \, \, \, A B=B C$$,则下列结论中正确的是()
C
A.$$B D_{1} / / B_{1} C$$
B.$$A_{1} D_{1} / /$$平面$${{A}{{B}_{1}}{C}}$$
C.$$B D_{1} \perp A C$$
D.$${{B}{{D}_{1}}{⊥}}$$平面$${{A}{{B}_{1}}{C}}$$
10、['直线与平面垂直的定义', '直线与平面所成的角']正确率60.0%若斜线段$${{A}{B}}$$是它在平面$${{α}}$$上的射影长的$${{2}}$$倍,则$${{A}{B}}$$与平面$${{α}}$$所成的角是()
A
A.$${{6}{0}^{∘}}$$
B.$${{4}{5}^{∘}}$$
C.$${{3}{0}^{∘}}$$
D.$${{1}{2}{0}^{∘}}$$
1. 解析:
题目中“$$l \perp \alpha$$”表示直线 $$l$$ 垂直于平面 $$\alpha$$,这意味着 $$l$$ 垂直于 $$\alpha$$ 内的所有直线。而“存在直线 $$m \subset \alpha$$ 使得 $$l \perp m$$”仅要求 $$l$$ 垂直于 $$\alpha$$ 内的某一条直线,显然前者是后者的充分条件,但后者不能推出前者(因为 $$l$$ 可能仅与 $$\alpha$$ 内的一条直线垂直而不与整个平面垂直)。因此,正确答案是 A。
2. 解析:
若 $$PA = PB = PC$$,则点 $$P$$ 在底面的投影 $$O$$ 到 $$A$$、$$B$$、$$C$$ 的距离相等(因为 $$OA$$、$$OB$$、$$OC$$ 是斜边相等的直角三角形的直角边)。因此,$$O$$ 是 $$\triangle ABC$$ 的外心。正确答案是 B。
3. 解析:
$$PO \perp \alpha$$,且 $$P$$ 到 $$AB$$、$$AC$$、$$BC$$ 的距离相等,意味着 $$O$$ 到这三条边的距离相等(因为距离是通过垂线段定义的)。因此,$$O$$ 是 $$\triangle ABC$$ 的内心(到三边距离相等的点)。正确答案是 A。
4. 解析:
在正方体中,$$A_1O$$ 是体对角线的一部分。通过几何关系可以证明:
- $$A_1O$$ 与 $$D_1C$$ 不平行(排除 A);
- $$A_1O$$ 与平面 $$B_1CD_1$$ 相交(排除 B);
- $$A_1O$$ 与 $$BC$$ 不垂直(排除 C);
- $$A_1O$$ 垂直于平面 $$AB_1D_1$$(因为 $$A_1O$$ 是 $$AB_1D_1$$ 的法向量)。
正确答案是 D。
5. 解析:
在菱形 $$ABCD$$ 中,对角线 $$BD$$ 与 $$AC$$ 垂直。由于 $$MC$$ 垂直于平面 $$ABCD$$,$$MC$$ 与 $$BD$$ 垂直。因此,$$BD$$ 垂直于平面 $$MAC$$,从而 $$BD$$ 与 $$MA$$ 垂直。由于 $$MA$$ 和 $$BD$$ 不在同一平面内且不相交,它们是异面直线。正确答案是 C。
6. 解析:
若直线 $$a$$ 与平面 $$\alpha$$ 不垂直,则 $$a$$ 在 $$\alpha$$ 内存在无数条与之垂直的直线(只需在 $$\alpha$$ 内取与 $$a$$ 的法向量垂直的方向即可)。正确答案是 C。
7. 解析:
首先计算 $$\triangle ABC$$ 的外接圆半径:
由余弦定理,$$BC = \sqrt{AB^2 + AC^2 - 2 \cdot AB \cdot AC \cdot \cos 120^\circ} = \sqrt{1 + 4 + 2} = \sqrt{7}$$。
外接圆半径 $$R = \frac{BC}{2 \sin A} = \frac{\sqrt{7}}{2 \cdot \frac{\sqrt{3}}{2}} = \frac{\sqrt{21}}{3}$$。
由于 $$SA$$ 垂直于平面 $$ABC$$,外接球半径 $$R_{\text{球}} = \sqrt{R^2 + \left(\frac{SA}{2}\right)^2} = \sqrt{\frac{7}{3} + \frac{9}{4}} = \sqrt{\frac{55}{12}}$$。
外接球面积 $$S = 4\pi R_{\text{球}}^2 = \frac{55}{3}\pi$$。正确答案是 B。
8. 解析:
“直线 $$l$$ 与平面 $$\alpha$$ 内无数条直线垂直”不能推出“$$l$$ 与 $$\alpha$$ 垂直”(因为可能只是与一个平面内的一个方向族垂直),但“$$l$$ 与 $$\alpha$$ 垂直”可以推出“$$l$$ 与 $$\alpha$$ 内无数条直线垂直”。因此是必要非充分条件。正确答案是 C。
9. 解析:
在长方体中:
- $$BD_1$$ 与 $$B_1C$$ 不平行(排除 A);
- $$A_1D_1$$ 平行于平面 $$AB_1C$$(因为 $$A_1D_1 \parallel AD$$ 且 $$AD$$ 与平面 $$AB_1C$$ 平行);
- $$BD_1$$ 与 $$AC$$ 不垂直(排除 C);
- $$BD_1$$ 不垂直于平面 $$AB_1C$$(排除 D)。
正确答案是 B。
10. 解析:
设斜线段 $$AB$$ 与平面 $$\alpha$$ 的夹角为 $$\theta$$,射影长为 $$x$$,则 $$AB = 2x$$。由几何关系,$$\cos \theta = \frac{x}{2x} = \frac{1}{2}$$,因此 $$\theta = 60^\circ$$。正确答案是 A。
.jpg)