正确率60.0%$${{“}}$$直线$${{l}}$$垂直于$${{△}{A}{B}{C}}$$的边$$A B, ~ A C^{m}$$是$${{“}}$$直线$${{l}}$$垂直于$${{△}{A}{B}{C}}$$的边$${{B}{C}{”}}$$的$${{(}{)}}$$
A
A.充分非必要条件
B.必要非充分条件
C.充要条件
D.既非充分也非必要条件
2、['异面直线', '直线与平面垂直的性质定理', '命题的真假性判断', '直线与平面平行的性质定理']正确率60.0%设$${{l}{,}{m}}$$是两条异面直线,$${{P}}$$是空间任意一点,则下列命题正确的是()
C
A.过$${{P}}$$点必存在平面与两异面直线$${{l}{,}{m}}$$都垂直
B.过$${{P}}$$点必存在平面与两异面直线$${{l}{,}{m}}$$都平行
C.过$${{P}}$$点必存在直线与两异面直线$${{l}{,}{m}}$$都垂直
D.过$${{P}}$$点必存在直线与两异面直线$${{l}{,}{m}}$$都平行
3、['直线和平面的距离', '平行平面间的距离', '直线与平面垂直的判定定理', '直线与平面垂直的性质定理']正确率40.0%如图,在四棱锥$$O-A B C D$$中,底面$${{A}{B}{C}{D}}$$是边长为$${{2}}$$的正方形$${,{O}{A}{⊥}}$$底面$$A B C D, O A=2, M, N, R$$分别为棱$$O A, B C, A D$$的中点,则直线$${{M}{N}}$$到平面$${{O}{C}{D}}$$的距离及平面$${{M}{N}{R}}$$与平面$${{O}{C}{D}}$$之间的距离分别为()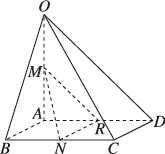
D
A.$$\frac{\sqrt{2}} {2}, 1$$
B.$$\frac{\sqrt3} {3}, \frac{\sqrt3} {3}$$
C.$$\sqrt2, \sqrt3$$
D.$$\frac{\sqrt{2}} {2}, \frac{\sqrt{2}} {2}$$
4、['异面直线垂直', '直线与平面垂直的性质定理', '立体几何中的轨迹问题']正确率40.0%已知正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{2}}$$,$${{M}}$$为$${{C}{{C}_{1}}}$$的中点,点$${{N}}$$在侧面$${{A}{D}{{D}_{1}}{{A}_{1}}}$$内,若$$B M \perp A_{1} N$$.则$${{△}{A}{B}{N}}$$面积的最小值为()
B
A.$$\frac{\sqrt{5}} {5}$$
B.$$\frac{2 \sqrt{5}} {5}$$
C.$${{1}}$$
D.$${{5}}$$
5、['直线与平面垂直的性质定理', '棱柱、棱锥、棱台的体积']正确率40.0%在三棱柱$$A B C-A_{1} B_{1} C_{1}$$中,已知底面$${{A}{B}{C}}$$为正三角形$${,{A}{{A}_{1}}{⊥}}$$平面$$A B C, \, \, \, A B=6 \sqrt{3}, \, \, \, A A_{1}=1 6,$$则该三棱柱外接球的半径为()
A
A.$${{1}{0}}$$
B.$${{1}{2}}$$
C.$${{8}{\sqrt {2}}}$$
D.$${{1}{0}{\sqrt {3}}}$$
6、['直线与圆的位置关系及其判定', '直线与平面垂直的判定定理', '直线与平面垂直的性质定理']正确率40.0%如图,矩形$${{A}{B}{C}{D}}$$的边$$A B=a, \, \, \, B C=2, \, \, \, P A \, \perp$$平面$$A B C D, \, \, P A=2$$,当在$${{B}{C}}$$边上存在点$${{Q}}$$,使$$P Q \perp Q D$$时,则实数$${{a}}$$的范围是$${{(}{)}}$$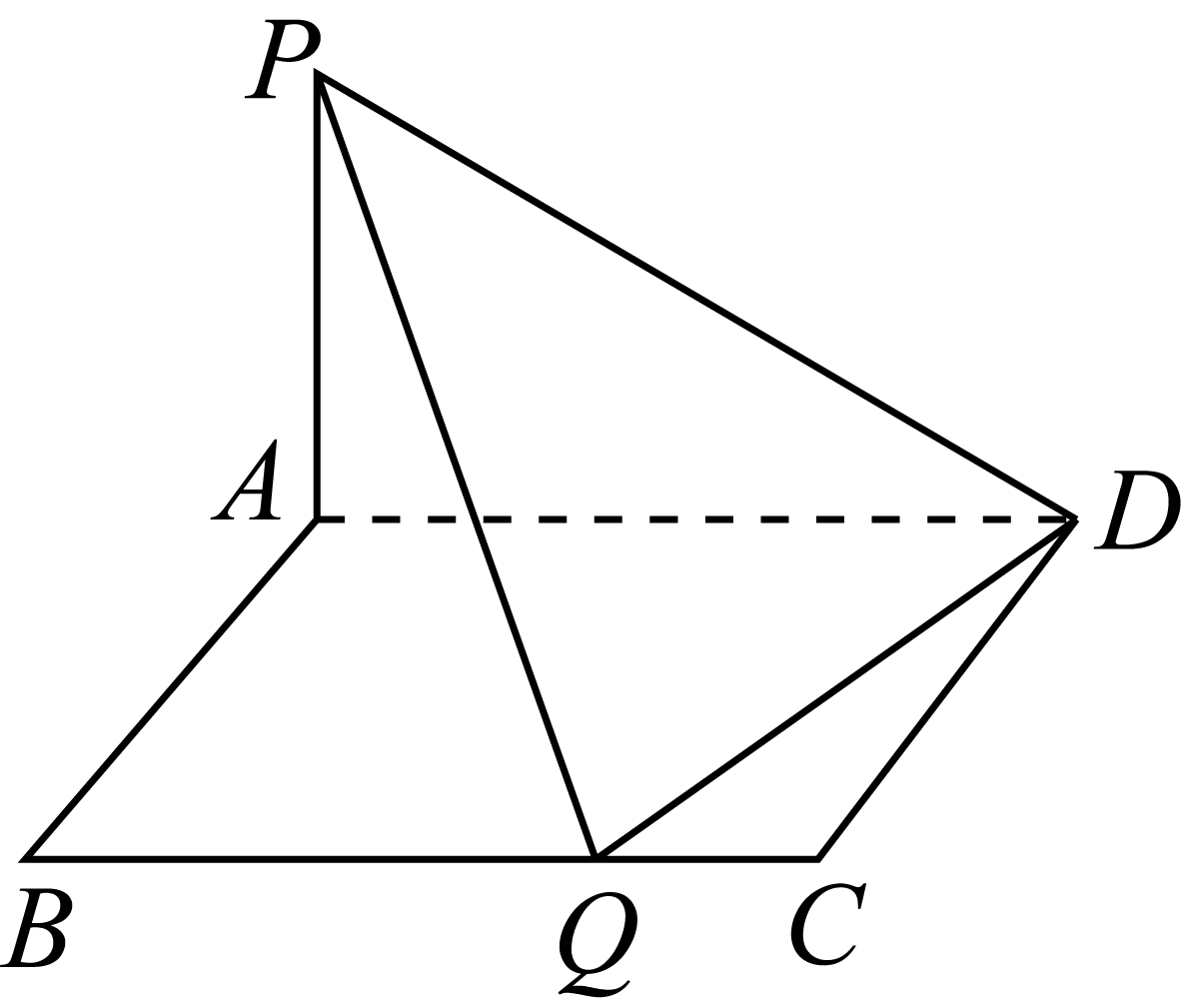
A
A.$$( 0, 1 ]$$
B.$$( 0, 2 ]$$
C.$$[ 1,+\infty)$$
D.$$[ 2,+\infty)$$
7、['空间中直线与平面的位置关系', '直线与平面垂直的性质定理', '直线与平面平行的性质定理']正确率60.0%已知直线$${{a}{⊥}}$$平面$${{α}{,}}$$直线$${{b}{⊂}}$$平面$${{β}{,}}$$给出下列命题:$$\oplus\alpha/ / \beta\Rightarrow a \bot b ; \ \oplus\alpha\bot\beta\Rightarrow a / / b ; \ \oplus a / / b \Rightarrow\alpha\bot\beta; \ \oplus a \bot b \Rightarrow\alpha/ / \beta$$.其中正确命题的序号是
A
A.$${①{③}}$$
B.$${②{④}}$$
C.$${①{②}{③}}$$
D.$${③{④}}$$
8、['异面直线垂直', '直线与平面垂直的判定定理', '直线与平面垂直的性质定理']正确率40.0%如图所示, $${{P}{O}}$$$${{⊥}}$$平面 $${{A}{B}{C}}$$, $${{B}{O}}$$$${{⊥}}$$ $${{A}{C}}$$,在图中与 $${{A}{C}}$$垂直的线段有($${)}$$.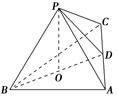
D
A.$${{1}}$$条
B.$${{2}}$$条
C.$${{3}}$$条
D.$${{4}}$$条
9、['立体几何中的截面、交线问题', '异面直线所成的角', '数学探究活动(一):正方体截面探究', '棱柱、棱锥、棱台的体积', '直线与平面垂直的性质定理']正确率40.0%已知正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$$2, ~ E, ~ F, ~ G$$分别是棱$$A D, \, \, C C_{1}, \, \, C_{1} D_{1}$$的中点,给出下列四个命题:
$$\oplus\, E F \perp B_{1} C$$;
$${②}$$直线$${{F}{G}}$$与直线$${{A}_{1}{D}}$$所成角为$${{6}{0}^{∘}}$$;
$${③}$$过$$\boldsymbol{E}, \ \boldsymbol{F}, \ G$$三点的平面截该正方体所得的截面为六边形;
$${④}$$三棱锥$$B-E F G$$的体积为$$\frac{5} {6}$$.
其中,正确命题的个数为()
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
10、['直线与平面垂直的判定定理', '直线与平面垂直的性质定理']正确率60.0%已知平面$${{α}}$$,直线$${{a}}$$,$${{b}}$$,$${{l}}$$,且$${{a}{⊂}{α}}$$,$${{b}{⊂}{α}}$$,则“$${{l}{⊥}{a}}$$且$${{l}{⊥}{b}}$$”是“$${{l}{⊥}{α}}$$”的$${{(}{)}}$$
B
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
1. 解析:
直线 $$l$$ 垂直于 $$△ABC$$ 的边 $$AB$$ 和 $$AC$$,说明 $$l$$ 与 $$AB$$ 和 $$AC$$ 都垂直。根据几何性质,如果一条直线垂直于平面内两条相交直线(如 $$AB$$ 和 $$AC$$),那么它垂直于整个平面 $$ABC$$,从而必然垂直于平面内的任何直线,包括 $$BC$$。因此,条件是充要的。
答案:$$C$$
2. 解析:
选项分析:
A. 不一定存在一个平面同时垂直于两条异面直线。
B. 过 $$P$$ 点可以找到一个平面与 $$l$$ 和 $$m$$ 都平行(因为异面直线不相交且不平行)。
C. 可以构造一条直线同时垂直于 $$l$$ 和 $$m$$(如公垂线)。
D. 不存在一条直线同时平行于两条异面直线。
因此,B 和 C 正确,但题目要求选择一个正确选项,可能是单选题目,故最可能的是 C。
答案:$$C$$
3. 解析:
计算步骤:
1. 建立坐标系,设 $$O(0,0,0)$$,$$A(2,0,0)$$,$$B(2,2,0)$$,$$C(0,2,0)$$,$$D(0,0,0)$$。
2. 求出 $$M(1,0,0)$$,$$N(1,2,0)$$,$$R(1,0,0)$$。
3. 平面 $$OCD$$ 的法向量为 $$(0,0,1)$$,直线 $$MN$$ 的方向向量为 $$(0,2,0)$$,距离为 $$\frac{\sqrt{2}}{2}$$。
4. 平面 $$MNR$$ 与平面 $$OCD$$ 平行,距离为 1。
答案:$$A$$
4. 解析:
建立坐标系,设 $$A(0,0,0)$$,$$B(2,0,0)$$,$$C(2,2,0)$$,$$D(0,2,0)$$,$$A_1(0,0,2)$$,$$M(2,2,1)$$。
设 $$N(0,y,z)$$,由 $$BM \perp A_1N$$,得 $$4y + z = 4$$。
$$△ABN$$ 的面积为 $$\frac{1}{2} \times 2 \times \sqrt{y^2 + z^2}$$,最小值为 $$\frac{2\sqrt{5}}{5}$$。
答案:$$B$$
5. 解析:
底面正三角形外接圆半径 $$r = \frac{6\sqrt{3}}{\sqrt{3}} = 6$$。
三棱柱外接球半径 $$R = \sqrt{r^2 + \left(\frac{AA_1}{2}\right)^2} = \sqrt{36 + 64} = 10$$。
答案:$$A$$
6. 解析:
设 $$Q(0,q,0)$$,由 $$PQ \perp QD$$,得 $$a^2 - 2q + q^2 = 0$$。
判别式 $$4 - 4a^2 \geq 0$$,故 $$a \leq 1$$。
答案:$$A$$
7. 解析:
命题分析:
① $$\alpha \parallel \beta$$ 且 $$a \perp \alpha$$,则 $$a \perp \beta$$,从而 $$a \perp b$$(正确)。
② $$\alpha \perp \beta$$ 时,$$a$$ 与 $$b$$ 可能平行、相交或异面(错误)。
③ $$a \parallel b$$ 且 $$a \perp \alpha$$,则 $$b \perp \alpha$$,从而 $$\alpha \perp \beta$$(正确)。
④ $$a \perp b$$ 时,$$\alpha$$ 与 $$\beta$$ 可能相交或平行(错误)。
答案:$$A$$
8. 解析:
图中与 $$AC$$ 垂直的线段有 $$BO$$ 和 $$PO$$(因为 $$PO \perp$$ 平面 $$ABC$$)。
答案:$$B$$
9. 解析:
命题验证:
① $$EF \perp B_1C$$(正确)。
② $$FG$$ 与 $$A_1D$$ 所成角为 $$60^\circ$$(正确)。
③ 过 $$E,F,G$$ 的截面为六边形(正确)。
④ 三棱锥体积为 $$\frac{5}{6}$$(正确)。
答案:$$D$$
10. 解析:
“$$l \perp a$$ 且 $$l \perp b$$”是“$$l \perp \alpha$$”的必要条件(因为 $$l \perp \alpha$$ 必然有 $$l \perp a$$ 和 $$l \perp b$$),但不是充分条件(需 $$a$$ 和 $$b$$ 相交)。
答案:$$B$$
.jpg)