正确率40.0%在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,下列结论错误的是()
C
A.$$A_{1} C_{1} / /$$平面$${{A}{B}{C}{D}}$$
B.$$A C_{1} \perp B D$$
C.$${{A}{{C}_{1}}}$$与$${{C}{D}}$$成45°角
D.$${{A}_{1}{{C}_{1}}}$$与$${{B}_{1}{C}}$$成60°角
2、['异面直线垂直']正确率19.999999999999996%在矩形$${{A}{B}{C}{D}}$$中$$, \, \, A B=2, \, \, \, B C=2 \sqrt{2},$$将$${{△}{A}{B}{D}}$$沿矩形的对角线$${{B}{D}}$$所在的直线进行翻折,在翻折过程中,下列说法正确的是()
B
A.存在某个位置,使得直线$${{B}{D}}$$与直线$${{A}{C}}$$垂直
B.存在某个位置,使得直线$${{A}{B}}$$与直线$${{C}{D}}$$垂直
C.存在某个位置,使得直线$${{B}{C}}$$与直线$${{A}{D}}$$垂直
D.对任意位置,直线$${{A}{C}}$$与$$B D, \ C D$$与$$A B, ~ A D$$与$${{B}{C}}$$均不垂直
3、['空间中直线与直线的位置关系', '异面直线垂直', '异面直线所成的角']正确率60.0%在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱中,与直线$${{B}{{A}_{1}}}$$垂直的棱所在直线的条数为()
A
A.$${{4}}$$
B.$${{5}}$$
C.$${{6}}$$
D.$${{7}}$$
4、['异面直线垂直']正确率60.0%在长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的十二条棱中,与面对角线$${{A}{C}}$$垂直且异面的棱的条数是()
A
A.$${{2}}$$
B.$${{4}}$$
C.$${{6}}$$
D.$${{8}}$$
5、['异面直线垂直', '异面直线所成的角']正确率60.0%如图所示,在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,已知$${{M}{,}{N}}$$分别是$${{B}{D}}$$和$${{A}{D}}$$上靠近$${{D}}$$点的三等分点,则$${{C}_{1}{M}}$$与$${{D}_{1}{N}}$$所成角的余弦值为()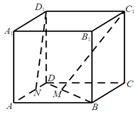
C
A.$$\frac{\sqrt{3 5}} {1 5}$$
B.$$\frac{\sqrt{1 5}} {7}$$
C.$$\frac{\sqrt{3 5}} {7}$$
D.$$\frac{\sqrt{1 5}} {1 5}$$
6、['异面直线垂直', '平行关系的综合应用']正确率60.0%若空间中三条不同的直线$$\l_{1}, ~ \l_{2}, ~ \l_{3}$$满足$$l_{1} \perp l_{2}, \ l_{2} / \! / l_{3} \,,$$则下列结论一定正确的是()
A
A.$${{l}_{1}{⊥}{{l}_{3}}}$$
B.$$l_{1} / / l_{3}$$
C.$${{l}_{1}}$$与$${{l}_{3}}$$既不平行也不垂直
D.$${{l}_{1}}$$与$${{l}_{3}}$$相交且垂直
7、['异面直线垂直', '异面直线所成的角']正确率40.0%正方体$$A B C D \!-\! A_{1} B_{1} C_{1} D_{1}$$中,$${{M}}$$为$${{D}{{D}_{1}}}$$中点,直线$${{A}{M}}$$与$${{D}_{1}{B}}$$成角余弦值为()
C
A.$$\frac{3 \sqrt{1 0}} {1 0}$$
B.$$- \frac{3 \sqrt{1 0}} {1 0}$$
C.$$\frac{\sqrt{1 5}} {5}$$
D.$$- ~ \frac{\sqrt{1 5}} {5}$$
8、['异面直线垂直', '异面直线所成的角']正确率60.0%如图,正方体$$A B C D-A^{\prime} B^{\prime} C^{\prime} D^{\prime}$$中,$${{E}}$$是棱$${{B}{C}}$$的中点,$${{G}}$$是棱$${{D}{{D}^{′}}}$$的中点,则异面直线$${{G}{B}}$$与$${{B}^{′}{E}}$$所成的角为()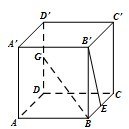
B
A.$${{1}{2}{0}^{∘}}$$
B.$${{9}{0}^{∘}}$$
C.$${{6}{0}^{∘}}$$
D.$${{3}{0}^{∘}}$$
9、['异面直线垂直', '异面直线所成的角', '立体几何中的折叠问题', '直线与平面垂直的判定定理']正确率40.0%如图,正方形$${{S}{{G}_{1}}{{G}_{2}}{{G}_{3}}}$$中,$${{E}{,}{F}}$$分别是$$G_{1} G_{2}, ~ G_{2} G_{3}$$中点,$${{D}}$$是$${{E}{F}}$$与$${{S}{{G}_{2}}}$$的交点,现沿$$S E, ~ S F$$及$${{E}{F}}$$把这个正方形折成一个四面体,使$$G_{1}, ~ G_{2}, ~ G_{3}$$三点重合,重合后的点记为$${{G}}$$,则在四面体$$G-S E F$$中必有$${{(}{)}}$$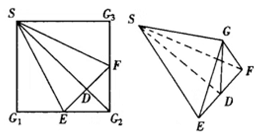
B
A.$${{S}{D}{⊥}}$$平面$${{E}{F}{G}}$$
B.$$S E \perp G F$$
C.$${{E}{F}{⊥}}$$平面$${{S}{E}{G}}$$
D.$$S E \perp S F$$
10、['异面直线垂直', '异面直线所成的角', '二面角', '直线与平面所成的角']正确率60.0%在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,下列几种说法正确的是$${{(}{)}}$$
D
A.$$A_{1} C_{1} \bot A D$$
B.直线$${{A}{{C}_{1}}}$$与平面$${{A}{B}{C}{D}}$$所成角正弦值为$$\frac{\sqrt2} {2}$$
C.二面角$$C_{1}-A B-D$$为$${{3}{0}^{0}}$$
D.$${{A}_{1}{B}}$$与$${{B}_{1}{C}}$$成$${{6}{0}^{∘}}$$角
1. 解析:
选项C错误。$$A C_1$$与$$C D$$的夹角为$$90^\circ$$,而非$$45^\circ$$。因为$$C D$$在底面$$A B C D$$上,而$$A C_1$$是空间对角线,两者不共面,夹角需要通过向量计算确定。
2. 解析:
选项B正确。在翻折过程中,当$$A B$$与$$C D$$垂直时,可以通过几何构造验证其成立。其他选项无法在所有位置满足垂直条件。
3. 解析:
选项A正确。与$$B A_1$$垂直的棱有$$A D$$、$$B C$$、$$A_1 D_1$$、$$B_1 C_1$$,共4条。
4. 解析:
选项B正确。与$$A C$$垂直且异面的棱有$$B_1 B$$、$$D_1 D$$、$$A_1 A$$、$$C_1 C$$,共4条。
5. 解析:
选项C正确。通过坐标系法计算$$C_1 M$$与$$D_1 N$$的夹角余弦值为$$\frac{\sqrt{35}}{7}$$。
6. 解析:
选项A正确。由$$l_1 \perp l_2$$且$$l_2 \parallel l_3$$,可得$$l_1 \perp l_3$$。
7. 解析:
选项A正确。通过向量法计算$$A M$$与$$D_1 B$$的夹角余弦值为$$\frac{3 \sqrt{10}}{10}$$。
8. 解析:
选项B正确。通过坐标系法验证$$G B$$与$$B' E$$垂直,夹角为$$90^\circ$$。
9. 解析:
选项D正确。在四面体$$G-S E F$$中,$$S E$$与$$S F$$垂直,因为折叠后$$S E$$和$$S F$$分别对应原正方形的两条垂直边。
10. 解析:
选项D正确。$$A_1 B$$与$$B_1 C$$的夹角为$$60^\circ$$,可通过向量计算或几何构造验证。
.jpg)