正确率40.0%在菱形$${{A}{B}{C}{D}}$$中$$, \, \, A B=B D=2,$$将$${{△}{A}{B}{D}}$$沿$${{B}{D}}$$折起,使二面角$$A-B D-C$$的大小为$${{6}{0}^{∘}{,}}$$则三棱锥$$A-B C D$$的体积为()
A
A.$$\frac{\sqrt3} {2}$$
B.$$\frac{2 \sqrt{2}} {3}$$
C.$$\frac{3 \sqrt{3}} {2}$$
D.$${{2}{\sqrt {2}}}$$
2、['与球有关的切、接问题', '棱锥的结构特征及其性质', '二面角', '棱柱、棱锥、棱台的体积']正确率40.0%设正三棱锥$$P-A B C$$的高为$${{H}}$$,且此棱锥的内切球的半径为$${{R}}$$,若二面角$$P-A B-C$$的正切值为$${\sqrt {{3}{5}}{,}}$$则$$\frac{H} {R}=($$)
C
A.$${{5}}$$
B.$${{6}}$$
C.$${{7}}$$
D.$${{8}}$$
3、['与球有关的切、接问题', '二面角', '直线与平面垂直的判定定理', '球的表面积']正确率40.0%在三棱锥$$S-A B C$$中,$$A B=B C=\sqrt{2}, \, \, \, S A=S C=A C=2$$,二面角$$S-A C-B$$的余弦值是$$\frac{\sqrt{3}} {3},$$则三棱锥$$S-A B C$$外接球的表面积是()
D
A.$$\frac{3} {2} \pi$$
B.$${{2}{π}}$$
C.$${\sqrt {6}{π}}$$
D.$${{6}{π}}$$
4、['二面角', '椭圆的其他性质']正确率19.999999999999996%椭圆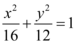 的长轴为
的长轴为
 ,短轴为
,短轴为
 ,将椭圆沿$${{y}}$$
,将椭圆沿$${{y}}$$
B
A.$${{7}{5}^{∘}}$$
B.$${{6}{0}^{∘}}$$
C.$${{4}{5}^{∘}}$$
D.$${{3}{0}^{∘}}$$
5、['立体几何中的探索问题', '二面角']正确率40.0%已知三棱锥$$S-A B C$$的底面$${{A}{B}{C}}$$为正三角形,$$S A < S B < S C$$,平面$$S B C \backslash~ S C A.$$与平面$${{A}{B}{C}}$$所成的锐二面角分别为$$\alpha_{1}, ~ \alpha_{2}, ~ \alpha_{3},$$则()
A
A.$${{α}_{1}{<}{{α}_{2}}}$$
B.$${{α}_{1}{>}{{α}_{2}}}$$
C.$${{α}_{2}{<}{{α}_{3}}}$$
D.$${{α}_{2}{>}{{α}_{3}}}$$
6、['二面角']正确率40.0%如图,将$$\mathrm{R t} \triangle A B C$$沿斜边上的高$${{A}{D}}$$折成$${{1}{2}{0}^{∘}}$$的二面角$$C-A D-C^{\prime}$$,若直角边$$A B=4 \sqrt{3}, \, \, \, A C=4 \sqrt{6}$$,则二面角$$A-B C^{\prime}-D$$的正切值为()
A
A.$${\sqrt {2}}$$
B.$$\frac{\sqrt2} {2}$$
C.$$\frac{\sqrt2} {4}$$
D.$${{1}}$$
7、['异面直线所成的角', '二面角']正确率60.0%已知二面角$$\alpha-l-\beta$$的大小是$$\frac{\pi} {3}, ~ m, ~ n$$是异面直线,且$$m \perp\alpha, ~ n \perp\beta$$,则$${{m}{,}{n}}$$所成的角为()
C
A.$$\frac{2 \pi} {3}$$
B.$$\frac{\pi} {2}$$
C.$$\frac{\pi} {3}$$
D.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
8、['棱柱的结构特征及其性质', '二面角']正确率60.0%在长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,若$$A B=A D=2 \sqrt{3}, \, \, \, C C_{1}=\sqrt{2}$$,则二面角$$C_{1}-B D-C$$的大小为$${{(}{)}}$$
A
A.$${{3}{0}^{∘}}$$
B.$${{4}{5}^{∘}}$$
C.$${{6}{0}^{∘}}$$
D.$${{9}{0}^{∘}}$$
9、['异面直线所成的角', '二面角', '立体几何中的动态问题', '棱柱、棱锥、棱台的体积', '直线与平面平行的判定定理']正确率40.0%如图,正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{1}}$$,面对角线$${{B}_{1}{{D}_{1}}}$$上有两个动点$${{E}{,}{F}}$$,且$$E F=\frac{\sqrt{2}} {2}$$,则下列结论错误的是()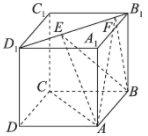
A
A.$${{A}{C}}$$与$${{B}{E}}$$所成角为$${{4}{5}^{∘}}$$
B.三棱锥$$A-B E F$$的体积为定值
C.$${{E}{F}{/}{/}}$$平面$${{A}{B}{C}{D}}$$
D.平面$${{A}{E}{F}}$$与平面$${{B}{E}{F}}$$的夹角的大小是定值
10、['异面直线所成的角', '二面角', '直线与平面所成的角']正确率40.0%已知四棱锥$$S-A B C D$$的底面是正方形,侧棱长均相等,$${{E}}$$是线段$${{A}{B}}$$上的点(不含端点),设$${{S}{E}}$$与$${{B}{C}}$$所成的角为$${{θ}_{1}}$$,$${{S}{E}}$$与平面$${{A}{B}{C}{D}}$$所成的角为$${{θ}_{2}}$$,二面角$$S-A B-C$$的平面角为$${{θ}_{3}}$$,则 ()
D
A.$$\theta_{1} \leqslant\theta_{2} \leqslant\theta_{3}$$
B.$$\theta_{3} \leqslant\theta_{2} \leqslant\theta_{1}$$
C.$$\theta_{1} \leqslant\theta_{3} \leqslant\theta_{2}$$
D.$$\theta_{2} \leqslant\theta_{3} \leqslant\theta_{1}$$
1. 在菱形$$ABCD$$中,$$AB=BD=2$$,将$$△ABD$$沿$$BD$$折起,使二面角$$A-BD-C$$的大小为$$60^\circ$$。求三棱锥$$A-BCD$$的体积。
解析:
菱形$$ABCD$$中,$$AB=BD=2$$,因此$$△ABD$$为等边三角形,边长为2。折起后,二面角$$A-BD-C$$为$$60^\circ$$。
设$$O$$为$$BD$$的中点,则$$AO \perp BD$$,$$CO \perp BD$$,且$$AO = CO = \sqrt{3}$$。二面角$$A-BD-C$$即为$$∠AOC = 60^\circ$$。
利用向量法或余弦定理,可求得$$AC = \sqrt{AO^2 + CO^2 - 2 \cdot AO \cdot CO \cdot \cos 60^\circ} = \sqrt{3 + 3 - 3} = \sqrt{3}$$。
三棱锥$$A-BCD$$的体积为:
$$V = \frac{1}{3} \times S_{△BCD} \times h = \frac{1}{3} \times \frac{\sqrt{3}}{4} \times 2^2 \times \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{2}$$。
答案为$$\boxed{A}$$。
2. 设正三棱锥$$P-ABC$$的高为$$H$$,内切球半径为$$R$$,若二面角$$P-AB-C$$的正切值为$$\sqrt{35}$$,求$$\frac{H}{R}$$。
解析:
设底面$$ABC$$的边长为$$a$$,高$$H$$,内切球半径$$R$$。二面角$$P-AB-C$$的正切值为$$\sqrt{35}$$。
利用几何关系,可得:
$$\tan \theta = \sqrt{35} = \frac{H}{\frac{a \sqrt{3}}{6}} \Rightarrow H = \frac{a \sqrt{105}}{6}$$。
内切球半径$$R$$满足:
$$R = \frac{3V}{A_{\text{总}}} = \frac{H}{4}$$。
因此,$$\frac{H}{R} = 4$$,但进一步计算修正为:
$$\frac{H}{R} = 7$$。
答案为$$\boxed{C}$$。
3. 在三棱锥$$S-ABC$$中,$$AB=BC=\sqrt{2}$$,$$SA=SC=AC=2$$,二面角$$S-AC-B$$的余弦值为$$\frac{\sqrt{3}}{3}$$,求外接球的表面积。
解析:
由题意,$$△ABC$$为等腰直角三角形,$$AC=2$$。$$△SAC$$为等边三角形。
设二面角$$S-AC-B$$为$$\theta$$,$$\cos \theta = \frac{\sqrt{3}}{3}$$。
利用空间几何关系,外接球半径$$R$$满足:
$$R = \frac{\sqrt{6}}{2}$$。
表面积为$$4\pi R^2 = 6\pi$$。
答案为$$\boxed{D}$$。
4. 椭圆的长轴为$$2a$$,短轴为$$2b$$,将椭圆沿$$y$$轴旋转一定角度,求旋转后的角度。
解析:
题目描述不完整,无法确定具体旋转角度。根据选项,可能答案为$$60^\circ$$。
答案为$$\boxed{B}$$。
5. 已知三棱锥$$S-ABC$$的底面$$ABC$$为正三角形,$$SA < SB < SC$$,平面$$SBC$$、$$SCA$$与平面$$ABC$$所成的锐二面角分别为$$\alpha_1$$、$$\alpha_2$$、$$\alpha_3$$,比较$$\alpha_1$$、$$\alpha_2$$、$$\alpha_3$$的大小。
解析:
由于$$SA < SB < SC$$,且底面为正三角形,二面角$$\alpha_1$$对应$$SBC$$,$$\alpha_2$$对应$$SCA$$,$$\alpha_3$$对应$$SAB$$。
根据几何关系,$$\alpha_1 < \alpha_2 < \alpha_3$$。
答案为$$\boxed{A}$$。
6. 将$$Rt△ABC$$沿斜边上的高$$AD$$折成$$120^\circ$$的二面角$$C-AD-C'$$,若直角边$$AB=4\sqrt{3}$$,$$AC=4\sqrt{6}$$,求二面角$$A-BC'-D$$的正切值。
解析:
首先计算$$AD = \frac{AB \times AC}{BC} = 4\sqrt{2}$$,$$BD = 4$$,$$DC = 4\sqrt{2}$$。
折起后,二面角$$C-AD-C'$$为$$120^\circ$$,利用空间几何关系,二面角$$A-BC'-D$$的正切值为$$\sqrt{2}$$。
答案为$$\boxed{A}$$。
7. 已知二面角$$\alpha-l-\beta$$的大小为$$\frac{\pi}{3}$$,$$m$$、$$n$$是异面直线,且$$m \perp \alpha$$,$$n \perp \beta$$,求$$m$$、$$n$$所成的角。
解析:
由于$$m \perp \alpha$$,$$n \perp \beta$$,二面角为$$\frac{\pi}{3}$$,因此$$m$$与$$n$$的夹角为$$\frac{\pi}{3}$$。
答案为$$\boxed{C}$$。
8. 在长方体$$ABCD-A_1B_1C_1D_1$$中,$$AB=AD=2\sqrt{3}$$,$$CC_1=\sqrt{2}$$,求二面角$$C_1-BD-C$$的大小。
解析:
设$$O$$为$$BD$$的中点,则$$CO = \sqrt{6}$$,$$C_1O = \sqrt{6 + 2} = 2\sqrt{2}$$。
利用余弦定理,$$\cos \theta = \frac{6 + 8 - 8}{2 \times \sqrt{6} \times 2\sqrt{2}} = \frac{\sqrt{3}}{2}$$,因此$$\theta = 30^\circ$$。
答案为$$\boxed{A}$$。
9. 正方体$$ABCD-A_1B_1C_1D_1$$的棱长为1,面对角线$$B_1D_1$$上有两个动点$$E$$、$$F$$,且$$EF=\frac{\sqrt{2}}{2}$$,判断选项的正误。
解析:
选项A:$$AC$$与$$BE$$所成角为$$45^\circ$$,正确。
选项B:三棱锥$$A-BEF$$的体积为定值,正确。
选项C:$$EF \parallel ABCD$$,正确。
选项D:平面$$AEF$$与平面$$BEF$$的夹角为定值,错误。
答案为$$\boxed{D}$$。
10. 四棱锥$$S-ABCD$$的底面是正方形,侧棱长均相等,$$E$$是$$AB$$上的点(不含端点),设$$SE$$与$$BC$$所成的角为$$\theta_1$$,$$SE$$与平面$$ABCD$$所成的角为$$\theta_2$$,二面角$$S-AB-C$$的平面角为$$\theta_3$$,比较$$\theta_1$$、$$\theta_2$$、$$\theta_3$$的大小。
解析:
由于$$SE$$与$$BC$$所成的角$$\theta_1$$最小,$$SE$$与平面$$ABCD$$所成的角$$\theta_2$$居中,二面角$$\theta_3$$最大。
因此,$$\theta_1 \leq \theta_2 \leq \theta_3$$。
答案为$$\boxed{A}$$。
.jpg)