平面与平面平行的判定定理-8.5 空间直线、平面的平行知识点回顾进阶单选题自测题解析-四川省等高二数学必修,平均正确率52.0%

1、['充分、必要条件的判定'， '平面与平面平行的判定定理']

正确率40.0%已知$$m， ~ n， ~ l_{1}， ~ l_{2}$$表示直线$${，{α}{，}{β}}$$表示平面，若$$m \subset\alpha， n$$$$\subset\alpha， l_{1} \subset\beta， l_{2} \subset\beta， l_{1} \cap l_{2}=M，$$则$${{α}{/}{/}{β}}$$的一个充分条件是（）

A.$${{m}{/}{/}{β}}$$且$$l_{1} / / \alpha$$

B.$${{m}{/}{/}{β}}$$且$${{n}{/}{/}{β}}$$

C.$${{m}{/}{/}{β}}$$且$${{n}{/}{/}{{l}_{2}}}$$

D.$${{m}{/}{/}{{l}_{1}}}$$且$${{n}{/}{/}{{l}_{2}}}$$

2、['余弦定理及其应用'， '异面直线所成的角'， '平面与平面平行的性质定理'， '平面与平面平行的判定定理']

正确率40.0%在正三棱柱$$A B C-A_{1} B_{1} C_{1}$$中，$$A_{1} A=2 A B=2$$，平面$${{α}}$$过定点$${{A}}$$，平面$${{α}{/}{/}}$$平面$${{A}_{1}{B}{C}}$$，面$${{α}{∩}}$$平面$$A B C=m$$，面$${{α}{∩}}$$平面$$A_{1} C_{1} C=n$$，则$${{m}{，}{n}}$$所成角的余弦值为（）

A.$$\frac{\sqrt{5}} {1 0}$$

B.$$\frac{\sqrt2} {2}$$

C.$$\frac{3} {5}$$

D.$$\frac{1} {3}$$

3、['空间中直线与平面的位置关系'， '空间中平面与平面的位置关系'， '平面与平面平行的判定定理']

正确率40.0%若$${{α}}$$，$${{β}}$$，$${{γ}}$$表示三个不同的平面，$${{l}}$$表示直线，则下列条件能推出$${{α}{/}{/}{β}}$$的是$${{(}{)}}$$

A.$${{l}{⊂}{α}}$$，$${{l}{/}{/}{β}}$$

B.$${{l}{/}{/}{α}}$$，$${{l}{/}{/}{β}}$$

C.$${{l}{⊥}{α}}$$，$${{l}{⊥}{β}}$$

D.$${{α}{⊥}{γ}}$$，$${{β}{⊥}{γ}}$$

4、['平面'， '平面与平面平行的判定定理']

正确率80.0%在立体几何中，用一个平面去截一个几何体得到的平面图形叫截面，如图，在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，点$${{E}}$$、$${{F}}$$分别是棱$${{B}_{1}{B}}$$、$${{B}_{1}{{C}_{1}}}$$的中点，点$${{G}}$$是棱$${{C}{{C}_{1}}}$$的中点，则过线段$${{A}{G}}$$且平行于平面$${{A}_{1}{E}{F}}$$的截面图形为$${{(}{)}}$$

A.矩形

B.三角形

C.正方形

D.等腰梯形

5、['平面与平面平行的判定定理']

正确率60.0%平面$${{α}}$$与平面$${{β}}$$平行的条件可以是$${{(}{)}}$$

A.$${{α}}$$内有无数多条直线都与$${{β}}$$平行

B.直线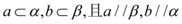

C.直线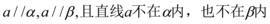

D.一个平面$${{α}}$$内两条不平行的直线都平行于另一个平面$${{β}}$$

6、['直线与平面垂直的性质定理'， '直线与平面平行的判定定理'， '平面与平面平行的判定定理']

正确率60.0%已知三条不重合的直线$$m， ~ n， ~ l$$，两个不重合的平面$${{α}{，}{β}{，}}$$以下命题中真命题是（）
$${①}$$若$$m \left/ \! / n， n \right. \subset\alpha$$，则 $\text{[math]}$ 若$$l \bot\alpha， m \bot\beta$$且$${{m}{/}{/}{l}}$$，则$$\alpha\， / / \beta;$$若$$m \subset a， n \subset a， m / / \beta， n / / \beta$$，则$$\alpha\， / / \beta;$$$${④}$$若$$a \perp\beta， a \cap\beta=m， n， \subset\beta， n \perp m$$则$${{n}{⊥}{α}}$$．

A.$${①{②}}$$

B.$${②{④}}$$

C.$${①{③}}$$

D.$${③{④}}$$

7、['空间中直线与直线的位置关系'， '直线与平面垂直的判定定理'， '直线与平面垂直的性质定理'， '平面与平面平行的性质定理'， '平面与平面平行的判定定理']

正确率40.0%若$${{m}{，}{n}}$$是两条不同的直线，$$\alpha， \beta， \gamma$$是三个不同的平面： $\text{[math]}$ 若$$\alpha\bigcap\gamma=m， \beta\bigcap\gamma=n， \， \， \， m / / n，$$则$$\alpha/ / \beta，$$则以上说法中正确的有$${{(}{)}}$$个

A.$${{1}}$$

B.$${{2}}$$

C.$${{3}}$$

D.$${{4}}$$

8、['平面与平面平行的判定定理']

正确率60.0%平面$${{α}}$$与平面$${{β}}$$平行的条件可以是（）

A.$${{α}}$$内有无穷多条直线与$${{β}}$$平行

B.直线$$a / / \alpha， ~ a / / \beta$$

C.直线$${{a}{⊂}{α}}$$，直线$${{b}{⊂}{β}}$$，且$$a / / \beta， ~ b / / \alpha$$

D.$${{α}}$$内的任何直线都与$${{β}}$$平行

9、['空间中直线与直线的位置关系'， '立体几何位置关系的综合应用'， '空间中直线与平面的位置关系'， '空间中平面与平面的位置关系'， '基本事实3'， '直线与平面垂直的性质定理'， '命题的真假性判断'， '平面与平面平行的判定定理']

正确率60.0%下列命题中，正确的命题是（）

A.任意三点确定一个平面

B.三条平行直线最多确定一个平面

C.不同的两条直线均垂直于同一个平面，则这两条直线平行

D.一个平面中的两条直线与另一个平面都平行，则这两个平面平行

10、['平面与平面平行的判定定理']

正确率40.0%平面α∥平面β的一个充分条件是（　　）

A.存在一条直线a，a∥α，a∥β

B.存在一条直线a，a⊂α，a∥β

C.存在两条平行直线a，b，a⊂α，b⊂β，a∥β，b∥α

D.存在两条异面直线a，b，a⊂α，b⊂β，a∥β，b∥α

1、解析：

要证明平面$$α$$平行于平面$$β$$，需要满足两个平面内的两条相交直线分别平行。选项D中，$$m \parallel l_1$$且$$n \parallel l_2$$，由于$$l_1$$和$$l_2$$相交于$$M$$，因此$$α$$内的两条直线$$m$$和$$n$$分别平行于$$β$$内的两条相交直线，满足充分条件。其他选项均不满足两条相交直线平行的条件。

正确答案：D

2、解析：

首先确定平面$$α$$与平面$$A_1BC$$平行，且过点$$A$$。由于$$α \parallel A_1BC$$，交线$$m$$在底面$$ABC$$内且平行于$$BC$$。交线$$n$$在侧面$$A_1C_1C$$内，且平行于$$A_1C$$。计算$$m$$和$$n$$的方向向量分别为$$\vec{BC}$$和$$\vec{A_1C}$$，利用向量夹角公式可得余弦值为$$\frac{\sqrt{5}}{10}$$。

正确答案：A

3、解析：

选项C中，$$l \perp α$$且$$l \perp β$$，说明$$α$$和$$β$$的法向量平行，因此$$α \parallel β$$。选项A和B中，直线平行于平面并不足以推出平面平行；选项D中，两平面垂直于同一平面也不一定平行。

正确答案：C

4、解析：

通过几何分析，过$$AG$$且平行于平面$$A_1EF$$的截面与正方体的交线形成一个四边形。由于$$AG$$与$$A_1EF$$的平行关系，截面图形为等腰梯形。

正确答案：D

5、解析：

选项D中，$$α$$内两条不平行的直线都平行于$$β$$，说明$$α$$与$$β$$无交点，因此平行。选项A中，无数条直线平行并不充分；选项B和C的条件不足以保证平面平行。

正确答案：D

6、解析：

命题①错误，因为$$m \parallel n$$且$$n \subset α$$并不能推出$$m \parallel α$$；命题②正确，因为$$l \perp α$$且$$m \parallel l$$推出$$m \perp α$$，结合$$m \perp β$$可得$$α \parallel β$$；命题③错误，因为$$m$$和$$n$$需相交才能推出$$α \parallel β$$；命题④正确，符合面面垂直的性质定理。

正确答案：B

7、解析：

命题①错误，$$m \parallel α$$且$$n \parallel α$$不能推出$$m \parallel n$$；命题②正确，垂直于同一平面的两直线平行；命题③错误，$$α \cap γ = m$$且$$β \cap γ = n$$且$$m \parallel n$$不能推出$$α \parallel β$$；命题④错误，缺少相交条件。因此仅命题②正确。

正确答案：A

8、解析：

选项D正确，因为$$α$$内任何直线都与$$β$$平行，说明$$α$$与$$β$$无交点。选项A不充分，因为无穷多条直线可能平行但不共面；选项B和C的条件不足以保证平面平行。

正确答案：D

9、解析：

选项A错误，三点共线时不能确定平面；选项B错误，三条平行直线可确定三个平面；选项C正确，垂直于同一平面的两直线平行；选项D错误，需两直线相交才能推出平面平行。

正确答案：C

10、解析：

选项D正确，因为两条异面直线分别平行于另一平面，说明两平面无交点。选项A和B的条件不足；选项C中平行直线可能共面，不充分。

正确答案：D

_{题目来源于各渠道收集，若侵权请联系下方邮箱}