正确率60.0%如图,在三棱柱$$A B C-A_{1} B_{1} C_{1}$$中,过$$A_{1}, ~ B, ~ C_{1}$$的平面与平面$${{A}{B}{C}}$$相交于$${{l}{,}}$$则()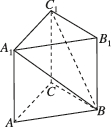
A
A.$$\l/ A C$$
B.$${{l}}$$与$${{A}{C}}$$相交
C.$${{l}}$$与$${{A}{C}}$$异面
D.以上均不正确
2、['直线与平面平行的性质定理']正确率60.0%如图,在三棱柱$$A B C-A_{1} B_{1} C_{1}$$中,$${{M}{,}{N}}$$分别为棱$$A A_{1}, ~ B B_{1}$$的中点,过$${{M}{N}}$$作一个平面分别交底面三角形$${{A}{B}{C}}$$的边$$B C, ~ A C$$于点$${{E}{,}{F}{,}}$$则()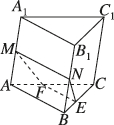
B
A.$$M F / / N E$$
B.四边形$${{M}{N}{E}{F}}$$为梯形
C.四边形$${{M}{N}{E}{F}}$$为平行四边形
D.$$A_{1} B_{1} / \! / N E$$
3、['直线与平面垂直的性质定理', '直线与平面平行的性质定理']正确率60.0%已知互相垂直的平面$${{α}}$$,$${{β}}$$交于直线$${{l}{.}}$$若直线$${{m}}$$,$${{n}}$$满足$${{m}{/}{/}{α}}$$,$${{n}{⊥}{β}}$$,则()
C
A.$${{m}{/}{/}{l}}$$
B.$${{m}{/}{/}{n}}$$
C.$${{n}{⊥}{l}}$$
D.$${{m}{⊥}{n}}$$
4、['空间中直线与平面的位置关系', '异面直线垂直', '点到平面的距离', '直线与平面平行的性质定理']正确率80.0%若直线$${{a}}$$平行于平面$${{α}}$$,则下列结论错误的是()
A
A.$${{a}}$$平行于$${{α}}$$内的所有直线
B.$${{α}}$$内有无数条直线与$${{a}}$$平行
C.直线$${{a}}$$上的点到平面$${{α}}$$的距离相等
D.$${{α}}$$内存在无数条直线与$${{a}}$$成$${{9}{0}{°}}$$角
5、['空间中直线与直线的位置关系', '直线与平面垂直的性质定理', '平面与平面垂直的性质定理', '直线与平面平行的判定定理', '直线与平面平行的性质定理']正确率60.0%已知$${{m}{,}{n}}$$为两条不同的直线,$${{α}{,}{β}}$$为两个不同的平面,则下列命题正确的是()
C
A.若$$m \perp n, n \perp$$
B.若$$m / / \alpha, n / \! / \alpha$$
C.若$$m \perp\alpha, n \perp$$
D.若$$\alpha\perp\beta, n / / \beta, \mathbb{T} n / \! / \alpha$$
6、['基本事实4', '直线与平面平行的性质定理']正确率60.0%如图,在长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中$${,{E}{,}{F}}$$分别是棱$${{A}{{A}_{1}}}$$和$${{B}{{B}_{1}}}$$的中点,过$${{E}{F}}$$的平面$${{E}{F}{G}{H}}$$分别交$$B C, ~ A D$$于点$${{G}{,}{H}{,}}$$则$${{G}{H}}$$与$${{A}{B}}$$的位置关系是()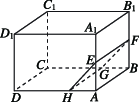
A
A.平行
B.相交
C.异面
D.不确定
7、['空间中直线与平面的位置关系', '直线与平面平行的性质定理', '平面与平面平行的判定定理']正确率40.0%已知$${{m}{,}{n}}$$是两条直线,$${{α}{,}{β}}$$是两个平面,则下列命题中正确的是$${{(}{)}}$$
D
A.$$m \perp\alpha, \, \, \, \alpha\perp\beta, \, \, \, m / \! / n \Rightarrow n / \! / \beta$$
B.$$m / / \alpha, \, \, \, \alpha\cap\beta=n \Rightarrow n / / m$$
C.$$\alpha/ / \beta, \, \, m / / \alpha, \, \, m \perp n \Rightarrow n \perp\beta$$
D.$$m \perp\alpha, \, \, n \perp\beta, \, \, m / \! / n \Rightarrow\alpha/ \! / \beta$$
8、['立体几何中的截面、交线问题', '直线与平面平行的性质定理', '立体几何中的轨迹问题']正确率40.0%已知正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{1}{,}{E}}$$是棱$${{D}_{1}{{C}_{1}}}$$的中点,点$${{F}}$$在正方体内部或正方体的表面上,且$${{E}{F}{/}{/}}$$平面$${{A}_{1}{B}{{C}_{1}}}$$,则动点$${{F}}$$的轨迹所形成的区域面积是()
C
A.$$\begin{array} {l l} {\underset{\frac{9} {8}}} \\ \end{array}$$
B.$$\frac{\sqrt3} {2}$$
C.$$\frac{3 \sqrt{3}} {4}$$
D.$${\sqrt {2}}$$
9、['立体几何中的截面、交线问题', '直线与平面所成的角', '直线与平面平行的判定定理', '直线与平面平行的性质定理']正确率40.0%如图,已知圆锥的顶点为$${{S}}$$,底面圆$${{O}}$$的两条直径分别为$${{A}{B}}$$和$${{C}{D}}$$,且$$A B \perp C D$$,若平面$${{S}{A}{D}{∩}}$$平面$$S B C=l.$$现有以下四个结论: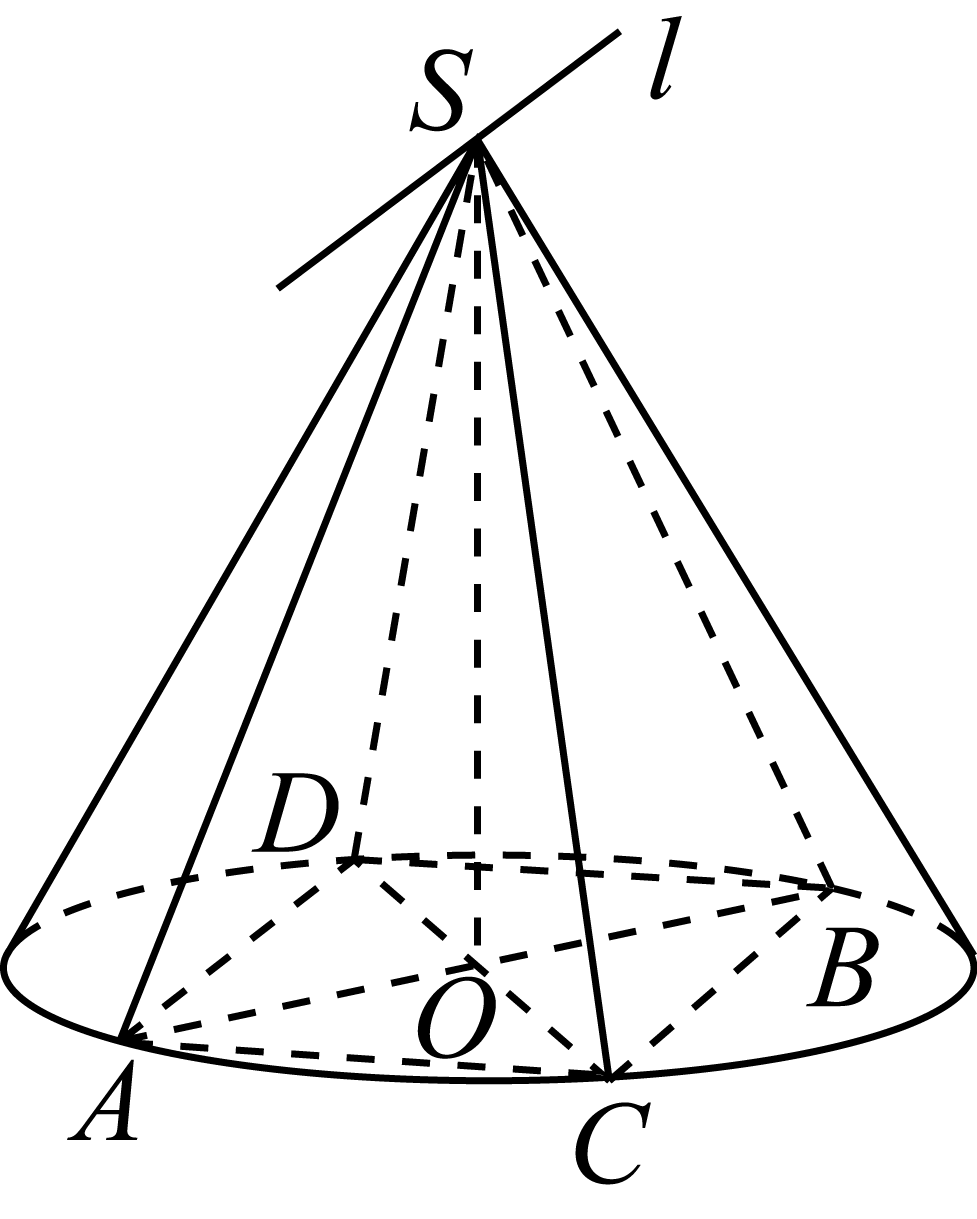
$$\oplus\, A D / /$$平面$${{S}{B}{C}}$$;
$$\odot\, \, \l/ / A D$$;
$${③{l}}$$与平面$${{S}{C}{D}}$$所成的角为$${{6}{0}{^{∘}}}$$;
$${④}$$若$${{E}}$$是底面圆周上的动点,则$${{△}{S}{A}{E}}$$的最大面积等于$${{△}{S}{A}{B}}$$的面积.
其中正确结论的个数是()
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
10、['空间中直线与平面的位置关系', '直线与平面垂直的性质定理', '直线与平面平行的性质定理']正确率60.0%已知平面$${{α}{⊥}}$$平面$$\beta, \, \, \, \alpha\cap\beta=l,$$点$$A \in\alpha, \ A \notin l,$$直线$$A B / / l,$$直线$$A C \perp l,$$直线$$m / / \alpha, ~ m / / \beta,$$则下列四种位置关系中,不一定成立的是()
D
A.$$A B / / m$$
B.$${{A}{C}{⊥}{m}}$$
C.$$A B / / \beta$$
D.$${{A}{C}{⊥}{β}}$$
1. 解析:在三棱柱$$ABC-A_1B_1C_1$$中,平面$$A_1BC_1$$与平面$$ABC$$的交线$$l$$平行于$$A_1C_1$$和$$AC$$,因为$$A_1C_1 \parallel AC$$。因此,$$l \parallel AC$$,选项A正确。
3. 解析:平面$$α$$和$$β$$互相垂直且交于直线$$l$$。若$$m \parallel α$$且$$n \perp β$$,则$$n$$垂直于$$β$$内的所有直线,包括$$l$$,因此$$n \perp l$$,选项C正确。
5. 解析:选项D正确,因为若$$α \perp β$$且$$n \parallel β$$,则$$n$$可能与$$α$$平行或在$$α$$内,但题目未明确$$n$$是否在$$α$$内,因此$$n \parallel α$$不一定成立。其他选项A、B、C的表述不完整或错误。
7. 解析:选项D正确,因为若$$m \perp α$$且$$n \perp β$$,且$$m \parallel n$$,则平面$$α$$和$$β$$的法向量平行,因此$$α \parallel β$$。其他选项A、B、C的推理不成立。
9. 解析:圆锥的底面圆$$O$$中,$$AB \perp CD$$,且平面$$SAD$$与平面$$SBC$$的交线$$l \parallel AD$$(因为$$AD \parallel BC$$)。$$AD \parallel$$平面$$SBC$$,$$l$$与平面$$SCD$$所成的角为$$60^\circ$$,且$$△SAE$$的最大面积等于$$△SAB$$的面积。因此四个结论均正确,选项D正确。
.jpg)