.jpg)
正确率60.0%在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，$${{A}{C}}$$与$${{B}{D}}$$的交点为$${{O}{，}}$$关于直线$${{A}_{1}{O}{，}}$$下列说法正确的是（）
B
A.$$A_{1} O / / D_{1} C$$
B.$$A_{1} O / \! /$$平面$${{B}_{1}{C}{{D}_{1}}}$$
C.$$A_{1} O \perp B C$$
D.$${{A}_{1}{O}{⊥}}$$平面$${{A}{{B}_{1}}{{D}_{1}}}$$
2、['空间中直线与平面的位置关系'， '直线与平面平行的判定定理'， '平面与平面平行的判定定理']正确率40.0%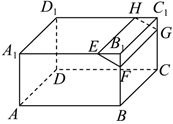
如图，在长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，$${\frac{A_{1} E} {E B_{1}}}={\frac{B F} {F B_{1}}}={\frac{C G} {G C_{1}}}={\frac{D_{1} H} {H C_{1}}}=2$$，则下列说法错误的是$${{(}{)}}$$
A.$$B D_{1} / / G H$$
B.$${{B}{D}}$$与$${{E}{F}}$$异面
C.$${{E}{H}{/}{/}}$$平面$${{A}{B}{C}{D}}$$
D.平面$$E F G H / /$$平面$$A_{1} B C D_{1}$$
3、['平行关系的综合应用'， '平面与平面平行的判定定理']正确率60.0%已知$${{m}{，}{n}}$$是两条直线，$${{α}{，}{β}}$$是两个平面，有以下说法：
$${①{m}{，}{n}}$$相交且都在平面$${{α}{，}{β}}$$外，$$m / / \alpha， ~ m / / \beta， ~ n / / \alpha， ~ n / / \beta$$，则$$\alpha/ / \beta;$$
$${②}$$若$$m / / \alpha， ~ m / / \beta$$，则$$\alpha/ / \beta;$$
$${③}$$若$$m / / \alpha， ~ n / / \beta， ~ m / / n$$，则$$\alpha/ / \beta.$$
其中说法正确的个数是（）
B
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
4、['两条直线平行'， '直线与平面平行的判定定理'， '平面与平面平行的性质定理'， '直线与平面平行的性质定理'， '平面与平面平行的判定定理']正确率40.0%给出下列命题，其中正确的两个命题是$${{(}{)}}$$
$${①}$$直线上有两点到平面的距离相等，则此直线与平面平行$${②}$$夹在两个平行平面间的两条异面线段的中点连线平行于这两个平面$${③}$$直线$${{m}{⊥}}$$平面$${{α}{，}}$$直线$${{n}{⊥}{m}}$$，则$${{n}{/}{/}{α}}$$$${④{a}{、}{b}}$$是异面直线，则存在唯一的平面$${{α}{，}}$$使它与$${{a}{、}{b}}$$都平行且与$${{a}{、}{b}}$$距离相等．
D
A.$${①{②}}$$
B.$${②{③}}$$
C.$${③{④}}$$
D.$${②{④}}$$
5、['空间中直线与直线的位置关系'， '空间中直线与平面的位置关系'， '空间中平面与平面的位置关系'， '平面与平面平行的判定定理']正确率40.0%对于不重合的两平面$${{α}{，}{β}{，}}$$给定下列条件：
$${①}$$存在平面$${{γ}{，}}$$使得$${{α}{，}{β}}$$都垂直于$${{γ}{；}}$$
$${②}$$存在平面$${{γ}{，}}$$使得$${{α}{，}{β}}$$都平行于$${{γ}{；}}$$
$${③}$$存在直线$$l \subset\alpha， m \subset\beta，$$；
$${④}$$存在异面直线$$l， m$$
其中可以判定$${{α}{，}{β}}$$平行的条件有（）
B
A.$${{1}}$$个
B.$${{2}}$$个
C.$${{3}}$$个
D.$${{4}}$$个
6、['直线与平面垂直的判定定理'， '直线与平面垂直的性质定理'， '平面与平面平行的性质定理'， '平面与平面平行的判定定理']正确率40.0%已知直线$${{m}{，}{l}}$$，平面$${{α}{，}{β}{，}}$$且$$m \bot\alpha， \， \， l \subset\beta$$，给出下列命题：
$${①}$$若$$\alpha\， / / \beta，$$则$$m \bot l ; \ \textcircled{2}$$若$${{m}{⊥}{l}}$$，则$$\alpha\， / / \beta;$$若$${{α}{⊥}{β}{，}}$$则$$m \， / / l ; \， \oplus$$若$${{m}{/}{/}{l}}$$，则$${{α}{⊥}{β}{.}}$$其中正确命题的个数有（）个．
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
7、['平面与平面平行的判定定理']正确率40.0%两个平面平行的条件是$${{(}{)}}$$
D
A.一个平面内一条直线平行于另一个平面
B.一个平面内两条直线平行于另一个平面
C.一个平面内的无数条直线平行于另一个平面
D.一个平面内的任意一条直线平行于另一个平面
8、['空间中直线与平面的位置关系'， '平面与平面平行的判定定理']正确率80.0%已知$${{α}}$$，$${{β}}$$表示不同平面，则$${{α}{/}{/}{β}}$$的充分条件是$${{(}{)}}$$
D
A.存在直线$${{a}}$$，$${{b}}$$，且$${{a}}$$，$${{b}{⊂}{α}}$$，$${{a}{/}{/}{β}}$$，$${{b}{/}{/}{β}}$$
B.存在直线$${{a}}$$，$${{b}}$$，且$${{a}{⊂}{α}}$$，$${{b}{⊂}{β}}$$，$${{a}{/}{/}{β}}$$，$${{b}{/}{/}{α}}$$
C.存在平面$${{γ}}$$，$${{α}{⊥}{γ}}$$，$${{β}{⊥}{γ}}$$
D.存在直线$${{a}}$$，$${{a}{⊥}{α}}$$，$${{a}{⊥}{β}}$$
9、['立体几何中的探索问题'， '直线与平面平行的判定定理'， '平面与平面平行的判定定理']正确率0.0%如图，在棱长为$${{2}}$$的正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，$${{E}}$$，$${{F}}$$，$${{G}}$$分别是棱$${{A}{B}}$$，$${{B}{C}}$$，$${{C}{{C}_{1}}}$$的中点，$${{P}}$$是底面$${{A}{B}{C}{D}}$$内一动点．若直线$${{D}_{1}{P}}$$与平面$${{E}{F}{G}}$$不存在公共点，则三角形$${{P}{B}{{B}_{1}}}$$的面积的最小值为$${{(}{)}}$$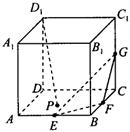
C
A.$$\frac{\sqrt2} {2}$$
B.$${{1}}$$
C.$${\sqrt {2}}$$
D.$${{2}}$$
10、['用空间向量研究距离、夹角问题'， '命题及其关系'， '多面体'， '直线与平面垂直的判定定理'， '棱柱、棱锥、棱台的表面积和体积'， '平面与平面平行的判定定理']正确率80.0%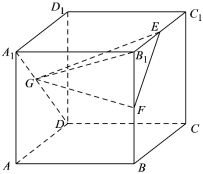
如图，在棱长为$${{2}}$$的正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，$${{E}}$$、$${{F}}$$分别为棱$${{B}_{1}{C}}$$，$${{B}{{B}_{1}}}$$的中点，$${{G}}$$为面对角线$${{A}_{1}{D}}$$上的一个动点，则下列选项中不正确的是$${{(}{)}}$$
A.三棱锥$$B_{1}-E F G$$的体积为定值
B.线段$${{A}_{1}{D}}$$上存在点$${{G}}$$，使$${{A}_{1}{C}{⊥}}$$平面$${{E}{F}{G}}$$
C.线段$${{A}_{1}{D}}$$上存在点$${{G}}$$，使平面$$E F G / /$$平面$${{A}{C}{{D}_{1}}}$$
D.设直线$${{F}{G}}$$与平面$${{A}{D}{{D}_{1}}{{A}_{1}}}$$所成角为$${{θ}}$$，则$${{s}{i}{n}{θ}}$$的最大值为$$\frac{2 \sqrt{2}} {3}$$
1. 解析：
在正方体中，$$A_1O$$是体对角线，$$D_1C$$是面对角线，两者不平行（A错误）。由于$$A_1O$$与平面$$B_1CD_1$$的法向量垂直，且$$A_1O$$不在平面内，故平行（B正确）。$$A_1O$$与$$BC$$垂直（C正确）。$$A_1O$$垂直于平面$$AB_1D_1$$（D正确）。综上，正确答案为$$B, C, D$$。
2. 解析：
根据比例关系，$$E, F, G, H$$均为各边的三等分点。$$BD_1$$与$$GH$$平行（A正确）。$$BD$$与$$EF$$异面（B正确）。$$EH$$平行于底面$$ABCD$$（C正确）。平面$$EFGH$$与平面$$A_1BCD_1$$不平行（D错误）。故错误的选项是$$D$$。
3. 解析：
①两条相交直线平行于两个平面，则两平面平行（正确）。②一条直线平行于两个平面，两平面可能相交（错误）。③两条平行直线分别平行于两个平面，两平面可能相交（错误）。故正确的个数是$$1$$（B）。
4. 解析：
①直线上两点到平面距离相等，直线可能与平面相交（错误）。②异面线段中点连线平行于两平行平面（正确）。③直线$$n$$可能平行于平面或在平面内（错误）。④存在唯一平面与异面直线平行且等距（正确）。故正确的命题是②④（D）。
5. 解析：
①两平面垂直于同一平面可能相交（错误）。②两平面平行于同一平面则平行（正确）。③存在共面直线$$l, m$$无法判定平行（错误）。④存在异面直线平行于两平面则平行（正确）。故判定条件有$$2$$个（B）。
6. 解析：
①若$$\alpha \parallel \beta$$，则$$m \perp l$$（正确）。②若$$m \perp l$$，两平面可能相交（错误）。③若$$\alpha \perp \beta$$，$$m$$与$$l$$可能相交（错误）。④若$$m \parallel l$$，则$$\alpha \perp \beta$$（正确）。故正确命题有$$2$$个（B）。
7. 解析：
两平面平行的条件是其中一个平面内任意一条直线平行于另一个平面（D）。其他选项均不充分。
8. 解析：
充分条件是存在一条直线垂直于两平面（D）。其他选项均为必要条件而非充分条件。
9. 解析：
直线$$D_1P$$与平面$$EFG$$无交点，则$$P$$在平面$$EFG$$的平行平面内。最小距离时，$$P$$到$$BB_1$$的距离为$$1$$，故面积最小值为$$1$$（B）。
10. 解析：
三棱锥体积为定值（A正确）。$$A_1C$$不垂直于平面$$EFG$$（B错误）。平面$$EFG$$与平面$$ACD_1$$不平行（C错误）。$$\sin \theta$$的最大值为$$\frac{2\sqrt{2}}{3}$$（D正确）。故不正确的是$$B, C$$。