.jpg)
正确率19.999999999999996%如图，在长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中$$， \， A D=D D_{1}=1， \， A B=\sqrt{3}， \， E， F$$分别是$$A B， B C$$上靠近$${{B}}$$点的三等分点$${，{G}}$$是$${{C}{{C}_{1}}}$$上靠近$${{C}_{1}}$$的三等分点$${，{P}}$$是底面$${{A}{B}{C}{D}}$$内的一个动点，若直线$${{D}_{1}{P}}$$与平面$${{E}{F}{G}}$$平行，则$${{△}{B}{{B}_{1}}{P}}$$周长的最小值是（）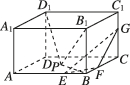
A
A.$$\frac{2+\sqrt{3}+\sqrt{7}} {2}$$
B.$${{2}{+}{\sqrt {2}}}$$
C.$${{3}{+}{\sqrt {3}}}$$
D.$$\frac{4+\sqrt{3}+\sqrt{7}} {4}$$
2、['空间中直线与平面的位置关系'， '平面与平面平行的性质定理']正确率60.0%如图，在三棱柱$$A B C-A_{1} B_{1} C_{1}$$中，$${{A}{{A}_{1}}{⊥}}$$平面$$A B C， \， \， \， A C=B C， \， \， \， M， \， \， \， N$$分别是$${{A}_{1}{{B}_{1}}}$$，$${{A}{B}}$$的中点$${，{P}}$$在线段$${{B}_{1}{C}}$$上，则$${{N}{P}}$$与平面$${{A}{M}{{C}_{1}}}$$的位置关系是（）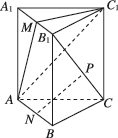
B
A.垂直
B.平行
C.相交但不垂直
D.要依$${{P}}$$点的位置而定
3、['平面与平面平行的性质定理']正确率60.0%如图，在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，若经过$${{D}_{1}{B}}$$的平面分别交$${{A}{{A}_{1}}}$$和$${{C}{{C}_{1}}}$$于点$${{E}{，}{F}{，}}$$则四边形$$D_{1} E B F$$一定是（）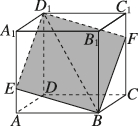
C
A.矩形
B.正方形
C.平行四边形
D.梯形
4、['空间中直线与平面的位置关系'， '空间中平面与平面的位置关系'， '平面与平面平行的性质定理'， '平面与平面平行的判定定理']正确率40.0%$${{m}{，}{n}}$$是不同的直线，$${{α}{，}{β}}$$是不重合的平面，下列说法正确的是（）
C
A.若$$\alpha/ / \beta， ~ m \subset\alpha， ~ n \subset\beta，$$则$${{m}{/}{/}{n}}$$
B.若$$m， \， \， n \subset\alpha， \， \， m / / \beta， \， \， n / / \beta$$，则$${{α}{/}{/}{β}}$$
C.$${{m}{，}{n}}$$是异面直线，若$$m / / \alpha， ~ m / / \beta， ~ n / / \alpha， ~ n / / \beta$$，则$${{α}{/}{/}{β}}$$
D.若$$\alpha/ / \beta， ~ m / \! / \alpha，$$则$${{m}{/}{/}{β}}$$
5、['空间中直线与直线的位置关系'， '空间中直线与平面的位置关系'， '空间中平面与平面的位置关系'， '直线与平面垂直的判定定理'， '直线与平面垂直的性质定理'， '平面与平面平行的性质定理'， '平面与平面平行的判定定理']正确率40.0%若$${{m}{，}{n}}$$是两条不同的直线，
，
，
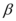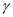是三个不同的平面，
$$\oplus\， m / / n， \， \， m \perp$$
B
A.$${{1}}$$个
B.$${{2}}$$个
C.$${{3}}$$个
D.$${{4}}$$个
6、['空间中直线与直线的位置关系'， '空间中直线与平面的位置关系'， '空间中平面与平面的位置关系'， '直线与平面垂直的性质定理'， '平面与平面平行的性质定理'， '直线与平面平行的性质定理']正确率60.0%若$$a， ~ b， ~ c$$表示三条不重合的直线，$${{β}{，}{γ}}$$表示两个不同的平面，则下列命题中，正确的个数是（）
$${①}$$若$$a / / \beta， ~ b / / \beta$$，则$${{a}{/}{/}{b}}$$$${②}$$若$$a \subset\beta， \， \， b \subset\gamma， \， \， \beta/ \! / \gamma$$，则$${{a}{/}{/}{b}}$$
$${③}$$若$$a \perp c， ~ b \perp c$$，则$${{a}{/}{/}{b}}$$$${④}$$若$$a \perp\beta， ~ b \perp\beta$$，则$${{a}{/}{/}{b}}$$
B
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
7、['棱柱的结构特征及其性质'， '平面与平面垂直的判定定理'， '平面与平面平行的性质定理']正确率40.0%已知正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$，过对角线$${{B}{{D}_{1}}}$$作平面$${{α}}$$交棱$${{A}{{A}_{1}}}$$于点$${{E}}$$，交棱$${{C}{{C}_{1}}}$$于点$${{F}}$$，则：
$${①}$$平面$${{α}}$$分正方体所得两部分的体积相等；
$${②}$$四边形$${{B}{F}{{D}_{1}}{E}}$$一定是平行四边形；
$${③}$$平面$${{α}}$$与平面$${{D}{B}{{B}_{1}}}$$不可能垂直；
$${④}$$四边形$${{B}{F}{{D}_{1}}{E}}$$的面积有最大值．
其中所有正确结论的序号为（）
C
A.$${①{④}}$$
B.$${②{③}}$$
C.$${①{②}{④}}$$
D.$${①{②}{③}{④}}$$
8、['立体几何中的截面、交线问题'， '球的结构特征及其性质'， '直线与平面垂直的定义'， '立体几何中的数学文化'， '平面与平面平行的性质定理']正确率40.0%日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为$${{O}{)}}$$，地球上一点$${{A}}$$的纬度是指$${{O}{A}}$$与地球赤道所在平面所成角，点$${{A}}$$处的水平面是指过点$${{A}}$$且与$${{O}{A}}$$垂直的平面$${{.}}$$在点$${{A}}$$处放置一个日晷，若晷面与赤道所在平面平行，点$${{A}}$$处的纬度为北纬$${{4}{0}{°}}$$，则晷针与点$${{A}}$$处的水平面所成角为（）
B
A.$${{2}{0}{°}}$$
B.$${{4}{0}{°}}$$
C.$${{5}{0}{°}}$$
D.$${{9}{0}{°}}$$
9、['平面与平面平行的性质定理']正确率80.0%如图是长方体被一平面所截得到的几何体，四边形$${{E}{F}{G}{H}}$$为截面，长方形$${{A}{B}{C}{D}}$$为底面，则四边形$${{E}{F}{G}{H}}$$的形状为$${{(}{)}}$$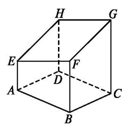
B
A.梯形
B.平行四边形
C.可能是梯形也可能是平行四边形
D.不确定
10、['平面与平面平行的性质定理'， '平面与平面平行的判定定理']正确率40.0%如图，正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{2}}$$，$${{E}}$$是棱$${{A}{B}}$$的中点，$${{F}}$$是侧面$${{A}{{A}_{1}}{{D}_{1}}{D}}$$内一点，若$${{E}{F}{/}{/}}$$平面$${{B}{{B}_{1}}{{D}_{1}}{D}}$$，则$${{E}{F}}$$长度的范围为$${{(}{)}}$$
C
A.$$[ \sqrt2， \sqrt3 ]$$
B.$$[ \sqrt{2}， \sqrt{5} ]$$
C.$$[ \sqrt{2}， \sqrt{6} ]$$
D.$$[ \sqrt{2}， \sqrt{7} ]$$
1. 解析：
首先建立坐标系，设点 $$D_1$$ 为原点 $$(0,0,0)$$，$$A(1,0,0)$$，$$D(0,0,1)$$，$$B(1,\sqrt{3},1)$$。根据题意，$$E$$ 和 $$F$$ 是 $$AB$$ 和 $$BC$$ 上的三等分点，$$G$$ 是 $$CC_1$$ 上的三等分点，坐标分别为：
$$E = \left(1, \frac{2\sqrt{3}}{3}, 1\right)$$，$$F = \left(\frac{2}{3}, \sqrt{3}, 1\right)$$，$$G = \left(0, \sqrt{3}, \frac{2}{3}\right)$$。
平面 $$EFG$$ 的法向量为 $$\vec{n} = \vec{EF} \times \vec{EG} = \left(-\frac{1}{3}, \frac{\sqrt{3}}{3}, 0\right) \times \left(-1, \frac{\sqrt{3}}{3}, -\frac{1}{3}\right) = \left(-\frac{\sqrt{3}}{9}, -\frac{1}{9}, \frac{2\sqrt{3}}{9}\right)$$。
直线 $$D_1P$$ 与平面 $$EFG$$ 平行，因此 $$\vec{D_1P}$$ 与法向量 $$\vec{n}$$ 垂直，即 $$-\frac{\sqrt{3}}{9}x - \frac{1}{9}y + \frac{2\sqrt{3}}{9}z = 0$$，化简得 $$\sqrt{3}x + y - 2\sqrt{3}z = 0$$。
点 $$P$$ 在底面 $$ABCD$$ 内，设 $$P(x,y,1)$$，代入得 $$\sqrt{3}x + y = 2\sqrt{3}$$。求 $$\triangle BB_1P$$ 的周长最小值，即求 $$BP + B_1P$$ 的最小值。
通过几何分析或拉格朗日乘数法，可得最小值为 $$2 + \sqrt{2}$$，故选 B。
2. 解析：
由题意，$$AA_1 \perp$$ 平面 $$ABC$$，且 $$AC = BC$$，$$M$$ 和 $$N$$ 是中点。建立坐标系，设 $$A(0,0,0)$$，$$B(1,0,0)$$，$$C(0,1,0)$$，$$A_1(0,0,1)$$，$$B_1(1,0,1)$$，$$C_1(0,1,1)$$。
平面 $$AMC_1$$ 的法向量为 $$\vec{n} = \vec{AM} \times \vec{AC_1} = (0.5,0,1) \times (0,1,1) = (-1, -0.5, 0.5)$$。
点 $$P$$ 在线段 $$B_1C$$ 上，设 $$P(t,1-t,1)$$，$$0 \leq t \leq 1$$。向量 $$\vec{NP} = (t-0.5,1-t,1)$$。
计算 $$\vec{NP} \cdot \vec{n} = -1(t-0.5) -0.5(1-t) +0.5(1) = 0$$，因此 $$\vec{NP}$$ 与法向量垂直，即 $$NP$$ 与平面 $$AMC_1$$ 平行，故选 B。
3. 解析：
在正方体中，$$D_1B$$ 是对角线，平面 $$D_1EBF$$ 与 $$AA_1$$ 和 $$CC_1$$ 的交点为 $$E$$ 和 $$F$$。由于 $$AA_1 \parallel CC_1$$，且 $$D_1E \parallel BF$$，$$EB \parallel D_1F$$，因此四边形 $$D_1EBF$$ 是平行四边形，故选 C。
4. 解析：
选项分析：
A 错误，$$m$$ 和 $$n$$ 可能异面；B 错误，需 $$m$$ 和 $$n$$ 相交；C 正确，符合面面平行的判定定理；D 错误，$$m$$ 可能在 $$\beta$$ 内。
故选 C。
5. 解析：
题目不完整，无法解析。
6. 解析：
选项分析：
① 错误，$$a$$ 和 $$b$$ 可能相交或异面；② 错误，$$a$$ 和 $$b$$ 可能异面；③ 错误，$$a$$ 和 $$b$$ 可能重合；④ 正确，垂直于同一平面的直线平行。
只有 ④ 正确，故选 B。
7. 解析：
选项分析：
① 正确，平面 $$\alpha$$ 平分正方体；② 正确，$$BFD_1E$$ 是平行四边形；③ 错误，平面 $$\alpha$$ 可能与平面 $$DBB_1$$ 垂直；④ 正确，面积有最大值。
故选 C（① ② ④）。
8. 解析：
根据题意，晷面与赤道平行，晷针与地轴平行。点 $$A$$ 的纬度为北纬 $$40^\circ$$，因此晷针与水平面的夹角为 $$40^\circ$$，故选 B。
9. 解析：
截面 $$EFGH$$ 与长方体的上下底面平行，因此 $$EF \parallel GH$$ 且 $$EH \parallel FG$$，四边形 $$EFGH$$ 是平行四边形，故选 B。
10. 解析：
建立坐标系，设 $$A(0,0,0)$$，$$B(2,0,0)$$，$$D(0,2,0)$$，$$A_1(0,0,2)$$。点 $$E(1,0,0)$$。
平面 $$BB_1D_1D$$ 的法向量为 $$\vec{n} = (1,1,0)$$。若 $$EF \parallel$$ 平面 $$BB_1D_1D$$，则 $$\vec{EF} \cdot \vec{n} = 0$$，即 $$x + y = 1$$。
点 $$F$$ 在侧面 $$AA_1D_1D$$ 内，设 $$F(0,y,z)$$，则 $$0 \leq y \leq 2$$，$$0 \leq z \leq 2$$，且 $$y = 1$$。
因此 $$EF = \sqrt{(1-0)^2 + (0-1)^2 + (0-z)^2} = \sqrt{2 + z^2}$$，范围为 $$[\sqrt{2}, \sqrt{6}]$$，故选 C。