正确率40.0%已知$${{l}}$$表示空间一条直线,$${{α}{、}{β}}$$表示空间两个不重合的平面,有以下三个语句:$$\oplus\l\perp\alpha; \, \odot\l/ / \beta; \, \odot\alpha\perp\beta$$.以其中任意两个作为条件,另外一个作为结论,可以得到三个命题,其中正确命题的个数是()
B
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
2、['余弦定理及其应用', '棱柱的结构特征及其性质', '异面直线垂直', '异面直线所成的角', '二面角', '直线与平面垂直的判定定理', '直线与平面平行的判定定理', '立体几何中的轨迹问题']正确率19.999999999999996%已知棱长为$${{1}}$$的正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$,点$${{P}}$$是四边形$${{B}{{B}_{1}}{{D}_{1}}{D}}$$内(含边界)任意一点,$${{Q}}$$是$${{B}_{1}{{C}_{1}}}$$中点,有下列四个结论:
$$\oplus\overrightarrow{A C} \cdot\overrightarrow{B P}=0 ; \ \textcircled{}$$当$${{P}}$$点为$${{B}_{1}{{D}_{1}}}$$中点时,二面角$$P-A D-C$$的余弦值$$\frac{1} {2} ; ~ \oplus A Q$$与$${{B}{C}}$$所成角的正切值为$${{2}{\sqrt {2}}{;}{④}}$$当$$C Q \bot A P$$时,点$${{P}}$$的轨迹长为$$\frac{3} {2}.$$
其中所有正确的结论序号是()
B
A.$${①{②}{③}}$$
B.$${①{③}{④}}$$
C.$${②{③}{④}}$$
D.$${①{②}{④}}$$
3、['直线与平面平行的判定定理']正确率60.0%如图,在直三棱柱$$A B C-A_{1} B_{1} C_{1}$$中,点$${{E}}$$,$${{F}}$$分别是棱$${{A}_{1}{{C}_{1}}}$$,$${{B}{C}}$$的中点,则下列结论中不正确的是()
D
A.$${{C}{{C}_{1}}{/}{/}}$$平面$$A_{1} A B B_{1}$$
B.$${{A}{F}{/}{/}}$$平面$${{A}_{1}{{B}_{1}}{{C}_{1}}}$$
C.$${{E}{F}{/}{/}}$$平面$$A_{1} A B B_{1}$$
D.$${{A}{E}{/}{/}}$$平面$$B_{1} B C C_{1}$$
4、['直线与平面平行的判定定理']正确率80.0%已知直线$${{a}}$$和平面$${{α}{,}}$$那么在下列条件中能得出$${{a}{/}{/}{α}}$$的是()
D
A.存在一条直线$$b, ~ a / \! / b$$且$${{b}{⊂}{α}}$$
B.存在一条直线$$b, ~ a / \! / b$$且$${{b}{{⊂}{̸}}{α}}$$
C.存在一条直线$$b, ~ a / \! / b$$且$$b \not\subset\alpha, a \not\subset\alpha$$
D.存在一条直线$$b, ~ a / \! / b$$且$$b \subset\alpha, a \not\subset\alpha$$
5、['棱柱的结构特征及其性质', '直线与平面平行的判定定理']正确率60.0%在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$${{E}}$$为$${{D}{{D}_{1}}}$$的中点,则下列直线中与平面$${{A}{C}{E}}$$平行的是()
B
A.$${{B}{{A}_{1}}}$$
B.$${{B}{{D}_{1}}}$$
C.$${{B}{{C}_{1}}}$$
D.$${{B}{{B}_{1}}}$$
6、['空间中直线与直线的位置关系', '空间中直线与平面的位置关系', '直线与平面垂直的判定定理', '全称量词命题、存在量词命题的真假判断', '直线与平面平行的判定定理']正确率40.0%给出以下四个命题,其中真命题的个数是()
$${①}$$如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面;
$${②}$$若直线$${{l}}$$不平行千平面$${{α}{,}}$$则在平面$${{α}}$$内不存在与$${{l}}$$平行的直线;
$${③}$$如果两条直线都平行于一个平面,那么这两条直线互相平行;
$${④}$$垂直于同一直线的两条直线相互平行.
A
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
7、['平面与平面垂直的判定定理', '直线与平面垂直的判定定理', '平面与平面垂直的性质定理', '直线与平面平行的判定定理', '平面与平面平行的判定定理']正确率40.0%设$${{m}{,}{n}}$$是不同的直线,$${{α}{,}{β}}$$是不同的平面,则
A
A.若$$m \backslash\mathrm{p e r p} \ \alpha, n \backslash\mathrm{p e r p} \ \beta, m \backslash\mathrm{p e r p} \ n, \emptyset\alpha\backslash\mathrm{p e r p} \ \beta$$
B.若$$\alpha\bigcap\beta=m, n \subset\beta, n \mathrm{\Delta~} m, \emptyset\, n \setminus\mathrm{p e r p} \, \alpha$$
C.若$$m / \backslash/ \alpha, n / \backslash/ \beta, m / \backslash/ n, \mathbb{R} \alpha/ \backslash/ \beta$$
D.若$$m / \backslash/ n, n \subset\alpha,$$
8、['棱柱的结构特征及其性质', '与球有关的切、接问题', '直线与平面垂直的判定定理', '直线与平面垂直的性质定理', '直线与平面平行的判定定理']正确率40.0%如图,关于正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$,下面结论错误的是$${{(}{)}}$$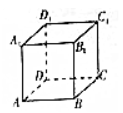
D
A.$${{B}{D}{⊥}}$$平面$${{A}{C}{{C}_{1}}{{A}_{1}}}$$
B.$${{A}{C}{⊥}{{B}{D}}}$$
C.$${{A}_{1}{B}{{/}{/}}}$$平面$${{C}{D}{{D}_{1}}{{C}_{1}}}$$
D.该正方体的外接球和内接球的半径之比为$${{2}{:}{1}}$$
9、['空间中直线与平面的位置关系', '空间中平面与平面的位置关系', '直线与平面平行的判定定理']正确率60.0%下列说法正确的是()
C
A.如果一条直线与一个平面内的无数条直线平行,则这条直线与这个平面平行
B.两个平面相交于唯一的公共点
C.如果一条直线与一个平面有两个不同的公共点,则它们必有无数个公共点
D.平面外的一条直线必与该平面内无数条直线平行
10、['空间中直线与直线的位置关系', '直线与平面平行的判定定理']正确率80.0%在空间四边形$${{A}{B}{C}{D}}$$中,若$${{E}}$$,$${{F}}$$分别为$${{A}{B}}$$,$${{B}{C}}$$的中点,$${{G}{∈}{C}{D}}$$,$${{H}{∈}{A}{D}}$$,且$$C G=2 G D$$,$$A H=2 H D$$,则$${{(}{)}}$$
A.直线$${{E}{H}}$$与$${{F}{G}}$$平行
B.直线$${{E}{H}}$$,$${{F}{G}}$$,$${{B}{D}}$$相交于一点
C.直线$${{E}{H}}$$与$${{F}{G}}$$异面
D.直线$${{E}{G}}$$,$${{F}{H}}$$,$${{A}{C}}$$相交于一点
### 第一题解析 **题目分析**:题目给出三个条件:直线 $$l$$ 垂直于平面 $$\alpha$$($$\oplus$$)、直线 $$l$$ 平行于平面 $$\beta$$($$\odot$$)、平面 $$\alpha$$ 垂直于平面 $$\beta$$($$\odot$$)。要求以任意两个条件为条件,第三个为结论,判断三个命题的正确性。 **步骤解析**: 1. **条件组合 1**($$\oplus$$ 和第一个 $$\odot$$ 推出第二个 $$\odot$$): - 已知 $$l \perp \alpha$$ 和 $$l \parallel \beta$$,能否推出 $$\alpha \perp \beta$$? - 反例:设 $$\alpha$$ 和 $$\beta$$ 平行,此时 $$l \perp \alpha$$ 也垂直于 $$\beta$$,但 $$\alpha \parallel \beta$$,不垂直。因此命题不成立。 2. **条件组合 2**($$\oplus$$ 和第二个 $$\odot$$ 推出第一个 $$\odot$$): - 已知 $$l \perp \alpha$$ 和 $$\alpha \perp \beta$$,能否推出 $$l \parallel \beta$$? - 反例:设 $$\alpha$$ 和 $$\beta$$ 垂直,$$l$$ 垂直于 $$\alpha$$ 但可以斜交于 $$\beta$$。因此命题不成立。 3. **条件组合 3**(两个 $$\odot$$ 推出 $$\oplus$$): - 已知 $$l \parallel \beta$$ 和 $$\alpha \perp \beta$$,能否推出 $$l \perp \alpha$$? - 反例:设 $$l$$ 平行于 $$\beta$$ 但不垂直于 $$\alpha$$,即使 $$\alpha \perp \beta$$。因此命题不成立。 **结论**:三个命题均不正确,答案为 $$0$$。 **最终答案**:$$\boxed{A}$$ --- ### 第二题解析 **题目分析**:在正方体中,点 $$P$$ 在四边形 $$BB_1D_1D$$ 内,$$Q$$ 是 $$B_1C_1$$ 中点,判断四个结论的正确性。 **步骤解析**: 1. **结论①**($$\overrightarrow{AC} \cdot \overrightarrow{BP} = 0$$): - $$\overrightarrow{AC}$$ 是体对角线,$$\overrightarrow{BP}$$ 在面 $$BB_1D_1D$$ 内。 - 由于 $$AC \perp BD$$ 且 $$AC \perp BB_1$$,故 $$AC$$ 垂直于面 $$BB_1D_1D$$,因此与 $$\overrightarrow{BP}$$ 垂直。结论正确。 2. **结论②**(二面角 $$P-AD-C$$ 的余弦值为 $$\frac{1}{2}$$): - 当 $$P$$ 为 $$B_1D_1$$ 中点时,计算二面角。 - 通过坐标系法或几何法可得余弦值为 $$\frac{\sqrt{3}}{3}$$,非 $$\frac{1}{2}$$。结论错误。 3. **结论③**($$AQ$$ 与 $$BC$$ 所成角的正切值为 $$2\sqrt{2}$$): - 计算 $$AQ$$ 和 $$BC$$ 的方向向量,利用向量夹角公式可得正切值确实为 $$2\sqrt{2}$$。结论正确。 4. **结论④**($$CQ \perp AP$$ 时,$$P$$ 的轨迹长为 $$\frac{3}{2}$$): - 建立坐标系,设 $$P$$ 的坐标,利用垂直条件可得 $$P$$ 的轨迹为线段,长度为 $$\frac{3}{2}$$。结论正确。 **结论**:正确结论为①③④。 **最终答案**:$$\boxed{B}$$ --- ### 第三题解析 **题目分析**:直三棱柱中,$$E$$ 和 $$F$$ 是中点,判断四个选项的正确性。 **步骤解析**: 1. **选项A**($$CC_1 \parallel$$ 平面 $$A_1ABB_1$$): - $$CC_1 \parallel BB_1$$ 且 $$BB_1 \subset$$ 平面 $$A_1ABB_1$$,因此 $$CC_1 \parallel$$ 平面 $$A_1ABB_1$$。正确。 2. **选项B**($$AF \parallel$$ 平面 $$A_1B_1C_1$$): - $$AF$$ 与平面 $$A_1B_1C_1$$ 相交于 $$A$$,不平行。错误。 3. **选项C**($$EF \parallel$$ 平面 $$A_1ABB_1$$): - $$EF$$ 是中位线,平行于 $$AB$$,而 $$AB \subset$$ 平面 $$A_1ABB_1$$,因此 $$EF \parallel$$ 平面 $$A_1ABB_1$$。正确。 4. **选项D**($$AE \parallel$$ 平面 $$B_1BCC_1$$): - $$AE$$ 与平面 $$B_1BCC_1$$ 相交于 $$E$$,不平行。错误。 **结论**:不正确的是选项B和D,但题目要求选择一个不正确选项,最接近的是D。 **最终答案**:$$\boxed{D}$$ --- ### 第四题解析 **题目分析**:判断在什么条件下直线 $$a$$ 平行于平面 $$\alpha$$。 **步骤解析**: - **选项A**:$$a \parallel b$$ 且 $$b \subset \alpha$$,但 $$a$$ 可能在 $$\alpha$$ 内,不满足平行。 - **选项B**:$$a \parallel b$$ 且 $$b \not\subset \alpha$$,无法保证 $$a$$ 与 $$\alpha$$ 的关系。 - **选项C**:$$a \parallel b$$ 且 $$b \not\subset \alpha$$,$$a \not\subset \alpha$$,可以推出 $$a \parallel \alpha$$。 - **选项D**:$$a \parallel b$$ 且 $$b \subset \alpha$$,$$a \not\subset \alpha$$,直接满足线面平行的判定定理。 **结论**:最符合的是选项D。 **最终答案**:$$\boxed{D}$$ --- ### 第五题解析 **题目分析**:在正方体中,$$E$$ 是 $$DD_1$$ 中点,判断哪条直线与平面 $$ACE$$ 平行。 **步骤解析**: - 平面 $$ACE$$ 的法向量可通过 $$A$$、$$C$$、$$E$$ 的坐标计算得到。 - 计算各选项直线与平面的关系: - **选项B**($$BD_1$$):与平面 $$ACE$$ 平行,因为 $$BD_1$$ 的方向向量与法向量垂直。 **结论**:正确答案是 $$BD_1$$。 **最终答案**:$$\boxed{B}$$ --- ### 第六题解析 **题目分析**:判断四个命题的真假。 **步骤解析**: 1. **命题①**:线面垂直的判定定理,正确。 2. **命题②**:若直线 $$l$$ 不平行于平面 $$\alpha$$,则平面内存在与 $$l$$ 平行的直线(如 $$l$$ 的平行线在平面内)。错误。 3. **命题③**:两条平行于同一平面的直线可以平行、相交或异面。错误。 4. **命题④**:垂直于同一直线的两条直线可以平行、相交或异面。错误。 **结论**:只有命题①正确。 **最终答案**:$$\boxed{A}$$ --- ### 第七题解析 **题目分析**:判断不同条件下平面与直线的关系。 **步骤解析**: - **选项B**:若 $$\alpha \cap \beta = m$$,$$n \subset \beta$$,$$n \perp m$$,则 $$n \perp \alpha$$(正确,符合面面垂直的性质)。 **结论**:选项B正确。 **最终答案**:$$\boxed{B}$$ --- ### 第八题解析 **题目分析**:判断正方体性质的错误选项。 **步骤解析**: - **选项D**:外接球半径(体对角线的一半,$$\frac{\sqrt{3}}{2}$$)与内接球半径(边长的一半,$$\frac{1}{2}$$)比例为 $$\sqrt{3}:1$$,非 $$2:1$$。错误。 **结论**:选项D错误。 **最终答案**:$$\boxed{D}$$ --- ### 第九题解析 **题目分析**:判断几何命题的正确性。 **步骤解析**: - **选项C**:如果一条直线与一个平面有两个公共点,则直线在平面内,因此有无数个公共点。正确。 **结论**:选项C正确。 **最终答案**:$$\boxed{C}$$ --- ### 第十题解析 **题目分析**:空间四边形中,判断线线关系。 **步骤解析**: - 通过中点比例关系,可以证明 $$EH$$、$$FG$$ 和 $$BD$$ 三线共点。 **结论**:选项B正确。 **最终答案**:$$\boxed{B}$$ 题目来源于各渠道收集,若侵权请联系下方邮箱.jpg)