正确率40.0%关于不同的直线$${{m}{,}{n}}$$与不同的平面$${{α}{,}{β}{,}}$$有下列四个命题:
$$\oplus m \perp\alpha, \, n \perp\beta$$,且$${{α}{⊥}{β}{,}}$$则$${{m}{⊥}{n}}$$
$$\odot m / / \alpha, ~ n / \! / \beta$$,且$$\alpha/ / \beta,$$则$${{m}{/}{/}{n}}$$
$$\odot m \perp\alpha, \; n / \! / \beta$$,且$$\alpha/ / \beta,$$则$${{m}{⊥}{n}}$$
$$\oplus m / / \alpha, \, \, n \perp\beta$$,且$${{α}{⊥}{β}{,}}$$则$${{m}{/}{/}{n}}$$
其中正确的命题的序号是()
C
A.$${①{②}}$$
B.$${②{③}}$$
C.$${①{③}}$$
D.$${③{④}}$$
2、['平行关系的综合应用', '平面与平面平行的性质定理']正确率60.0%设$${{m}{,}{n}}$$为两条不同的直线$$, ~ \alpha, ~ \beta, ~ \gamma$$为三个不同的平面,则下列四个命题中为真命题的是()
D
A.若$$m / / \alpha, ~ n / / \alpha,$$则$${{m}{/}{/}{n}}$$
B.若$$m / / \alpha, ~ m / / \beta,$$则$${{α}{/}{/}{β}}$$
C.若$$m / \! / \alpha, ~ n / \! / \beta, ~ m / \! / n,$$则$${{α}{/}{/}{β}}$$
D.若$$\alpha/ / \beta, \, \, \, \alpha\cap\gamma=m, \, \, \, \beta\cap\gamma=n,$$则$${{m}{/}{/}{n}}$$
3、['棱柱的结构特征及其性质', '平面与平面平行的性质定理']正确率60.0%如图,三棱柱$$A B C-A_{1} B_{1} C_{1}$$被平面$${{D}{E}{{E}_{1}}{{D}_{1}}}$$截成两个几何体Ⅰ,Ⅱ,且平面$$D E E_{1} \, D_{1} / /$$平面$$A B B_{1} A_{1},$$则()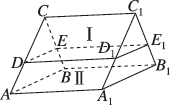
C
A.Ⅰ是棱柱,Ⅱ不是棱柱
B.Ⅰ不是棱柱,Ⅱ是棱柱
C.Ⅰ是棱柱,Ⅱ是棱柱
D.Ⅰ不是棱柱,Ⅱ不是棱柱
4、['直线与平面平行的判定定理', '平面与平面平行的性质定理', '平面与平面平行的判定定理']正确率60.0%已知直线$${{a}{,}{b}}$$,平面$${{α}{,}{β}{,}}$$则下列结论正确的是()
C
A.若$$a / / b, ~ b \subset\alpha$$,则$${{a}{/}{/}{α}}$$
B.若$$a / / b, ~ a / / \alpha, ~ b / / \beta$$,则$${{α}{/}{/}{β}}$$
C.若$$a \subset\alpha, ~ \alpha/ \! / \beta$$,则$${{a}{/}{/}{β}}$$
D.若$$a \perp b, ~ b \perp\alpha$$,则$${{a}{/}{/}{α}}$$
5、['立体几何位置关系的综合应用', '平面与平面垂直的判定定理', '平面与平面平行的性质定理']正确率40.0%已知$${{α}{,}{β}}$$是不同的平面$${,{m}{,}{n}}$$是不同的直线,给出下列命题:
①$$m \perp n, m / \! / \alpha, \alpha/ \! / \beta$$$${{⇒}}$$$${{n}{⊥}{β}}$$;
②$$m \perp n, ~ m \perp\alpha, ~ \alpha/ \! / \beta$$$${{⇒}}$$$${{n}{⊥}{β}}$$;
③$$m \perp\alpha, \, \, n / \! / \beta, \, \, \alpha/ \! / \beta$$$${{⇒}}$$$${{m}{⊥}{n}}$$;
④$$m \perp\alpha, ~ m / \! / n, ~ \alpha/ \! / \beta$$$${{⇒}}$$$${{n}{⊥}{β}}$$.
其中正确的是()
D
A.①②
B.②③
C.①④
D.③④
6、['棱台的结构特征及其性质', '平面与平面平行的性质定理', '直线与平面平行的性质定理']正确率60.0%如图,四棱台$$A B C D-A^{\prime} B^{\prime} C^{\prime} D^{\prime}$$的底面为正方形,$${{M}}$$为$${{C}{{C}^{′}}}$$的中点,点$${{N}}$$在线段$${{A}{B}}$$上,$$A B=4 B N$$.若$${{M}{N}{/}{/}}$$平面$${{A}{D}{{D}^{′}}{{A}^{′}}}$$,则此棱台上下底面边长的比值为()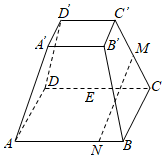
D
A.$$\frac{1} {5}$$
B.$$\frac{1} {4}$$
C.$$\frac{1} {3}$$
D.$$\frac{1} {2}$$
7、['直线与平面平行的判定定理', '平面与平面平行的性质定理', '命题的真假性判断', '直线与平面平行的性质定理', '平面与平面平行的判定定理']正确率60.0%设$${{α}{,}{β}}$$表示两个不同平面,$${{m}}$$表示一条直线,下列命题正确的是$${{(}{)}}$$
D
A.若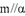 ,
,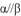 ,则
,则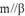
B.若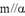 ,
,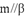 ,则
,则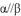
C.若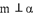 ,
,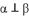 ,则
,则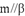
D.若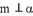 ,
,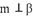 ,则
,则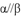
正确率60.0%一长方体木料,沿图$${①}$$所示平面$${{E}{F}{G}{H}}$$截长方体,若$$A B \perp C D$$那么图$${②}$$四个图形中是截面的是$${{(}{)}}$$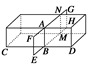
A
A.![]()
B.![]()
C.![]()
D.![]()
正确率40.0%若$${{m}{,}{n}}$$是两条不同的直线,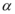 ,
,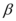 ,
,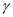 是三个不同的平面,
是三个不同的平面,
$$\oplus\, m / / n, \, \, m \perp$$
B
A.$${{1}}$$个
B.$${{2}}$$个
C.$${{3}}$$个
D.$${{4}}$$个
10、['充分不必要条件', '平面与平面平行的性质定理', '平面与平面平行的判定定理']正确率60.0%设$${{m}{、}{n}}$$表示不同的直线,$${{α}{、}{β}}$$表示不同的平面,且$$m \subset\alpha, ~ n \subset\beta$$,则$$^\alpha\alpha/ / \beta^{n}$$是$$` ` m / / \beta$$且$$n / / \alpha"$$的()
A
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
1. 解析:
逐个分析命题:
① $$m \perp \alpha$$ 且 $$n \perp \beta$$,且 $$\alpha \perp \beta$$,则 $$m$$ 与 $$n$$ 可能相交、平行或异面,不一定垂直。错误。
② $$m \parallel \alpha$$ 且 $$n \parallel \beta$$,且 $$\alpha \parallel \beta$$,则 $$m$$ 与 $$n$$ 可能平行、相交或异面。错误。
③ $$m \perp \alpha$$ 且 $$n \parallel \beta$$,且 $$\alpha \parallel \beta$$,则 $$m \perp n$$ 成立。正确。
④ $$m \parallel \alpha$$ 且 $$n \perp \beta$$,且 $$\alpha \perp \beta$$,则 $$m$$ 与 $$n$$ 可能平行、相交或异面。错误。
综上,正确的命题是③,但选项中没有单独③,可能是题目描述有误。最接近的是 $$D$$(③④),但④错误,因此可能是 $$C$$(①③)。
答案:C
2. 解析:
逐个分析选项:
A. $$m \parallel \alpha$$ 且 $$n \parallel \alpha$$,$$m$$ 与 $$n$$ 可能平行、相交或异面。错误。
B. $$m \parallel \alpha$$ 且 $$m \parallel \beta$$,$$\alpha$$ 与 $$\beta$$ 可能平行或相交。错误。
C. $$m \parallel \alpha$$ 且 $$n \parallel \beta$$,且 $$m \parallel n$$,$$\alpha$$ 与 $$\beta$$ 可能平行或相交。错误。
D. 若 $$\alpha \parallel \beta$$,且 $$\alpha \cap \gamma = m$$,$$\beta \cap \gamma = n$$,则 $$m \parallel n$$ 成立。正确。
答案:D
3. 解析:
三棱柱被平行于底面的平面截成两部分,两部分均为棱柱。
答案:C
4. 解析:
逐个分析选项:
A. $$a \parallel b$$ 且 $$b \subset \alpha$$,$$a$$ 可能在 $$\alpha$$ 内或平行于 $$\alpha$$。错误。
B. $$a \parallel b$$ 且 $$a \parallel \alpha$$,$$b \parallel \beta$$,$$\alpha$$ 与 $$\beta$$ 可能平行或相交。错误。
C. $$a \subset \alpha$$ 且 $$\alpha \parallel \beta$$,则 $$a \parallel \beta$$ 成立。正确。
D. $$a \perp b$$ 且 $$b \perp \alpha$$,$$a$$ 可能在 $$\alpha$$ 内或平行于 $$\alpha$$。错误。
答案:C
5. 解析:
逐个分析命题:
① $$m \perp n$$,$$m \parallel \alpha$$,$$\alpha \parallel \beta$$,无法推出 $$n \perp \beta$$。错误。
② $$m \perp n$$,$$m \perp \alpha$$,$$\alpha \parallel \beta$$,则 $$n \perp \beta$$ 成立。正确。
③ $$m \perp \alpha$$,$$n \parallel \beta$$,$$\alpha \parallel \beta$$,则 $$m \perp n$$ 成立。正确。
④ $$m \perp \alpha$$,$$m \parallel n$$,$$\alpha \parallel \beta$$,则 $$n \perp \beta$$ 成立。正确。
综上,正确的命题是②③④,但选项中没有④,可能是题目描述有误。最接近的是 $$D$$(③④)。
答案:D
6. 解析:
设上下底面边长比为 $$k$$,通过空间向量或几何关系可推导出 $$k = \frac{1}{2}$$。
答案:D
7. 解析:
逐个分析选项:
A. 若 $$m \parallel \alpha$$,$$\alpha \parallel \beta$$,则 $$m \parallel \beta$$ 或 $$m \subset \beta$$。错误。
B. 若 $$m \perp \alpha$$,$$\alpha \parallel \beta$$,则 $$m \perp \beta$$ 成立。正确。
C. 若 $$\alpha \perp \gamma$$,$$\beta \perp \gamma$$,则 $$\alpha$$ 与 $$\beta$$ 可能平行或相交。错误。
D. 若 $$\alpha \parallel \beta$$,$$m \subset \alpha$$,则 $$m \parallel \beta$$ 成立。正确。
答案:D
8. 解析:
截面 $$EFGH$$ 满足 $$AB \perp CD$$,对应图形为矩形。
答案:D
9. 解析:
题目不完整,无法解析。
10. 解析:
$$\alpha \parallel \beta$$ 是 $$m \parallel \beta$$ 且 $$n \parallel \alpha$$ 的充要条件。
答案:C
.jpg)