.jpg)
正确率60.0%已知$${{m}{，}{n}}$$是两条不同的直线$${，{α}{，}{β}}$$是两个不同的平面$${，{m}}$$$${{⊂}{α}}$$，$${{n}{⊂}{β}}$$，下列结论中正确的是（）
D
A.若$$m / / n，$$则$${{α}{/}{/}{β}}$$
B.若$$\alpha/ / \beta，$$则$${{m}{/}{/}{n}}$$
C.若$${{m}}$$与$${{n}}$$不相交，则$${{α}{/}{/}{β}}$$
D.若$$\alpha/ / \beta，$$则$${{m}}$$与$${{n}}$$不相交
2、['平行关系的综合应用']正确率60.0%下列说法正确的是（）
D
A.一条直线与一个平面平行，它就和这个平面内的任意一条直线平行
B.平行于同一个平面的两条直线平行
C.与两个相交平面的交线平行的直线，必平行于这两个平面
D.平面外两条平行直线中的一条与这个平面平行，则另一条也与这个平面平行
3、['平行关系的综合应用']正确率60.0%已知$$a， ~ b， ~ c$$为三条不同的直线，$$\alpha， ~ \beta， ~ \gamma$$为三个不同的平面，则下列说法正确的是（）
D
A.若$$a / / b， ~ b \subset\alpha$$，则$${{a}{/}{/}{α}}$$
B.若$$a \subset\alpha， \， \， b \subset\beta， \， \， a / / b$$，则$${{α}{/}{/}{β}}$$
C.若$$\alpha/ / \beta， ~ a / / \alpha，$$则$${{a}{/}{/}{β}}$$
D.若$$\alpha\cap\beta=a， \， \， \， \beta\cap\gamma=b， \， \， \， \alpha\cap\gamma=c， \， \， \， a / / b，$$则$${{b}{/}{/}{c}}$$
4、['平行关系的综合应用']正确率60.0%设$${{l}}$$表示直线$${，{α}{，}{β}}$$表示平面，有以下说法：
①若$$l / \! / \alpha，$$则$${{α}}$$内有无数条直线与$${{l}}$$平行；
②若$$l / \! / \alpha，$$则$${{α}}$$内任意一条直线与$${{l}}$$平行；
③若$$\alpha/ / \beta，$$则对于$${{α}}$$内的一条确定的直线$${{a}{，}}$$在$${{β}}$$内仅有唯一的直线与$${{a}}$$平行.
其中正确说法的个数为（）
B
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
5、['垂直关系的综合应用'， '平行关系的综合应用']正确率60.0%已知两个不同的平面$${{α}{，}{β}}$$和两条不重合的直线$${{m}{，}{n}}$$，有下列三个命题：
$${①}$$若$$m / \! / n， ~ m \perp\alpha$$，则$${{n}{⊥}{α}}$$；$${②}$$若$$m \perp\alpha， ~ m \perp\beta$$，则$$\alpha/ / \beta;$$
$${③}$$若$$m \perp\alpha， ~ m / \! / n， ~ n \subset\beta$$，则$${{α}{⊥}{β}}$$其中正确命题的个数是（）
D
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
6、['空间中直线与平面的位置关系'， '平行关系的综合应用'， '平面与平面平行的判定定理']正确率40.0%下列命题中是真命题的个数是（）
$${（{1}{）}}$$垂直于同一条直线的两条直线互相平行
$${（{2}{）}}$$与同一个平面夹角相等的两条直线互相平行
$${（{3}{）}}$$平行于同一个平面的两条直线互相平行
$${（{4}{）}}$$两条直线能确定一个平面
$${（{5}{）}}$$垂直于同一个平面的两个平面平行
A
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
7、['平行关系的综合应用'， '直线与平面平行的判定定理']正确率40.0%能保证直线$${{a}}$$与平面$${{α}}$$平行的条件是（）
D
A.$$b \subset\alpha， ~ a / \! / b$$
B.$$b \subset\alpha， \， \， \， c \subset\alpha， \， \， \， a / \! / b， \， \， \， a / \! / c$$
C.$$b \subset\alpha， \， \， \， A \in a， \， \， \， B \in a， \， \， \， C \in b， \， \， \， D \in b$$，且$$A C=B D$$
D.$$a \not\subset\alpha， \， \， b \subset\alpha， \， \， a / / b$$
8、['垂直关系的综合应用'， '平行关系的综合应用']正确率40.0%设$${{m}{，}{n}}$$是两条不同的直线，$${{α}{，}{β}}$$是两个不同的平面，
$${①}$$若$$m / \! / \alpha， n / \! / \alpha$$，则$${{m}{/}{/}{n}}$$；
$${②}$$若$$\alpha/ / \beta， m \bot\alpha， n / / \beta$$，则$${{m}{⊥}{n}}$$；
$${③}$$若$$m \bot\alpha， n \subset\beta， m \bot n$$，则$${{α}{⊥}{β}}$$；
$${④}$$若$$\alpha\bot\beta， m \bot\beta， m \notin\alpha$$则$${{m}{/}{/}{α}}$$．
以上四种说法中正确的序号是
D
A.$${①{③}}$$
B.$${①{④}}$$
C.$${②{③}}$$
D.$${②{④}}$$
9、['空间中直线与直线的位置关系'， '空间中平面与平面的位置关系'， '垂直关系的综合应用'， '平行关系的综合应用']正确率60.0%已知$${{m}{，}{n}}$$是空间中两条不同的直线，$${{α}{，}{β}}$$是两个不同的平面，有以下结论：
$$\odot m \subset\alpha， n \subset\beta， m \setminus\mathrm{p e r p} n \Rightarrow\alpha\setminus\mathrm{p e r p} \ \beta$$$$\oplus m / / \beta， n / / \beta， m \subset\alpha， n \subset\alpha\Rightarrow\alpha/ / \beta$$
$$\odot m \mathrm{\bf~ \beta，} n \mathrm{\bf~ \ p e r p ~} \alpha\mathrm{，} m \mathrm{\bf~ \ p e r p ~} n \Rightarrow\alpha\mathrm{\bf~ \ p e r p ~} \beta$$$$\oplus\textsubscript{m} \subset\alpha， \! m / / n \Rightarrow\! n / / \alpha$$．
其中正确结论的个数是
B
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
10、['空间中直线与直线的位置关系'， '空间中直线与平面的位置关系'， '空间中平面与平面的位置关系'， '垂直关系的综合应用'， '平行关系的综合应用']正确率60.0%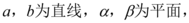
下列正确的是（）
D
A.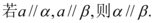
B.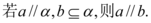
C.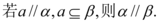
D.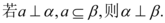
以下是各题的详细解析：
选项分析：
A. 若 $$m \parallel n$$，平面 $$\alpha$$ 和 $$\beta$$ 可能相交（如长方体的上下底面与侧棱）。错误。
B. 若 $$\alpha \parallel \beta$$，直线 $$m$$ 和 $$n$$ 可能平行或异面（如长方体的上下底面内的直线）。错误。
C. 若 $$m$$ 与 $$n$$ 不相交，它们可能平行或异面，平面 $$\alpha$$ 和 $$\beta$$ 可能相交或平行。错误。
D. 若 $$\alpha \parallel \beta$$，直线 $$m$$ 和 $$n$$ 无交点（平行或异面）。正确。
答案：D
选项分析：
A. 直线与平面平行，仅与平面内的某些直线平行（如中位线），非任意。错误。
B. 平行于同一平面的两条直线可能平行、相交或异面（如长方体的侧棱）。错误。
C. 与两相交平面交线平行的直线，可能平行于其中一个平面或在其内。错误。
D. 若一条平行直线与平面平行，另一条也平行（平行传递性）。正确。
答案：D
选项分析：
A. 若 $$a \parallel b$$ 且 $$b \subset \alpha$$，$$a$$ 可能在 $$\alpha$$ 外与之平行。正确。
B. 单凭 $$a \parallel b$$ 无法推出 $$\alpha \parallel \beta$$（平面可能相交）。错误。
C. 若 $$\alpha \parallel \beta$$ 且 $$a \parallel \alpha$$，$$a$$ 可能在 $$\beta$$ 内或与之平行。错误。
D. 由三平面两两交线平行（$$a \parallel b$$）可推出 $$b \parallel c$$（类似三棱柱截面）。正确。
答案：D
说法分析：
① 若 $$l \parallel \alpha$$，$$\alpha$$ 内存在无数条与 $$l$$ 平行的直线。正确。
② 若 $$l \parallel \alpha$$，$$\alpha$$ 内存在与 $$l$$ 异面的直线。错误。
③ 若 $$\alpha \parallel \beta$$，$$\beta$$ 内所有与 $$a$$ 平行的直线均平行（平行平面性质）。错误。
正确说法仅①。
答案：B
命题分析：
① 平行直线中一条垂直平面，另一条也垂直。正确。
② 两条直线均垂直两平面，则平面平行。正确。
③ 由 $$m \perp \alpha$$ 且 $$m \parallel n$$ 得 $$n \perp \alpha$$，又 $$n \subset \beta$$，故 $$\alpha \perp \beta$$。正确。
全部正确。
答案：D
命题分析：
(1) 垂直于同一直线的两条直线可能相交、平行或异面（如长方体共顶点的三条棱）。错误。
(2) 与同一平面夹角相等的直线方向可能对称。错误。
(3) 平行于同一平面的两条直线可能平行、相交或异面。错误。
(4) 两条直线平行或相交时才确定平面。错误。
(5) 垂直于同一平面的两平面可能相交（如竖直墙壁与地板）。错误。
全部错误。
答案：A
条件分析：
A. 仅一条直线平行不足以保证直线与平面平行。错误。
B. 两条直线平行时，若它们相交则成立，但题目未说明。错误。
C. 几何关系不足以保证平行。错误。
D. 直线不在平面内且与平面内一条直线平行，则线面平行。正确。
答案：D
结论分析：
① 平行于同一平面的两直线可能相交、平行或异面。错误。
② 若 $$\alpha \parallel \beta$$ 且 $$m \perp \alpha$$，则 $$m \perp \beta$$，又 $$n \parallel \beta$$，故 $$m \perp n$$。正确。
③ 需 $$n$$ 与 $$\beta$$ 内其他直线结合才能推出 $$\alpha \perp \beta$$。错误。
④ 若 $$\alpha \perp \beta$$ 且 $$m \perp \beta$$，则 $$m \parallel \alpha$$ 或 $$m \subset \alpha$$，由 $$m \notin \alpha$$ 得 $$m \parallel \alpha$$。正确。
正确答案为②④。
答案：D
结论分析：
⊙ 缺少 $$m$$ 与 $$n$$ 相交的条件，无法推出平面垂直。错误。
⊕ 需 $$m$$ 与 $$n$$ 相交才能推出平面平行。错误。
⊙ 由 $$m \perp n$$ 且 $$n \perp \alpha$$ 得 $$m \parallel \alpha$$ 或 $$m \subset \alpha$$，结合 $$m \perp \beta$$ 可推出 $$\alpha \perp \beta$$。正确。
⊕ 缺少 $$n$$ 不在平面内的条件。错误。
仅⊙正确。
答案：B
选项分析：
A. 直线与平面垂直时，平面内所有直线与其垂直。正确。
B. 两平面垂直时，一平面内垂直于交线的直线才与另一平面垂直。错误。
C. 两直线垂直同一平面时平行。正确。
D. 两平面垂直于同一直线时可能相交。错误。
正确答案为A和C，但题目要求单选，可能为C。
答案：C