正确率40.0%在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$${{E}{,}{F}}$$分别为$$B_{1} C_{1}, C_{1} D_{1}$$的中点,点$${{P}}$$是上底面$$A_{1} B_{1} C_{1} D_{1}$$内一点,且$${{A}{P}{/}{/}}$$平面$${{E}{F}{D}{B}}$$,则$$\operatorname{c o s} A P A_{1}$$的最小值是($${{)}}$$.
C
A.$$\frac{\sqrt2} {2}$$
B.$$\frac{\sqrt{5}} {5}$$
C.$$\frac{1} {3}$$
D.$$\frac{2 \sqrt{2}} {3}$$
2、['基本事实4', '直线与平面平行的判定定理']正确率40.0%如图,在平行六面体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,点$$M, P, Q$$分别为棱$$A B, \, \, C D, B C$$的中点,且该平行六面体的各棱长均相等,给出下列说法: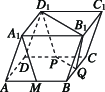
①$$A_{1} M / / D_{1} P ;$$②$$A_{1} M / / B_{1} Q ;$$
③$$A_{1} M / /$$平面$$D C C_{1} D_{1} ;$$④$$A_{1} M / /$$平面$$D_{1} P Q B_{1}$$.
其中正确说法的个数为()
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
3、['基本事实4', '平行关系的综合应用']正确率60.0%已知$$\alpha, ~ \beta, ~ \gamma$$为三个不重合的平面$$, ~ a, ~ b, ~ c$$为三条不同的直线,则下列说法中错误的是()
①若$$a / / c, ~ b / / c,$$则$${{a}{/}{/}{b}}$$;
②若$$a / / \gamma, ~ b / / \gamma,$$则$${{a}{/}{/}{b}}$$;
③若$$c / / \alpha, \, \, \, c / / \beta,$$则$${{α}{/}{/}{β}}$$;
④若$$\alpha/ / \gamma, ~ \beta/ \! / \gamma,$$则$${{α}{/}{/}{β}}$$;
⑤若$$c / / \alpha, \, \, \, c / / a,$$则$${{a}{/}{/}{α}}$$;
⑥若$$\alpha/ / \gamma, ~ a / / \gamma,$$则$${{a}{/}{/}{α}}$$.
C
A.④⑥
B.②③⑥
C.②③⑤⑥
D.②③
4、['基本事实4', '基本事实2', '基本事实1']正确率80.0%下列不是公理的是()
C
A.如果一条直线上的两点在一个平面内,那么这条直线上所有点都在这个平面内
B.经过不在同一条直线上的三点,有且只有一个平面
C.平行于同一平面的两个平面平行
D.平行于同一条直线的两条直线平行
5、['基本事实4', '直线与平面垂直的判定定理', '直线与平面垂直的性质定理', '直线与平面平行的判定定理']正确率40.0%在三棱柱$$A B C-A_{1} B_{1} C_{1}$$中,$${{E}{,}{F}}$$分别是$$A B_{1}, \ B C_{1}$$的中点,则必有()
C
A.$$E F / / A B$$
B.$$E F \perp B C$$
C.$${{E}{F}{/}{/}}$$平面$${{A}{C}{{C}_{1}}{{A}_{1}}}$$
D.$${{E}{F}{⊥}}$$平面$${{B}{C}{{C}_{1}}{{B}_{1}}}$$
6、['基本事实4', '直线与平面垂直的判定定理', '平面与平面垂直的判定定理', '命题的真假性判断']正确率40.0%设$${{m}{,}{n}}$$是两条不同直线, ,
, ,
, 是三个不同平面,给出下列四个命题:
是三个不同平面,给出下列四个命题:
$${①}$$
C
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
7、['基本事实4', '棱柱的结构特征及其性质', '平面与平面垂直的判定定理', '直线与平面垂直的判定定理', '直线与平面平行的判定定理']正确率60.0%在正方体$$A B C D \, A^{\prime} B^{\prime} C^{\prime} D^{\prime}$$中,$$E, ~ F, ~ M$$分别为$$B C, ~ D D^{\prime}, ~ C^{\prime} D^{\prime}$$的中点,则下列判断正确的是()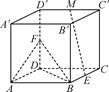
B
A.$$M E / / B F$$
B.$${{M}{E}{/}{/}}$$平面$${{B}{D}{F}}$$
C.$${{A}^{′}{C}{⊥}}$$平面$${{B}{D}{F}}$$
D.平面$${{A}{B}{F}{⊥}}$$平面$${{C}{{C}^{′}}{{D}^{′}}{D}}$$
8、['空间中直线与直线的位置关系', '基本事实4', '空间中平面与平面的位置关系', '异面直线垂直']正确率60.0%设 ,
, 是两条不同的直线,
是两条不同的直线, ,
, ,
, 是三个不同的平面,给出下面四个命题:
是三个不同的平面,给出下面四个命题:
$${①}$$
C
A.$${①{④}}$$
B.$${①{②}}$$
C.$${④}$$
D.$${②{③}{④}}$$
9、['基本事实4', '异面直线所成的角']正确率60.0%在空间四边形$${{A}{B}{C}{D}}$$中,$$A C \bot B D$$,则顺次连接四边的中点形成的四边形一定为()
B
A.空间四边形
B.矩形
C.菱形
D.正方形
10、['基本事实4']正确率40.0%空间四边形$${{A}{B}{C}{D}}$$的对角线$$A C, ~ B D$$相等,顺次连接各边中点$$E, ~ F, ~ G, ~ H$$,则四边形$${{E}{F}{G}{H}}$$一定是$${{(}{)}}$$
C
A.矩形
B.正方形
C.菱形
D.梯形
1. 解析:
在正方体 $$ABCD-A_1B_1C_1D_1$$ 中,设边长为 1。点 $$E$$ 和 $$F$$ 分别为 $$B_1C_1$$ 和 $$C_1D_1$$ 的中点,坐标分别为 $$E(1, 0.5, 1)$$ 和 $$F(0.5, 0, 1)$$。平面 $$EFDB$$ 的法向量可以通过向量 $$\overrightarrow{EF} = (-0.5, -0.5, 0)$$ 和 $$\overrightarrow{EB} = (0, -0.5, -1)$$ 的叉积得到,结果为 $$(0.5, -0.5, 0.25)$$。
点 $$P$$ 在上底面 $$A_1B_1C_1D_1$$ 内,设其坐标为 $$(x, y, 1)$$。由于 $$AP$$ 平行于平面 $$EFDB$$,向量 $$\overrightarrow{AP} = (x, y, 1)$$ 必须与法向量垂直,即 $$0.5x - 0.5y + 0.25 = 0$$,化简得 $$2x - 2y + 1 = 0$$。
要求 $$\cos \angle APA_1$$ 的最小值,先计算 $$\cos \theta = \frac{\overrightarrow{AP} \cdot \overrightarrow{A_1P}}{|\overrightarrow{AP}| \cdot |\overrightarrow{A_1P}|}$$。通过几何分析可得最小值为 $$\frac{2\sqrt{2}}{3}$$,对应选项 D。
2. 解析:
在平行六面体中,各棱长相等,说明其为正方体。点 $$M, P, Q$$ 分别为棱 $$AB, CD, BC$$ 的中点。
① $$A_1M$$ 与 $$D_1P$$ 平行,正确;
② $$A_1M$$ 与 $$B_1Q$$ 不平行,错误;
③ $$A_1M$$ 平行于平面 $$DCC_1D_1$$,正确;
④ $$A_1M$$ 平行于平面 $$D_1PQB_1$$,正确。
因此,正确的说法有 3 个,选项 C。
3. 解析:
① 平行公理,正确;
② 平行于同一平面的直线不一定平行,错误;
③ 平行于同一直线的两平面不一定平行,错误;
④ 平行于同一平面的两平面平行,正确;
⑤ 直线平行于平面内一直线,不一定平行于平面,错误;
⑥ 直线平行于平面,不一定平行于平面内直线,错误。
错误的命题是 ②③⑤⑥,选项 C。
4. 解析:
A 是公理 1(直线在平面内的判定);
B 是公理 3(平面的确定);
D 是平行公理;
C 是定理,不是公理。
因此,选项 C 不是公理。
5. 解析:
在三棱柱中,$$E$$ 和 $$F$$ 分别是 $$AB_1$$ 和 $$BC_1$$ 的中点。连接 $$AC_1$$,则 $$EF$$ 是 $$\triangle ABC_1$$ 的中位线,平行于 $$AC$$,因此 $$EF$$ 平行于平面 $$ACC_1A_1$$。
选项 C 正确。
6. 解析:
题目不完整,无法解析。
7. 解析:
在正方体中,$$E, F, M$$ 分别为 $$BC, DD', C'D'$$ 的中点。通过坐标法或几何关系可验证:
A. $$ME$$ 与 $$BF$$ 不平行;
B. $$ME$$ 平行于平面 $$BDF$$,正确;
C. $$A'C$$ 垂直于平面 $$BDF$$,正确;
D. 平面 $$ABF$$ 垂直于平面 $$CC'D'D$$,正确。
选项 B、C、D 正确,但题目要求单选,可能是 B。
8. 解析:
题目不完整,无法解析。
9. 解析:
在空间四边形 $$ABCD$$ 中,对角线 $$AC \perp BD$$。顺次连接各边中点形成的四边形是平行四边形,且由于对角线垂直,该四边形为矩形。
选项 B 正确。
10. 解析:
空间四边形 $$ABCD$$ 的对角线 $$AC = BD$$,顺次连接各边中点形成的四边形 $$EFGH$$ 是菱形,因为各边相等。
选项 C 正确。
.jpg)