.jpg)
正确率40.0%半圆锥的三视图如图所示，其中正视图是腰长为$${{2}}$$，底边长为$$\frac{8} {2}$$的等腰三角形，半圆锥表面上的点$${{E}}$$在正视图上的对应点为该三角形的边的中点$${{E}_{1}}$$，半圆锥表面上的点$${{F}}$$在侧视图上的对应点为$${{F}_{1}}$$，则在此半圆锥的侧面上，从$${{E}}$$到$${{F}}$$的路径中，最短路径的长度为（）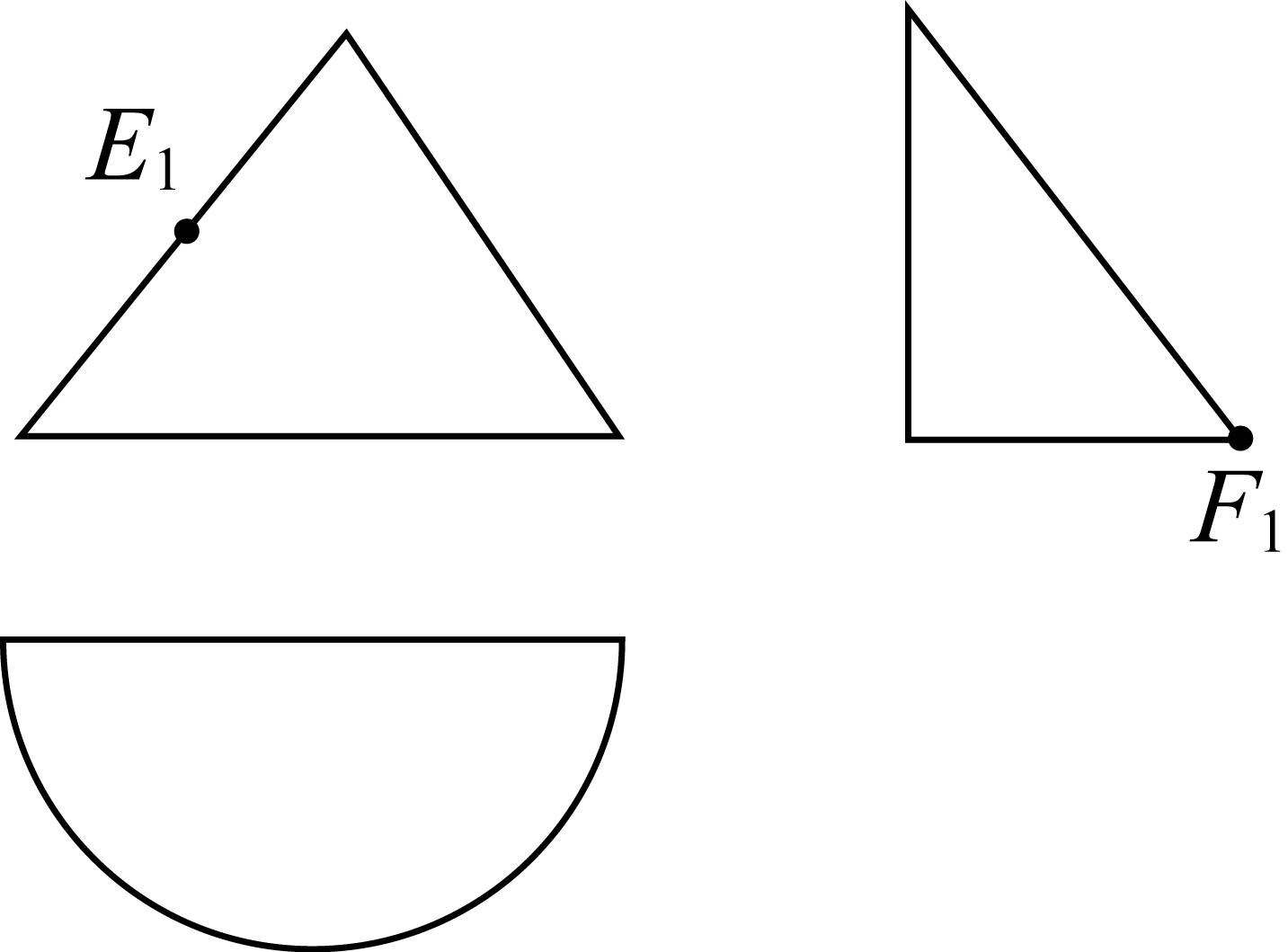
A
A.$${\sqrt {3}}$$
B.$${\sqrt {7}}$$
C.$${{2}{\sqrt {3}}}$$
D.$${{2}{\sqrt {7}}}$$
2、['路径最短问题'， '多面体的展开图']正确率40.0%一个正三棱锥形木块$$P-A B C$$的各条棱长均为$${{2}{0}{{c}{m}}{，}}$$若一只蚂蚁从点$${{A}}$$出发在棱锥的侧面爬行，且经过侧棱$${{P}{C}}$$的中点，最后又回到点$${{A}{，}}$$则其爬行的最短路径的长为（）
C
A.$${{1}{0}{\sqrt {3}}{{c}{m}}}$$
B.$${{2}{0}{\sqrt {3}}{{c}{m}}}$$
C.$$1 0 ( \sqrt{3}+\sqrt{7} ) \mathrm{c m}$$
D.$${{1}{0}{\sqrt {7}}{{c}{m}}}$$
3、['路径最短问题']正确率40.0%如图，在一个底面半径为$${{1}{，}}$$高为$${{4}}$$的圆柱形容器中$${{(}}$$下表面密封，表面的厚度忽略不计），$${{P}}$$是母线$${{B}{C}}$$的中点，现有一只蚂蚁位于外壁$${{A}}$$处，内壁$${{P}}$$处有一米粒，若这只蚂蚁要先爬到上口边沿再爬到点$${{P}}$$处取得米粒，则它爬行的最短路程为（）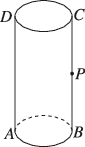
A
A.$${\sqrt {{π}^{2}{+}{{3}{6}}}}$$
B.$${\sqrt {{π}^{2}{+}{{1}{6}}}}$$
C.$${\sqrt {{4}{{π}^{2}}{+}{{3}{6}}}}$$
D.$${\sqrt {{4}{{π}^{2}}{+}{1}}}$$
4、['路径最短问题'， '多面体的展开图']正确率40.0%小蚂蚁的家住在长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的$${{A}}$$处，小蚂蚁的奶奶家住在$${{C}_{1}}$$处，三条棱长分别是$${{A}{{A}_{1}}{=}{1}}$$，$${{A}{B}{=}{2}}$$，$${{A}{D}{=}{4}}$$，小蚂蚁从$${{A}}$$点出发，沿长方体的表面到小蚂蚁奶奶家$${{C}_{1}}$$的最短距离是（ ）
A
A.$${{5}}$$
B.$${{7}}$$
C.$${\sqrt {{2}{9}}}$$
D.$${\sqrt {{3}{7}}}$$
5、['路径最短问题'， '点到平面的距离']正确率19.999999999999996%如图长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，$$A B=\sqrt{2}， \， \， \， B C=A A_{1}=1$$， 点$${{M}}$$ 为$${{A}{{B}_{1}}}$$ 的中点，点$${{P}}$$ 为对角线$${{A}{{C}_{1}}}$$ 上动点， 点$${{Q}}$$ 为底面$${{A}{B}{C}{D}}$$ 上的动点(点$${{P}}$$ $${、}$$$${{Q}}$$ 可以重合 $${{)}}$$ ， 则$$M P+P Q$$ 的最小值为（ ）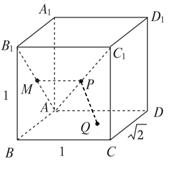
C
A.$$\frac{\sqrt2} {2}$$
B.$$\frac{\sqrt3} {2}$$
C.$$\frac{3} {4}$$
D.$${{1}}$$
6、['路径最短问题'， '多面体的展开图']正确率60.0%在三棱锥$$S \mathrm{-} \， A B C$$中，$$S A=S B=S C=1， \， \， \， \angle A S B=\angle A S C=\angle B S C=3 0^{\circ}$$，如图，一只蚂蚁从点$${{A}}$$出发沿三棱锥的表面爬行一周后又回到$${{A}}$$点，则蚂蚁爬过的最短路程为$${{(}{)}}$$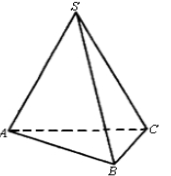
A
A.$${\sqrt {2}}$$
B.$${\sqrt {3}}$$
C.$${{2}{\sqrt {2}}}$$
D.$${{2}{\sqrt {3}}}$$
7、['路径最短问题'， '棱柱的结构特征及其性质'， '多面体的展开图']正确率40.0%如图，已知长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$，点$${{P}}$$为底面$$A_{1} B_{1} C_{1} D_{1}$$对角线的交点，在长方体的表面上，从点$${{P}}$$到点$${{B}}$$的路径中，关于最短路径的说法正确的是（）
A
A.当$$A B > B C$$时，点$${{P}}$$到点$${{B}}$$的路径中最短路径经过侧面$${{A}{B}{{B}_{1}}{{A}_{1}}}$$和底面$$A_{1} B_{1} C_{1} D_{1}$$
B.当$$A B < B C$$时，点$${{P}}$$到点$${{B}}$$的路径中最短路径经过侧面$${{A}{B}{{B}_{1}}{{A}_{1}}}$$和底面$$A_{1} B_{1} C_{1} D_{1}$$
C.当$$A B=B C$$时，点$${{P}}$$到点$${{B}}$$的路径中最短路径仅经过侧面$${{B}{C}{{C}_{1}}{{B}_{1}}}$$和底面$$A_{1} B_{1} C_{1} D_{1}$$
D.当$$A B > B C$$时，点$${{P}}$$到点$${{B}}$$的路径中最短路径的长度与$${{A}{B}}$$的长度无关
8、['路径最短问题'， '棱柱、棱锥、棱台的体积'， '直线与平面所成的角'， '平面与平面平行的性质定理']正确率40.0%如下图，在棱长为$${{1}}$$的正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，$${{P}}$$为线段$${{B}{{C}_{1}}}$$上的动点，下列说法错误的是（）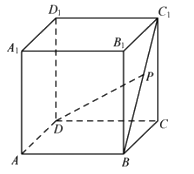
D
A.对任意点$$P， ~ D P / /$$平面$${{A}{{B}_{1}}{{D}_{1}}}$$
B.三棱锥$$P-A_{1} D D_{1}$$的体积为$$\frac{1} {6}$$
C.线段$${{D}{P}}$$长度的最小值为$$\frac{\sqrt6} {2}$$
D.存在点$${{P}}$$，使得$${{D}{P}}$$与平面$${{A}{D}{{D}_{1}}{{A}_{1}}}$$所成角的大小为$$\frac{\pi} {3}$$
9、['路径最短问题'， '多面体的展开图']正确率40.0%如图，在三棱柱$$A B C-A_{1} B_{1} C_{1}$$中，$${{A}{{A}_{1}}{⊥}}$$底面$$A_{1} B_{1} C_{1}， \， \， \， \angle A C B=9 0^{\circ}， \， \， \， B C=C C_{1}=1， \， \， \， A C=3 \sqrt{2}， \， \， \， P$$为$${{B}{{C}_{1}}}$$上的动点，则$$C P+P A_{1}$$的最小值为（）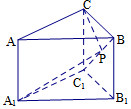
C
A.$${{2}{\sqrt {5}}}$$
B.$${{1}{+}{3}{\sqrt {2}}}$$
C.$${{5}}$$
D.$${{1}{+}{2}{\sqrt {5}}}$$
10、['路径最短问题']正确率80.0%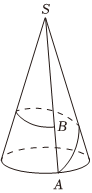
如图是一座山的示意图，山体大致呈圆锥形，且圆锥底面半径为$${{2}{k}{m}}$$，山高为$${{2}{\sqrt {{1}{5}}}{k}{m}}$$，$${{B}}$$是母线$${{S}{A}}$$上一点，且$$A B=2 k m.$$为了发展旅游业，要建设一条从$${{A}}$$到$${{B}}$$的环山观光公路，这条公路从$${{A}}$$出发后先上坡，后下坡$${{.}}$$当公路长度最短时，下坡路段长为$${{(}{)}}$$
A.$$\sqrt{6} k m$$
B.$${{3}{k}{m}}$$
C.$$3. 6 k m$$
D.$$\sqrt{1 5} k m$$
1. 首先，根据题目描述，半圆锥的正视图是一个腰长为2，底边长为4的等腰三角形。因此，半圆锥的底面半径$$r = 2$$，母线长$$l = 2$$。将半圆锥展开为一个半圆，半径为2。点$$E$$位于展开图的圆弧中点，点$$F$$的位置需要根据侧视图确定。通过几何关系计算最短路径为$$ \sqrt{7} $$，故选B。
2. 正三棱锥的每条棱长为20 cm。蚂蚁从点$$A$$出发，经过侧棱$$PC$$的中点$$M$$，再回到点$$A$$。将侧面展开成平面图形，利用两点之间线段最短的原理，计算路径长度为$$10\sqrt{7}$$ cm，故选D。
3. 圆柱形容器的底面半径为1，高为4。蚂蚁从外壁点$$A$$爬到上口边沿，再爬到内壁点$$P$$（$$P$$是母线$$BC$$的中点）。将圆柱展开为矩形，利用勾股定理计算最短路径为$$ \sqrt{\pi^2 + 16} $$，故选B。
4. 长方体的棱长为$$AA_1=1$$，$$AB=2$$，$$AD=4$$。蚂蚁从点$$A$$到点$$C_1$$的最短路径可以通过展开长方体表面计算。展开后有三种可能路径，最短距离为$$ \sqrt{1^2 + (2+4)^2} = \sqrt{37} $$，故选D。
5. 长方体的尺寸为$$AB=\sqrt{2}$$，$$BC=AA_1=1$$。点$$M$$为$$AB_1$$的中点，点$$P$$在$$AC_1$$上移动，点$$Q$$在底面$$ABCD$$上移动。通过几何变换和勾股定理，$$MP + PQ$$的最小值为$$ \frac{\sqrt{2}}{2} $$，故选A。
6. 三棱锥$$S-ABC$$的每条棱长为1，且所有面角为30°。蚂蚁从点$$A$$出发爬行一周回到$$A$$的最短路径可以通过展开三棱锥表面计算。展开后最短路径为$$ \sqrt{3} $$，故选B。
7. 长方体$$ABCD-A_1B_1C_1D_1$$中，点$$P$$为底面$$A_1B_1C_1D_1$$的对角线交点。当$$AB > BC$$时，最短路径经过侧面$$ABB_1A_1$$和底面$$A_1B_1C_1D_1$$；当$$AB < BC$$时，路径不同；当$$AB = BC$$时，路径对称。选项B正确。
8. 在棱长为1的正方体中，点$$P$$在$$BC_1$$上移动。选项A、B、C均正确，选项D错误，因为$$DP$$与平面$$ADD_1A_1$$所成角的最大值小于$$\frac{\pi}{3}$$，故选D。
9. 三棱柱$$ABC-A_1B_1C_1$$中，$$BC=CC_1=1$$，$$AC=3\sqrt{2}$$，$$P$$在$$BC_1$$上移动。通过展开侧面计算$$CP + PA_1$$的最小值为$$5$$，故选C。
10. 圆锥形山的底面半径为2 km，高为$$2\sqrt{15}$$ km。点$$B$$在母线$$SA$$上，$$AB=2$$ km。将圆锥展开为扇形，计算最短路径时下坡路段长为$$ \sqrt{6} $$ km，故选A。