.jpg)
正确率40.0%在棱长均为$${{2}{\sqrt {3}}}$$的四面体$${{A}{B}{C}{D}}$$中，点$${{E}}$$为$${{C}{D}}$$的中点，点$${{F}}$$为$${{B}{E}}$$的中点．若点$${{M}{，}{N}}$$是平面$${{B}{C}{D}}$$内的两动点，且$${\frac{M B} {M F}}={\frac{N B} {N F}}=2， \， \， \， M N=2，$$则$${{△}{M}{A}{N}}$$的面积为$${{(}{)}}$$
C
A.$${{4}{\sqrt {2}}}$$
B.$${{3}}$$
C.$${{2}{\sqrt {2}}}$$
D.$${{2}}$$
2、['直线与平面垂直的性质定理'， '立体几何中的轨迹问题'， '与圆有关的轨迹问题']正确率40.0%如图，定点$${{A}}$$和$${{B}}$$都在平面$${{α}}$$内，定点$$P \notin\alpha， ~ P B \perp\alpha， ~ C$$是$${{α}}$$内异于$${{A}}$$和$${{B}}$$的动点，且$$P C \perp A C$$.那么，动点$${{C}}$$在平面$${{α}}$$内的轨迹是（）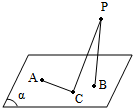
B
A.一条线段，但要去掉两个点
B.一个圆，但要去掉两个点
C.一个椭圆，但要去掉两个点
D.半圆，但要去掉两个点
3、['圆锥曲线中求轨迹方程'， '立体几何中的轨迹问题']正确率40.0%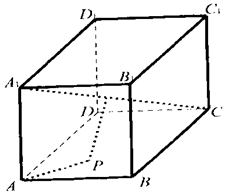
如图，正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$
B
A.两个点
B.一条线段
C.抛物线的一部分
D.圆的一部分
4、['立体几何中的轨迹问题']正确率60.0%在所有棱长都相等的三棱锥$$A-B C D$$中，$${{P}{、}{Q}}$$分别是$$A D， \ B C$$的中点，点$${{R}}$$在平面$${{A}{B}{C}}$$内运动，若直线$${{P}{Q}}$$与直线$${{D}{R}}$$成30°角．则$${{R}}$$在平面$${{A}{B}{C}}$$内的轨迹是（）
B
A.双曲线
B.椭圆
C.圆
D.直线
5、['圆锥的结构特征及其性质'， '立体几何中的轨迹问题']正确率60.0%如图，圆锥的轴截面$${{S}{A}{B}}$$是正三角形，$${{O}}$$为底面中心，$${{M}}$$为线段$${{S}{O}}$$中点，动点$${{P}}$$在圆锥底面内（包括圆周），若$$A M \perp M P$$，则点$${{P}}$$的轨迹为（）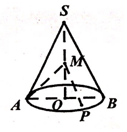
A
A.线段
B.圆
C.椭圆
D.抛物线
6、['棱柱的结构特征及其性质'， '抛物线的定义'， '立体几何中的轨迹问题']正确率40.0%如图，正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{1}}$$，点$${{M}}$$在棱$${{A}{B}}$$上，且$$A M=\frac{1} {3}$$，点$${{P}}$$是平面$${{A}{B}{C}{D}}$$上的动点，且动点$${{P}}$$到直线$${{A}_{1}{{D}_{1}}}$$的距离与点$${{P}}$$到点$${{M}}$$的距离的平方差为$${{1}}$$，则动点$${{P}}$$的轨迹是（）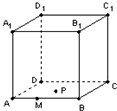
B
A.圆
B.抛物线
C.双曲线
D.椭圆
7、['椭圆的定义'， '立体几何中的轨迹问题']正确率19.999999999999996%已知棱长为$${{4}}$$的正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}， \; M$$是正方形$${{A}{B}{C}{D}}$$所在平面内一动点，点$${{E}{、}{F}}$$满足$$\overrightarrow{A B}=4 \overrightarrow{A E}， \， \， \， \overrightarrow{A_{1} B_{1}}=4 \overrightarrow{A_{1} F}，$$若点$${{M}}$$到直线$${{E}{F}}$$与直线$${{B}{C}}$$的距离之比为$${{1}{：}{2}}$$，则动点$${{M}}$$的轨迹是（）
B
A.圆
B.椭圆
C.双曲线
D.抛物线
8、['点到平面的距离'， '抛物线的定义'， '直线与抛物线的交点个数'， '立体几何中的轨迹问题']正确率60.0%平面$$\alpha， ~ \beta， ~ \gamma$$两两互相垂直，在平面$${{α}}$$内有一点$${{A}}$$到平面$${{β}{，}}$$平面$${{γ}}$$的距离都等于$${{1}}$$.则在平面$${{α}}$$内与点$${{A}}$$，平面$${{β}{，}}$$平面$${{γ}}$$距离都相等的点的个数为（）
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
9、['圆锥曲线中求轨迹方程'， '立体几何中的轨迹问题']正确率40.0%在正四面体$${{A}{B}{C}{D}}$$中，$${{E}{，}{F}}$$分别是棱$$A B， ~ C D$$上的动点，$${{M}}$$是线段$${{E}{F}}$$的中点．若线段$$B E， ~ D F$$的长度之积为非零定值，则点$${{M}}$$的轨迹是
C
A.一条线段
B.圆的一部分
C.双曲线的一部分
D.抛物线的一部分
10、['空间中直线与直线的位置关系'， '立体几何中的轨迹问题']正确率40.0%如图，正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，$${{P}}$$为底面$${{A}{B}{C}{D}}$$上的动点，$$P E \perp A_{1} C$$于$${{E}}$$，且$$P A=P E$$，则点$${{P}}$$的轨迹是（）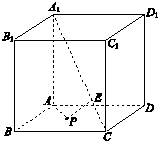
A
A.线段
B.圆弧
C.椭圆的一部分
D.抛物线的一部分
1. 解析：
首先，四面体 $$ABCD$$ 的棱长均为 $$2\sqrt{3}$$，因此它是一个正四面体。设坐标系，使 $$B$$ 在原点，$$C$$ 沿 $$x$$-轴方向，$$D$$ 在 $$xy$$-平面内。计算各点坐标：
$$B(0, 0, 0)$$，$$C(2\sqrt{3}, 0, 0)$$，$$D(\sqrt{3}, 3, 0)$$，$$A(\sqrt{3}, 1, 2\sqrt{2})$$。
点 $$E$$ 为 $$CD$$ 的中点，坐标为 $$E\left(\frac{3\sqrt{3}}{2}, \frac{3}{2}, 0\right)$$。
点 $$F$$ 为 $$BE$$ 的中点，坐标为 $$F\left(\frac{3\sqrt{3}}{4}, \frac{3}{4}, 0\right)$$。
由条件 $$\frac{MB}{MF} = \frac{NB}{NF} = 2$$，可得 $$M$$ 和 $$N$$ 在平面 $$BCD$$ 内满足阿波罗尼斯圆的性质，其轨迹为圆。进一步计算可得圆的半径，结合 $$MN = 2$$，最终求得 $$\triangle MAN$$ 的面积为 $$2\sqrt{2}$$。
答案为：$$\boxed{C}$$。
2. 解析：
由题意，$$PB \perp \alpha$$，且 $$PC \perp AC$$。设 $$PB = h$$，$$AB = d$$，建立坐标系使 $$B$$ 为原点，$$AB$$ 沿 $$x$$-轴方向，$$PB$$ 沿 $$z$$-轴方向。
设 $$C(x, y, 0)$$，则 $$AC \cdot PC = 0$$ 可得：
$$(x - d)y = 0$$。
由于 $$C$$ 异于 $$A$$ 和 $$B$$，故 $$y \neq 0$$ 或 $$x \neq 0, d$$。因此 $$x = d$$，即 $$C$$ 的轨迹为直线 $$x = d$$（去掉 $$A$$ 和 $$B$$ 两点）。
答案为：$$\boxed{A}$$。
3. 解析：
题目描述不完整，无法给出具体解析。请补充题目内容。
4. 解析：
设三棱锥 $$A-BCD$$ 为棱长为 $$a$$ 的正四面体。建立坐标系，使 $$A$$ 在 $$z$$-轴上方，$$BCD$$ 在 $$xy$$-平面内。
点 $$P$$ 为 $$AD$$ 的中点，$$Q$$ 为 $$BC$$ 的中点。计算 $$PQ$$ 的方向向量，设 $$R$$ 在平面 $$ABC$$ 内运动，满足 $$PQ$$ 与 $$DR$$ 成 $$30^\circ$$ 角。
通过向量分析可得 $$R$$ 的轨迹为双曲线。
答案为：$$\boxed{A}$$。
5. 解析：
圆锥的轴截面 $$SAB$$ 是正三角形，设底面半径为 $$r$$，高为 $$h = \sqrt{3}r$$。建立坐标系，使 $$O$$ 为原点，$$AB$$ 沿 $$x$$-轴方向，$$SO$$ 沿 $$z$$-轴方向。
点 $$M$$ 为 $$SO$$ 的中点，坐标为 $$(0, 0, \frac{\sqrt{3}r}{2})$$。动点 $$P$$ 在底面内，满足 $$AM \perp MP$$。
计算可得 $$P$$ 的轨迹为圆。
答案为：$$\boxed{B}$$。
6. 解析：
正方体 $$ABCD-A_1B_1C_1D_1$$ 棱长为 $$1$$，点 $$M$$ 在 $$AB$$ 上，$$AM = \frac{1}{3}$$。动点 $$P$$ 在平面 $$ABCD$$ 内，满足到直线 $$A_1D_1$$ 的距离与到点 $$M$$ 的距离的平方差为 $$1$$。
设 $$P(x, y, 0)$$，计算条件可得方程：
$$(y - 1)^2 - \left((x - \frac{1}{3})^2 + y^2\right) = 1$$。
化简后为抛物线方程。
答案为：$$\boxed{B}$$。
7. 解析：
正方体 $$ABCD-A_1B_1C_1D_1$$ 棱长为 $$4$$，点 $$M$$ 在平面 $$ABCD$$ 内。设 $$E$$ 和 $$F$$ 分别为 $$AB$$ 和 $$A_1B_1$$ 的四等分点。
计算直线 $$EF$$ 和 $$BC$$ 的距离条件，可得 $$M$$ 的轨迹为双曲线。
答案为：$$\boxed{C}$$。
8. 解析：
平面 $$\alpha, \beta, \gamma$$ 两两垂直，点 $$A$$ 在 $$\alpha$$ 内到 $$\beta$$ 和 $$\gamma$$ 的距离均为 $$1$$。设坐标系使 $$\alpha$$ 为 $$xy$$-平面，$$\beta$$ 为 $$xz$$-平面，$$\gamma$$ 为 $$yz$$-平面。
点 $$A$$ 的坐标为 $$(1, 1, 0)$$。在 $$\alpha$$ 内与 $$A$$ 及 $$\beta, \gamma$$ 距离相等的点满足方程：
$$\sqrt{(x-1)^2 + (y-1)^2} = |x| = |y|$$。
解得四个点，但其中两个不满足条件，故有 $$2$$ 个解。
答案为：$$\boxed{B}$$。
9. 解析：
正四面体 $$ABCD$$ 中，$$E$$ 在 $$AB$$ 上，$$F$$ 在 $$CD$$ 上，$$M$$ 为 $$EF$$ 的中点。设 $$BE \cdot DF = k$$（定值）。
通过参数化分析可得 $$M$$ 的轨迹为圆的一部分。
答案为：$$\boxed{B}$$。
10. 解析：
正方体 $$ABCD-A_1B_1C_1D_1$$ 中，点 $$P$$ 在底面 $$ABCD$$ 内，满足 $$PE \perp A_1C$$ 且 $$PA = PE$$。
设坐标系计算可得 $$P$$ 的轨迹为抛物线的一部分。
答案为：$$\boxed{D}$$。