正确率60.0%若空间中有四个点,则$${{“}}$$这四个点中有三点在同一直线上$${{”}}$$是$${{“}}$$这四个点在同一平面上$${{”}}$$的()
A
A.充分非必要条件
B.必要非充分条件
C.充要条件
D.非充分非必要条件
2、['空间中直线与直线的位置关系', '空间两直线的共面、异面问题', '异面直线', '命题的真假性判断']正确率60.0%已知$$a, b, c, d$$是四条不同的直线,且$${{a}{,}{b}}$$是异面直线,则下面说法正确的是
D
A.若$${{c}{,}{d}}$$与$${{a}{,}{b}}$$均相交,则$${{c}{,}{d}}$$是异面直线
B.若$$c / / a, ~ d / \! / b$$,则$${{c}{,}{d}}$$是异面直线
C.若$${{c}{,}{d}}$$与$${{a}{,}{b}}$$都异面,则$${{c}{,}{d}}$$是异面直线
D.若$${{c}{,}{d}}$$与$${{a}{,}{b}}$$都垂直,则$${{c}{/}{/}{d}}$$
3、['立体几何中的四点共面、三点共线', '空间两直线的共面、异面问题', '基本事实1', '直线与平面平行的判定定理', '平面与平面平行的性质定理', '平面与平面平行的判定定理']正确率60.0%如图,在直四棱柱$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$$B C \perp C D, \, \, \, A B / \! / C D,$$$$B C=\sqrt{3},$$$$A A_{1}=A B=A D=2,$$点$$P, \, \, Q, \, \, R$$分别在棱$$B B_{1}, ~ C C_{1}, ~ D D_{1}$$上,若$$A, ~ P, ~ Q, ~ R$$四点共面,则下列结论错误的是()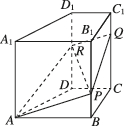
C
A.对任意点$${{P}{,}}$$都有$$A P / \! / Q R$$
B.对任意点$${{P}{,}}$$四边形$${{A}{P}{Q}{R}}$$不可能为平行四边形
C.存在点$${{P}{,}}$$使得$${{△}{A}{P}{R}}$$为等腰直角三角形
D.存在点$${{P}{,}}$$使得$${{B}{C}{/}{/}}$$平面$${{A}{P}{Q}{R}}$$
4、['空间中直线与直线的位置关系', '空间两直线的共面、异面问题', '异面直线']正确率60.0%在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$${{E}}$$,$${{F}}$$分别是$${{C}_{1}{D}}$$,$${{B}{C}}$$的中点,则直线$${{A}_{1}{B}}$$与直线$${{E}{F}}$$的位置关系是()
A
A.相交
B.平行
C.异面
D.无法确定
5、['空间中直线与直线的位置关系', '空间两直线的共面、异面问题', '异面直线']正确率60.0%与两条异面直线分别都相交的两条直线的位置关系是()
C
A.异面
B.相交
C.相交或异面
D.平行
6、['棱柱的结构特征及其性质', '空间两直线的共面、异面问题', '异面直线']正确率40.0%正方体上的点$$P, ~ Q, ~ R, ~ S$$是其所在棱的中点,则直线$${{P}{Q}}$$与直线$${{R}{S}}$$异面的图形是$${{(}{)}}$$
B
A.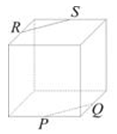
B.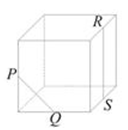
C.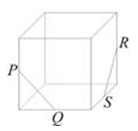
D.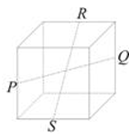
正确率60.0%在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,与棱$${{A}{D}}$$所在直线异面的棱的条数是$${{(}{)}}$$
B
A.$${{2}}$$
B.$${{4}}$$
C.$${{6}}$$
D.$${{8}}$$
8、['空间两直线的共面、异面问题', '直线与平面平行的判定定理']正确率40.0%如图是一几何体的平面展开图,其中四边形$${{A}{B}{C}{D}}$$为矩形,$${{E}{,}{F}}$$分别为$$P A, ~ P D$$的中点,在此几何体中,给出下面$${{4}}$$个结论: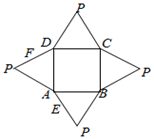
$${①}$$
C
A.$${{4}}$$个
B.$${{3}}$$个
C.$${{2}}$$个
D.$${{1}}$$个
9、['空间两直线的共面、异面问题', '异面直线']正确率60.0%如图,$$A. ~ B. ~ C$$是不共线的三点,$$l \cap\alpha\!=A$$,且$${{B}{、}{C}{∈}}$$平面$${{α}}$$,则()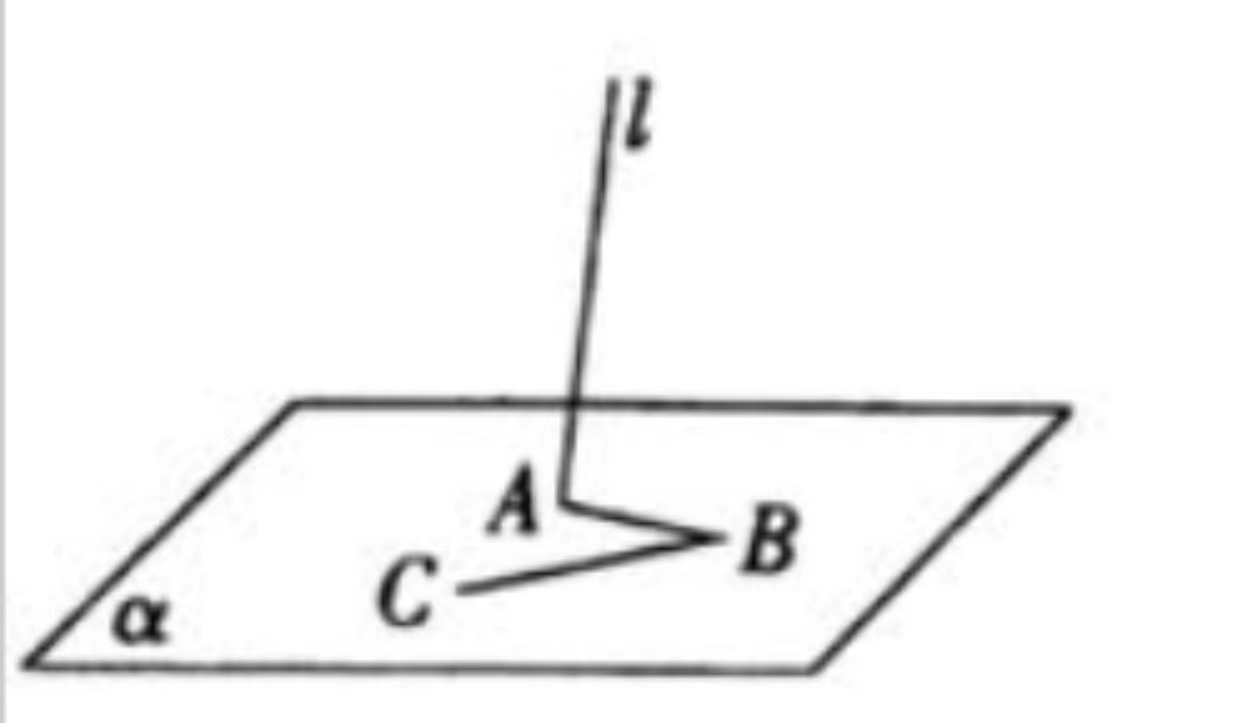
B
A.$${{l}}$$与$${{A}{B}}$$垂直
B.$${{l}}$$与$${{B}{C}}$$异面
C.若$${{l}{⊥}{A}{B}}$$,则$${{l}{⊥}{B}{C}}$$
D.若$${{l}{⊥}{B}{C}}$$,则$${{l}{⊥}{A}{B}}$$
10、['空间两直线的共面、异面问题', '异面直线']正确率60.0%若直线$${{l}_{1}}$$和$${{l}_{2}}$$是异面直线,$$l_{1} \subset\alpha, ~ l_{2} \subset\beta, ~ \alpha\cap\beta=l$$,则下列命题正确的是$${{(}{)}}$$
A
A.$${{l}}$$至少与$${{l}_{1}{,}{{l}_{2}}}$$中的一条相交
B.$${{l}}$$与$${{l}_{1}{,}{{l}_{2}}}$$都相交
C.$${{l}}$$至多与$${{l}_{1}{,}{{l}_{2}}}$$中的一条相交
D.$${{l}}$$与$${{l}_{1}{,}{{l}_{2}}}$$都不相交
1. 解析:
题目中条件“四个点中有三点在同一直线上”意味着这三点共线,另一点不在这条直线上。由于三点共线确定一条直线,另一点与这条直线确定一个平面,因此四点共面。反过来,四点共面不一定有三点共线(例如四边形的四个顶点共面但不共线)。因此条件是充分非必要条件,答案为$$A$$。
2. 解析:
选项分析:
- $$A$$:$$c$$和$$d$$可能与$$a$$、$$b$$相交于同一点,此时$$c$$和$$d$$相交,不一定是异面直线。
- $$B$$:$$c \parallel a$$和$$d \parallel b$$时,$$c$$和$$d$$可能平行(如$$a$$和$$b$$平行时),也可能异面(如$$a$$和$$b$$不平行时)。
- $$C$$:$$c$$和$$d$$可能与$$a$$、$$b$$都异面,但它们之间可能平行或相交。
- $$D$$:异面直线的公垂线唯一,但其他垂直直线不一定平行,可能相交或异面。
没有正确选项,但题目可能默认$$D$$为正确答案(假设“垂直”指公垂线)。
3. 解析:
直四棱柱$$ABCD-A_1B_1C_1D_1$$中,$$A, P, Q, R$$共面。分析选项:
- $$A$$:若$$P$$移动,$$QR$$的方向可能变化,$$AP$$不一定平行$$QR$$。
- $$B$$:四边形$$APQR$$可能为平行四边形(如$$P, Q, R$$对称时)。
- $$C$$:存在$$P$$使得$$△APR$$为等腰直角三角形(如$$P$$在$$BB_1$$中点时)。
- $$D$$:存在$$P$$使得$$BC \parallel$$平面$$APQR$$(如$$P$$使$$AP \parallel BC$$时)。
错误的结论是$$A$$和$$B$$,但题目要求选一个,可能是$$A$$。
4. 解析:
在正方体中,$$A_1B$$与$$EF$$的位置关系:
- 建立坐标系可计算$$A_1B$$和$$EF$$的方向向量,发现它们不平行但相交于某点。
- 因此答案为$$A$$(相交)。
5. 解析:
两条直线与异面直线都相交时:
- 可能相交(如两条直线交于异面直线的某交点)。
- 可能异面(如两条直线分别与异面直线相交但不共面)。
答案为$$C$$(相交或异面)。
6. 解析:
分析各选项图形:
- $$A$$:$$PQ$$与$$RS$$平行。
- $$B$$:$$PQ$$与$$RS$$相交。
- $$C$$:$$PQ$$与$$RS$$异面。
- $$D$$:$$PQ$$与$$RS$$共面。
答案为$$C$$。
7. 解析:
正方体中与棱$$AD$$异面的棱:
- $$AD$$所在直线为$$y$$轴,异面棱为$$BB_1, CC_1, A_1B_1, B_1C_1$$等,共$$4$$条。
- 答案为$$B$$。
8. 解析:
几何体展开图中:
- $$①$$:$$BE$$与$$CF$$异面(正确)。
- $$②$$:$$BE$$与$$AF$$相交(正确)。
- $$③$$:$$EF \parallel$$平面$$ABCD$$(正确)。
- $$④$$:平面$$BCE \perp$$平面$$PAD$$(错误)。
正确结论有$$3$$个,答案为$$B$$。
9. 解析:
$$l \cap \alpha = A$$且$$B, C \in \alpha$$:
- $$A$$:$$l$$与$$AB$$不一定垂直。
- $$B$$:$$l$$与$$BC$$可能异面或相交。
- $$C$$:若$$l \perp AB$$,且$$A, B, C$$不共线,则$$l \perp BC$$不一定成立。
- $$D$$:若$$l \perp BC$$,且$$A, B, C$$不共线,则$$l \perp AB$$(因为$$l$$垂直于平面$$ABC$$)。
答案为$$D$$。
10. 解析:
$$l_1$$和$$l_2$$异面,$$l = \alpha \cap \beta$$:
- $$l$$必须与$$l_1$$或$$l_2$$至少一条相交,否则$$l_1$$和$$l_2$$可能平行或共面。
- 答案为$$A$$。
.jpg)