正确率40.0%在长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$$A B=5, \, \, \, A D=4, \, \, \, A A_{1}=3,$$以$${{D}}$$为原点,$$D A, ~ D C, ~ D D_{1}$$所在直线分别为$${{x}}$$轴、$${{y}}$$轴、$${{z}}$$轴,建立如图所示的空间直角坐标系$$D x y z,$$则下列结论中不正确的是()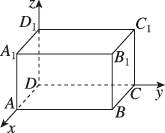
C
A.点$${{A}}$$关于直线$${{D}{{D}_{1}}}$$对称的点为$$(-4, ~ 0, ~ 0 )$$
B.点$${{C}_{1}}$$关于点$${{B}}$$对称的点为$$( 8, ~ 5, ~-3 )$$
C.点$${{B}_{1}}$$的坐标为$$( 3, ~ 5, ~ 4 )$$
D.点$${{C}}$$关于平面$${{A}{B}{{B}_{1}}{{A}_{1}}}$$对称的点为$$( 8, ~ 5, ~ 0 )$$
2、['立体几何位置关系的综合应用', '平面的法向量及其应用']正确率60.0%已知$${{n}}$$为平面$${{α}}$$的一个法向量$${,{l}}$$为一条直线,则“$${{l}{⊥}{n}}$$”是“$${{l}{/}{/}{α}}$$”的()
B
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分又不必要条件
3、['立体几何位置关系的综合应用']正确率60.0%已知$${{m}{,}{n}}$$为两条不同的直线$${,{α}{,}{β}}$$为两个不同的平面,给出下列说法:
①若$$m / / \alpha, ~ \alpha/ / \beta,$$则$${{m}{/}{/}{β}}$$;②若$$m / / \alpha, ~ m / / \beta,$$则$${{α}{/}{/}{β}}$$;
③若$$m \perp\alpha, \, \, n \perp\beta, \, \, \alpha/ \! / \beta,$$则$${{m}{/}{/}{n}}$$;④若$$m \perp\alpha, \, n \perp\beta, \, \, \alpha\perp\beta,$$则$${{m}{⊥}{n}}$$.
其中正确说法的个数为()
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
4、['空间中直线与直线的位置关系', '立体几何位置关系的综合应用', '空间中直线与平面的位置关系']正确率60.0%已知直线$${{l}{,}{m}}$$和平面$${{α}{,}}$$则下列命题中正确的是()
B
A.若$$l / \! / m, ~ m$$$${{⊂}{a}{,}}$$则$${{l}{/}{/}{α}}$$
B.若$$l \perp\alpha, m$$$${{⊂}{a}{,}}$$则$${{l}{⊥}{m}}$$
C.若$$l \perp m, \; l \perp\alpha$$则$${{m}{⊥}{α}}$$
D.若$$l / \! / \alpha, m$$$${{⊂}{a}{,}}$$则$${{l}{/}{/}{m}}$$
5、['立体几何位置关系的综合应用']正确率40.0%已知直线$${{l}{,}{m}}$$和平面$${{α}{,}}$$下列说法正确的是()
D
A.若$$l / / \alpha, ~ m \subset\alpha$$,则$${{l}{/}{/}{m}}$$
B.若$$l / / m, ~ m \subset\alpha$$,则$${{l}{/}{/}{α}}$$
C.若$$l \perp m, ~ m \subset\alpha$$,则$${{l}{⊥}{α}}$$
D.若$$l \perp\alpha, ~ m \subset\alpha$$,则$${{l}{⊥}{m}}$$
6、['立体几何位置关系的综合应用', '二面角']正确率40.0%已知$${{△}{A}{B}{C}}$$得内角$$A, ~ B, ~ C$$所对的边分别为$$a, ~ b, ~ c$$,且$$a < b < c, \, \, \, P$$点在$${{△}{A}{B}{C}}$$所在平面上的投影恰好是$${{△}{A}{B}{C}}$$的重心$${{G}}$$,设平面$$P A B, ~ P A C, ~ P C B$$与底面$${{A}{B}{C}}$$所成的锐二面角分别为$$\alpha, ~ \beta, ~ \gamma,$$则()
A
A.$$\alpha> \beta> \gamma$$
B.$$\alpha< \beta< \gamma$$
C.$$\alpha=\beta=\gamma$$
D.$$\alpha< \gamma< \beta$$
7、['立体几何位置关系的综合应用', '空间中直线与直线的位置关系', '空间中直线与平面的位置关系', '空间中平面与平面的位置关系', '命题的真假性判断']正确率60.0%已知直线$${{m}{,}{n}}$$,平面$${{α}{,}{β}{,}}$$且$$m \bot\alpha, ~ n \subset\beta$$,则以下命题:
$${①}$$若$$\alpha/ / \beta,$$则$${{m}{⊥}{n}}$$;
$${②}$$若$${{α}{⊥}{β}{,}}$$则$${{m}{/}{/}{n}}$$;
$${③}$$若$${{m}{⊥}{n}}$$,则$${{α}{⊥}{β}{;}}$$
$${④}$$若$${{m}{/}{/}{n}}$$,则$${{α}{⊥}{β}{.}}$$其中正确的个数是()
B
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
8、['立体几何位置关系的综合应用']正确率40.0%已知$${{m}{,}{n}}$$是两条不重合的直线,$${{α}{,}{β}}$$是不重合的平面,下面四个命题中正确的是()
D
A.若$$m \subseteq\alpha, ~ n \, / / \alpha$$,则$${{m}{/}{/}{n}}$$
B.若$$m \bot n, ~ m \bot\beta$$,则$${{n}{/}{/}{β}}$$
C.若$$\alpha\bigcap\beta=n, \, \, \, m \, / \! / n$$,则$${{m}{/}{/}{α}}$$且$${{m}{/}{/}{β}}$$
D.若$$m \perp\alpha, ~ m \perp\beta$$,则$${{α}{/}{/}{β}}$$
9、['立体几何位置关系的综合应用']正确率40.0%设$${{m}{,}{n}}$$是两条不同的直线, ,
, 是两个不同的平面,则下列命题中不正确的是$${{(}{)}}$$
是两个不同的平面,则下列命题中不正确的是$${{(}{)}}$$
A
A.若 ,
, ,
, ,则
,则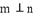
B.若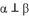 ,
,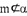 ,
,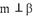 ,则
,则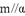
C.若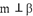 ,
, ,则
,则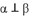
D.若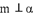 ,
,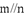 ,
,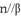 ,则
,则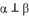
正确率40.0%$$l. ~ m. ~ n$$是三条不同的直线,$${{α}{、}{β}}$$为两个不同的平面,下列说法正确的是()
C
A.若$$l / / \alpha, ~ l / / \beta$$,则$${{α}{/}{/}{β}}$$
B.若$$l \bot m, ~ l \bot n$$,则$${{m}{⊥}{n}}$$
C.若$$l / / m, ~ l \bot\alpha$$,则$${{m}{⊥}{α}}$$
D.若$${{l}{、}{m}}$$与$${{α}}$$所成的角相等,则$${{l}{/}{/}{m}}$$
1. 在长方体$$ABCD-A_1B_1C_1D_1$$中,建立坐标系后,各点坐标为:$$A(4,0,0)$$,$$C(0,5,0)$$,$$C_1(0,5,3)$$,$$B(4,5,0)$$,$$B_1(4,5,3)$$。
A. 点$$A$$关于直线$$DD_1$$对称的点为$$(-4,0,0)$$,正确,因为对称操作仅改变$$x$$坐标符号。
B. 点$$C_1$$关于点$$B$$对称的点为$$(8,5,-3)$$,计算过程为$$(2 \times 4 - 0, 2 \times 5 - 5, 2 \times 0 - 3)$$,题目中给出的是$$(8,5,-3)$$,但选项为$$(8,5,-3)$$,因此正确。
C. 点$$B_1$$的坐标为$$(4,5,3)$$,题目中给出$$(3,5,4)$$错误。
D. 点$$C$$关于平面$$ABB_1A_1$$对称的点为$$(8,5,0)$$,因为平面$$ABB_1A_1$$的方程为$$x=4$$,对称操作后$$x$$坐标为$$2 \times 4 - 0 = 8$$,其他坐标不变,正确。
综上,不正确的是选项C。
2. 若$$l \perp n$$,则$$l$$平行于平面$$\alpha$$或$$l$$在平面$$\alpha$$内;反之,若$$l \parallel \alpha$$,则$$l$$与法向量$$n$$垂直。因此,“$$l \perp n$$”是“$$l \parallel \alpha$$”的必要不充分条件,选B。
3. 分析各命题:
① 若$$m \parallel \alpha$$,$$\alpha \parallel \beta$$,则$$m \parallel \beta$$或$$m \subset \beta$$,错误。
② 若$$m \parallel \alpha$$,$$m \parallel \beta$$,则$$\alpha \parallel \beta$$或$$\alpha$$与$$\beta$$相交,错误。
③ 若$$m \perp \alpha$$,$$n \perp \beta$$,$$\alpha \parallel \beta$$,则$$m \parallel n$$,正确。
④ 若$$m \perp \alpha$$,$$n \perp \beta$$,$$\alpha \perp \beta$$,则$$m \perp n$$或$$m$$与$$n$$相交,错误。
只有③正确,选A。
4. 分析各选项:
A. 若$$l \parallel m$$,$$m \subset \alpha$$,则$$l \parallel \alpha$$或$$l \subset \alpha$$,错误。
B. 若$$l \perp \alpha$$,$$m \subset \alpha$$,则$$l \perp m$$,正确。
C. 若$$l \perp m$$,$$l \perp \alpha$$,则$$m \parallel \alpha$$或$$m \subset \alpha$$,错误。
D. 若$$l \parallel \alpha$$,$$m \subset \alpha$$,则$$l \parallel m$$或$$l$$与$$m$$异面,错误。
选B。
5. 分析各选项:
A. 若$$l \parallel \alpha$$,$$m \subset \alpha$$,则$$l \parallel m$$或异面,错误。
B. 若$$l \parallel m$$,$$m \subset \alpha$$,则$$l \parallel \alpha$$或$$l \subset \alpha$$,错误。
C. 若$$l \perp m$$,$$m \subset \alpha$$,无法推出$$l \perp \alpha$$,错误。
D. 若$$l \perp \alpha$$,$$m \subset \alpha$$,则$$l \perp m$$,正确。
选D。
6. 由于$$P$$在重心$$G$$的投影,且$$a < b < c$$,锐二面角的大小关系与边长成反比,即$$\alpha > \beta > \gamma$$,选A。
7. 分析各命题:
① 若$$\alpha \parallel \beta$$,且$$m \perp \alpha$$,则$$m \perp \beta$$,又$$n \subset \beta$$,故$$m \perp n$$,正确。
② 若$$\alpha \perp \beta$$,且$$m \perp \alpha$$,$$n \subset \beta$$,$$m$$与$$n$$不一定平行,错误。
③ 若$$m \perp n$$,且$$m \perp \alpha$$,$$n \subset \beta$$,无法推出$$\alpha \perp \beta$$,错误。
④ 若$$m \parallel n$$,且$$m \perp \alpha$$,则$$n \perp \alpha$$,又$$n \subset \beta$$,故$$\alpha \perp \beta$$,正确。
正确的有①和④,选B。
8. 分析各选项:
A. 若$$m \subset \alpha$$,$$n \parallel \alpha$$,则$$m \parallel n$$或异面,错误。
B. 若$$m \perp n$$,$$m \perp \beta$$,则$$n \parallel \beta$$或$$n \subset \beta$$,错误。
C. 若$$\alpha \cap \beta = n$$,$$m \parallel n$$,则$$m \parallel \alpha$$或$$m \parallel \beta$$,但不一定同时成立,错误。
D. 若$$m \perp \alpha$$,$$m \perp \beta$$,则$$\alpha \parallel \beta$$,正确。
选D。
9. 分析各选项:
A. 若$$m \perp \alpha$$,$$n \perp \beta$$,$$\alpha \parallel \beta$$,则$$m \parallel n$$,正确。
B. 若$$m \perp \alpha$$,$$n \parallel \alpha$$,则$$m \perp n$$,正确。
C. 若$$m \parallel n$$,$$n \perp \alpha$$,则$$m \perp \alpha$$,正确。
D. 若$$m \parallel \alpha$$,$$n \subset \alpha$$,$$m \perp n$$,无法推出$$m \perp \alpha$$,错误。
选D。
10. 分析各选项:
A. 若$$l \parallel \alpha$$,$$l \parallel \beta$$,则$$\alpha \parallel \beta$$或相交,错误。
B. 若$$l \perp m$$,$$l \perp n$$,则$$m$$与$$n$$可能平行、相交或异面,错误。
C. 若$$l \parallel m$$,$$l \perp \alpha$$,则$$m \perp \alpha$$,正确。
D. 若$$l$$、$$m$$与$$\alpha$$所成的角相等,则$$l \parallel m$$或相交或异面,错误。
选C。
.jpg)