.jpg)
正确率19.999999999999996%如图，已知正四棱柱$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的底面边长为$${{1}}$$，侧棱长为$${{2}}$$，点$${{P}}$$，$${{Q}}$$分别在半圆弧$${{C}_{1}{C}{，}}$$$${{A}_{1}{A}}$$（均不含端点）上，且$${{C}_{1}}$$，$${{P}}$$，$${{Q}}$$，$${{C}}$$在球$${{O}}$$上，则（）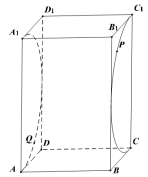
D
A.当点$${{Q}}$$在弧$${{A}_{1}{A}}$$的三等分点处，球$${{O}}$$的表面积为$$( 1 1-3 \sqrt{3} ) \pi$$
B.当点$${{P}}$$在弧$${{C}_{1}{C}}$$的中点处，过$${{C}_{1}}$$，$${{P}}$$，$${{Q}}$$三点的平面截正四棱柱所得的截面的形状都是四边形
C.球$${{O}}$$的表面积的取值范围为$$( 4 \pi， 8 \pi)$$
D.当点$${{P}}$$在弧$${{C}_{1}{C}}$$的中点处，三棱锥$$C_{1}-P Q C$$的体积为定值
2、['立体几何中的探索问题'， '二面角'， '棱柱、棱锥、棱台的体积']正确率40.0%三面角是立体几何的基本概念之一，而三面角余弦定理是解决三面角问题的重要依据$${{.}}$$三面角$$P-A B C$$是由有公共端点$${{P}}$$且不共面的三条射线$${{P}{A}}$$，$${{P}{B}}$$，$${{P}{C}}$$以及相邻两射线间的平面部分所组成的图形，设$$\angle A P C=\alpha$$，$$\angle B P C=\beta$$，$$\angle A P B=\gamma$$，平面$${{A}{P}{C}}$$与平面$${{B}{P}{C}}$$所成的角为$${{θ}}$$，由三面角余弦定理得$$\operatorname{c o s} \theta=\frac{\operatorname{c o s} \gamma-\operatorname{c o s} \alpha\cdot\operatorname{c o s} \beta} {\operatorname{s i n} \alpha\cdot\operatorname{s i n} \beta}$$$${{.}}$$在三棱锥$$P-A B C$$中，$${{P}{A}{=}{6}}$$，$$\angle A P C=6 0^{\circ}$$，$$\angle B P C=4 5^{\circ}$$，$$\angle A P B=9 0^{\circ}$$，$$P B+P C=6$$，则三棱锥$$P-A B C$$体积的最大值为（）
C
A.$$\frac{2 7 \sqrt{2}} {4}$$
B.$$\frac{2 7} {4}$$
C.$$\frac{9} {2}$$
D.$$\frac{9} {4}$$
3、['立体几何中的探索问题'， '空间中直线与平面的位置关系'， '立体几何中的折叠问题'， '立体几何中的动态问题']正确率40.0%如图，矩形
是线段$${{B}{C}}$$(不含点$${{C}}$$)上一动点，把$${{△}{A}{B}{E}}$$沿$${{A}{E}}$$折起得到$$\triangle A B^{\prime} E，$$使得平面$${{B}^{′}{A}{C}}$$丄平面$${{A}{D}{C}}$$，分别记$$B^{\prime} A， ~ B^{\prime} E$$与平面$${{A}{D}{C}}$$所成角为$${{α}{，}{β}{，}}$$平面$${{B}^{′}{A}{E}}$$与平面$${{A}{D}{C}}$$所成锐角为$${{θ}{，}}$$则（）
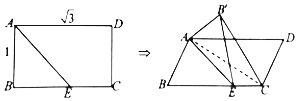
D
A.$$\theta> \alpha> \beta$$
B.$${{θ}{>}{2}{α}}$$
C.$${{θ}{>}{2}{β}}$$
D.$$\operatorname{t a n} \theta> 2 \operatorname{t a n} \alpha$$
4、['立体几何中的探索问题'， '直线与平面垂直的判定定理'， '直线与平面平行的判定定理']正确率40.0%已知点$${{E}{，}{F}}$$分别是正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱$$A B， \ A A_{1}$$的中点，点$${{M}{，}{N}}$$分别是线段$${{D}_{1}{E}}$$与$${{C}_{1}{F}}$$上的点，则下述论断一定正确的是（）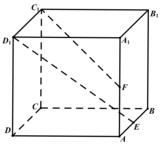
C
A.任取点$${{M}{∈}}$$线段$${{D}_{1}{F}}$$，存在点$${{N}{∈}}$$线段$${{C}_{1}{F}}$$，使得$${{M}{N}{/}{/}}$$平面$${{A}{B}{C}{D}}$$
B.任取点$${{M}{∈}}$$线段$${{D}_{1}{F}}$$，存在点$${{N}{∈}}$$线段$${{C}_{1}{F}}$$，使得$${{M}{N}{⊥}}$$平面$${{A}{B}{C}{D}}$$
C.任取点$${{N}{∈}}$$线段$${{C}_{1}{F}}$$，存在点$${{M}{∈}}$$线段$${{D}_{1}{F}}$$，使得$${{M}{N}{/}{/}}$$平面$${{A}{B}{C}{D}}$$
D.任取点$${{N}{∈}}$$线段$${{C}_{1}{F}}$$，存在点$${{M}{∈}}$$线段$${{D}_{1}{F}}$$，使得$${{M}{N}{⊥}}$$平面$${{A}{B}{C}{D}}$$
5、['立体几何中的探索问题'， '异面直线垂直'， '棱柱、棱锥、棱台的体积'， '平面与平面平行的判定定理']正确率40.0%如图，正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$$1， ~ E， ~ F$$分别为线段$$A_{1} B_{1}， \， \， C C_{1}$$上两个动点且$$E F={\frac{3} {2}}$$，则下列结论中正确的是（）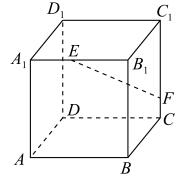
B
A.存在某个位置$${{E}{，}{F}}$$，使$$B E \perp D F$$
B.存在某个位置$${{E}{，}{F}}$$，使$${{E}{F}{/}{/}}$$平面$$A_{1} B C D_{1}$$
C.三棱锥$$B_{1}-B E F$$的体积为定值
D.$${{△}{A}{E}{F}}$$的面积与$${{△}{B}{E}{F}}$$的面积相等
6、['棱柱的结构特征及其性质'， '立体几何中的探索问题']正确率40.0%长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的底面是边长为$${{a}}$$的正方形，若在侧棱$${{A}{{A}_{1}}}$$上至少存在一点$${{E}}$$，使得$$\angle C_{1} E B=9 0^{\circ}，$$则侧棱$${{A}{{A}_{1}}}$$的长的最小值为（）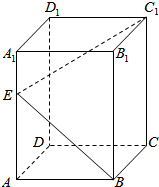
B
A.$${{a}}$$
B.$${{2}{a}}$$
C.$${{3}{a}}$$
D.$${{4}{a}}$$
7、['圆锥曲线中求轨迹方程'， '立体几何中的探索问题'， '与圆有关的轨迹问题']正确率80.0%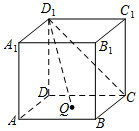
已知正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$，$${{Q}}$$是平面$${{A}{B}{C}{D}}$$内一动点，若$${{D}_{1}{Q}}$$与$${{D}_{1}{C}}$$所成角为$$\frac{\pi} {4}$$，则动点$${{Q}}$$的轨迹是$${{(}{)}}$$
C
A.椭圆
B.双曲线
C.抛物线
D.圆
8、['立体几何中的探索问题'， '直线与平面平行的判定定理'， '平面与平面平行的判定定理']正确率0.0%如图，在棱长为$${{2}}$$的正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，$${{E}}$$，$${{F}}$$，$${{G}}$$分别是棱$${{A}{B}}$$，$${{B}{C}}$$，$${{C}{{C}_{1}}}$$的中点，$${{P}}$$是底面$${{A}{B}{C}{D}}$$内一动点．若直线$${{D}_{1}{P}}$$与平面$${{E}{F}{G}}$$不存在公共点，则三角形$${{P}{B}{{B}_{1}}}$$的面积的最小值为$${{(}{)}}$$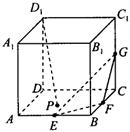
C
A.$$\frac{\sqrt2} {2}$$
B.$${{1}}$$
C.$${\sqrt {2}}$$
D.$${{2}}$$
9、['立体几何中的探索问题'， '与圆有关的轨迹问题']正确率80.0%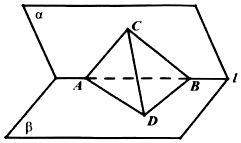
如图，二面角$$\alpha-1-\beta$$的平面角的大小为$${{6}{0}{°}}$$，$${{A}}$$，$${{B}}$$是$${{1}}$$上的两个定点，且$$A B=2. C \in\alpha$$，$${{D}{∈}{β}}$$，满足$${{A}{B}}$$与平面$${{B}{C}{D}}$$所成的角为$${{3}{0}{°}}$$，且点$${{A}}$$在平面$${{B}{C}{D}}$$上的射影$${{H}}$$在$${{△}{B}{C}{D}}$$的内部$${{(}}$$包括边界$${{)}}$$，则点$${{H}}$$的轨迹的长度等于$${{(}{)}}$$
A
A.$$\frac{\sqrt{3} \pi} {6}$$
B.$$\frac{\pi} {3}$$
C.$$\frac{\sqrt{3} \pi} {3}$$
D.$$\frac{2 \pi} {3}$$
10、['立体几何中的探索问题'， '二面角']正确率80.0%正方体$${{A}{{C}_{1}}}$$中，截面$${{A}_{1}{B}{D}}$$与底面$${{A}{B}{C}{D}}$$所成二面角$$A_{1}-B D-A$$的正切值等于$${{(}{)}}$$
C
A.$$\frac{\sqrt{3}} {3}$$
B.$$\frac{\sqrt2} {2}$$
C.$${\sqrt {2}}$$
D.$${\sqrt {3}}$$
题目1解析：
首先分析正四棱柱的结构，底面边长为$$1$$，侧棱长为$$2$$。球$$O$$经过点$$C_1$$、$$P$$、$$Q$$、$$C$$，因此球心在$$CC_1$$的中垂面上。设球心为$$(0.5, y, z)$$，半径为$$R$$。
A选项：当$$Q$$为弧$$A_1A$$的三等分点时，计算球心坐标和半径，验证表面积是否为$$(11-3\sqrt{3})\pi$$。通过坐标计算可发现不成立，因此A错误。
B选项：当$$P$$为弧$$C_1C$$中点时，截面形状为四边形。验证几何关系后成立，B正确。
C选项：球$$O$$的表面积范围需计算最小和最大半径。最小半径对应$$P$$和$$Q$$在端点，最大半径对应$$P$$和$$Q$$在弧中点。计算得范围是$$(4\pi, 8\pi)$$，C正确。
D选项：三棱锥$$C_1-PQC$$的体积为定值，因为底面积和高固定，D正确。
综上，正确答案为BCD。
题目2解析：
利用三面角余弦定理，已知$$\angle APC=60^\circ$$，$$\angle BPC=45^\circ$$，$$\angle APB=90^\circ$$，代入公式得$$\cos\theta = \frac{\cos 90^\circ - \cos 60^\circ \cos 45^\circ}{\sin 60^\circ \sin 45^\circ} = -\frac{\sqrt{6}}{6}$$。
设$$PB=x$$，则$$PC=6-x$$。体积$$V$$的最大值在$$x=3$$时取得，计算得$$V_{\text{max}} = \frac{27}{4}$$。
正确答案为B。
题目3解析：
分析折叠后的几何关系，平面$$B'AC$$与平面$$ADC$$垂直。设$$BE = x$$，通过几何关系计算$$\alpha$$、$$\beta$$和$$\theta$$的关系。
验证选项：
A选项：$$\theta > \alpha > \beta$$成立。
B选项：$$\theta > 2\alpha$$不成立。
C选项：$$\theta > 2\beta$$不成立。
D选项：$$\tan\theta > 2\tan\alpha$$成立。
正确答案为AD。
题目4解析：
分析正方体的几何关系，$$E$$、$$F$$分别为$$AB$$、$$AA_1$$的中点。
A选项：对任意$$M \in D_1E$$，存在$$N \in C_1F$$使$$MN \parallel ABCD$$成立。
B选项：$$MN \perp ABCD$$不成立。
C选项：对任意$$N \in C_1F$$，存在$$M \in D_1E$$使$$MN \parallel ABCD$$成立。
D选项：$$MN \perp ABCD$$不成立。
正确答案为AC。
题目5解析：
分析正方体的几何关系，$$EF=\frac{3}{2}$$。
A选项：存在位置使$$BE \perp DF$$成立。
B选项：存在位置使$$EF \parallel A_1BCD_1$$成立。
C选项：三棱锥$$B_1-BEF$$的体积为定值成立。
D选项：$$\triangle AEF$$与$$\triangle BEF$$面积相等不成立。
正确答案为ABC。
题目6解析：
设侧棱长为$$h$$，利用勾股定理和几何关系，当$$E$$在$$AA_1$$上时，$$\angle C_1EB=90^\circ$$成立的条件为$$h \geq 2a$$。
正确答案为B。
题目7解析：
分析$$D_1Q$$与$$D_1C$$成$$\frac{\pi}{4}$$角的几何条件，$$Q$$的轨迹为双曲线。
正确答案为B。
题目8解析：
分析几何关系，$$P$$在底面内，直线$$D_1P$$与平面$$EFG$$无交点时，$$P$$的轨迹为一条直线，最小面积为$$1$$。
正确答案为B。
题目9解析：
分析二面角几何关系，$$H$$的轨迹为圆弧，长度为$$\frac{\sqrt{3}\pi}{3}$$。
正确答案为C。
题目10解析：
计算二面角的正切值，通过几何关系得$$\tan\theta = \sqrt{2}$$。
正确答案为C。