正确率19.999999999999996%$${{A}{B}{C}{D}}$$是球$${{O}}$$内接正四面体,若球$${{O}}$$的半径为$${{1}}$$,则$$( \overrightarrow{O A}+\overrightarrow{O B} ) \cdot( \overrightarrow{O C}+\overrightarrow{O D} )=~ ($$)
B
A.$$\frac{4} {3}$$
B.$$- \frac{4} {3}$$
C.$$\frac{1} {3}$$
D.$$- \frac{1} {3}$$
2、['立体几何中的四点共面、三点共线']正确率40.0%已知$$M, ~ A, ~ B, ~ C$$是空间任意四点,其中$$A, ~ B, ~ C$$三点不共线,对平面$${{A}{B}{C}}$$外的任一点$${{O}{,}}$$下列条件中不能确定点$$M, ~ A, ~ B, ~ C$$共面的是()
C
A.$$\overrightarrow{O M}=\overrightarrow{O A}+\overrightarrow{O B}-\overrightarrow{O C}$$
B.$$\overrightarrow{O M}=\frac{1} {3} \overrightarrow{O A}+\frac{1} {3} \overrightarrow{O B}+\frac{1} {3} \overrightarrow{O C}$$
C.$$\overrightarrow{O M}=\overrightarrow{O A}+\frac{1} {2} \overrightarrow{O B}+\frac{1} {4} \overrightarrow{O C}$$
D.$$\overrightarrow{O M}=3 \overrightarrow{O A}-\overrightarrow{O B}-\overrightarrow{O C}$$
3、['立体几何中的四点共面、三点共线']正确率60.0%已知$$A, ~ B, ~ C$$三点不共线,对平面$${{A}{B}{C}}$$外的任意一点$${{O}{,}}$$下列条件中能确定点$$M, ~ A, ~ B, ~ C$$共面的是()
D
A.$$\overrightarrow{O M}=\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}$$
B.$$\overrightarrow{O M}=2 \overrightarrow{O A}-\overrightarrow{O B}-\overrightarrow{O C}$$
C.$$\overrightarrow{O M}=\overrightarrow{O A}+\frac{1} {2} \overrightarrow{O B}+\frac{1} {3} \overrightarrow{O C}$$
D.$$\overrightarrow{O M}=\frac{1} {3} \overrightarrow{O A}+\frac{1} {3} \overrightarrow{O B}+\frac{1} {3} \overrightarrow{O C}$$
4、['立体几何中的四点共面、三点共线', '空间四边形', '基本事实1', '基本事实的推论']正确率60.0%下列命题中正确的个数有()
$${{(}{1}{)}}$$三条平行线最多可以确定$${{3}}$$个平面;
$${{(}{2}{)}}$$四条边都相等的四边形一定是菱形;
$${{(}{3}{)}}$$三条直线相交于一点,可以确定$${{1}}$$个或$${{3}}$$个平面;
$${{(}{4}{)}}$$若点$${{P}}$$不在平面$${{α}}$$内,点$$A. ~ B. ~ C$$三点均在$${{α}}$$内,则$$P_{\smallsetminus} \ A_{\smallsetminus} \ B_{\nsim} \ C$$四点一定不共面.
B
A.$${{1}}$$个
B.$${{2}}$$个
C.$${{3}}$$个
D.$${{4}}$$个
5、['立体几何中的四点共面、三点共线', '基本事实3', '基本事实2', '基本事实1']正确率60.0%在空间给出下列命题(设$${{α}{、}{β}}$$表示平面,$${{l}}$$表示直线,$$A, ~ B, ~ C$$表示点)其中真命题有()
$${({1}{)}}$$若$$A \in l, \, \, \, A \in\alpha, \, \, \, B \in\alpha, \, \, \, B \in l$$,则$${{l}{⊂}{α}}$$
$${\bf( 2 )} \, \, \, A \in\alpha, \, \, \, A \in\beta, \, \, \, B \in\alpha, \, \, \, B \in\beta$$,则$$\alpha\cap\beta=A B$$
$${({3}{)}}$$若$$l \not\subset\alpha, \, \, A \in l$$,则$${{A}{∉}{α}}$$
$${({4}{)}}$$若$$A, ~ B, ~ C \in\alpha, ~ ~ A, ~ ~ B, ~ C \in\beta$$,且$$A. ~ B. ~ C$$不共线,则$${{α}}$$与$${{β}}$$重合.
C
A.$${{1}}$$个
B.$${{2}}$$个
C.$${{3}}$$个
D.$${{4}}$$个
6、['立体几何中的四点共面、三点共线', '空间向量基本定理的应用']正确率60.0%在正方体中$$A B C D-A_{1} B_{1} C_{1} D_{1}$$,若$${{G}}$$点是$${{△}{B}{{A}_{1}}{D}}$$的重心,且$$\overrightarrow{A G}=x \overrightarrow{A D}+y \overrightarrow{A B}+z \overrightarrow{C C_{1}},$$则$$x+y+z$$的值为()
B
A.$${{3}}$$
B.$${{1}}$$
C.$${{−}{1}}$$
D.$${{−}{3}}$$
7、['立体几何中的四点共面、三点共线', '基本事实的推论']正确率60.0%如图所示$$, P, ~ Q, ~ R, ~ S$$分别是所在棱的中点,则这四个点不共面的是()
D
A.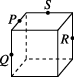
B.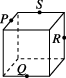
C.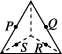
D.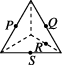
正确率40.0%如图,长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$$A B=1 6, \, \, B C=1 0, \, \, \, A a_{1}=8$$,点$${{E}{,}{F}}$$分别在$$A_{1} B_{1}, ~ D_{1} C_{1}$$上,$$A_{1} E=D_{1} F=4$$,过点$${{E}{,}{F}}$$的平面$${{α}}$$与此长方体的面相交,交线围成一个正方形$${{E}{F}{G}{B}}$$.则$${{H}{B}{=}}$$()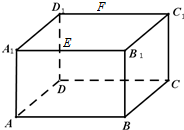
A
A.$${{6}}$$
B.$${{7}}$$
C.$${{8}}$$
D.$${{9}}$$
9、['立体几何中的四点共面、三点共线', '立体几何中的截面、交线问题', '命题的真假性判断']正确率60.0%在空间中,下列结论正确的是$${{(}{)}}$$
D
A.空间三点确定一个平面
B.空间四点确定一个平面
C.直线和空间一点确定一个平面
D.过空间四点最多有四个平面
10、['立体几何中的四点共面、三点共线', '共面向量定理', '空间向量基本定理的应用']正确率60.0%对于空间任意一点$${{O}}$$和不共线的三点$$A, B, C$$,有如下关系:$$6 \overrightarrow{O P}=\overrightarrow{O A}+2 \overrightarrow{O B}+3 \overrightarrow{O C}$$,则()
B
A.四点$${{O}}$$,$${{A}}$$,$${{B}{,}{C}}$$必共面
B.四点$${{P}}$$,$${{A}}$$,$${{B}{,}{C}}$$必共面
C.四点$${{O}}$$,$$P, ~ B, ~ C$$必共面
D.五点$${{O}}$$,$${{P}}$$,$${{A}}$$,$${{B}{,}{C}}$$必共面
1. 解析:
2. 解析:
3. 解析:
4. 解析:
5. 解析:
6. 解析:
7. 解析:
8. 解析:
9. 解析:
10. 解析:
.jpg)