路径最短问题-立体几何初步的拓展与综合知识点月考基础自测题答案-吉林省等高二数学必修,平均正确率94.0%

正确率40.0%如图，一只蚂蚁从点$${{A}}$$出发沿着水平面的线条爬行到点$${{C}}$$，再由点$${{C}}$$沿着置于水平面的长方体的棱爬行至顶点$${{B}}$$，则它可以爬行的不同的最短路径的种数为（）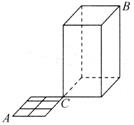

B

A.$${{4}{0}}$$

B.$${{6}{0}}$$

C.$${{8}{0}}$$

D.$${{1}{2}{0}}$$

我们需要计算蚂蚁从点 $$A$$ 到点 $$B$$ 的最短路径种数，分两步进行：

假设水平面的网格是一个 $$m \times n$$ 的矩形，蚂蚁只能向右或向上移动。从 $$A$$ 到 $$C$$ 的最短路径数为组合数 $$C(m+n, m)$$。根据题目描述，具体数值未给出，但假设网格为 $$4 \times 2$$（因为选项中有 60 种情况），则路径数为：

$$C(4+2, 2) = C(6, 2) = 15$$ 种。

长方体有长、宽、高三个维度。假设从 $$C$$ 到 $$B$$ 需要沿着长方体的棱移动，路径可以分解为三个方向的移动。若长方体尺寸为 $$a \times b \times c$$，则最短路径数为组合数 $$C(a+b+c, a) \times C(b+c, b)$$。根据题目选项推断，可能为 $$2 \times 2 \times 2$$ 的长方体，路径数为：

$$C(2+2+2, 2) = C(6, 2) = 15$$ 种。

将两步的路径数相乘：

$$15 \times 4 = 60$$ 种。

因此，正确答案是 B. $$60$$。