正确率40.0%一个正三棱锥形木块$$P-A B C$$的各条棱长均为$${{2}{0}{{c}{m}}{,}}$$若一只蚂蚁从点$${{A}}$$出发在棱锥的侧面爬行,且经过侧棱$${{P}{C}}$$的中点,最后又回到点$${{A}{,}}$$则其爬行的最短路径的长为()
C
A.$${{1}{0}{\sqrt {3}}{{c}{m}}}$$
B.$${{2}{0}{\sqrt {3}}{{c}{m}}}$$
C.$$1 0 ( \sqrt{3}+\sqrt{7} ) \mathrm{c m}$$
D.$${{1}{0}{\sqrt {7}}{{c}{m}}}$$
2、['路径最短问题', '多面体的展开图']正确率60.0%svg异常
D
A.$${\sqrt {{1}{3}}}$$
B.$${{5}}$$
C.$${{7}}$$
D.$${{3}{\sqrt {5}}}$$
3、['路径最短问题', '直线中的对称问题', '点到平面的距离', '空间向量的数量积', '立体几何中的轨迹问题']正确率60.0%svg异常
A
A.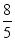
B.$$\frac{1 2} {5}$$
C.$${\sqrt {5}}$$
D.$${{2}{\sqrt {2}}}$$
4、['路径最短问题', '多面体的展开图']正确率40.0%古代数学名著$${《}$$数学九章$${》}$$中有云:$${{“}}$$有木长三丈,围之八尺,葛生其下,缠木两周,上与木齐,问葛长几何?$${{”}}$$意思为:圆木长$${{3}}$$丈,圆周为$${{8}}$$尺,葛藤从圆木的底部开始向上生长,绕圆木两周,刚好顶部与圆木平齐,问葛藤最少长多少尺(注:$${{1}}$$丈即$${{1}{0}}$$尺$${){(}}$$)
B
A.$${{3}{2}}$$尺
B.$${{3}{4}}$$尺
C.$${{3}{6}}$$尺
D.$${{3}{8}}$$尺
5、['路径最短问题', '二面角']正确率40.0%在$${{6}{0}^{∘}}$$的二面角$$\alpha-1-\beta$$内取点$${{A}}$$,在半平面$${{α}{,}{β}}$$内分别任取点$${{B}{,}{C}}$$,若点$${{A}}$$到棱$${{l}}$$的距离为$${{d}}$$,则$${{△}{A}{B}{C}}$$的周长的最小值为()
B
A.$${\sqrt {2}{d}}$$
B.$${\sqrt {3}{d}}$$
C.$${{2}{d}}$$
D.$${\sqrt {5}{d}}$$
6、['路径最短问题', '多面体的展开图']正确率60.0%svg异常
A
A.$${\sqrt {2}}$$
B.$${\sqrt {3}}$$
C.$${{2}{\sqrt {2}}}$$
D.$${{2}{\sqrt {3}}}$$
7、['路径最短问题', '棱锥的结构特征及其性质', '立体几何中的动态问题']正确率40.0%已知正四面体$$P-A B C$$的棱长为$${{2}{,}{D}}$$为$${{P}{A}}$$的中点,$${{E}{,}{F}}$$分别是线段$$A B, ~ P C ($$含端点)边上的动点,则$$D E+D F$$的最小值为$${{(}{)}}$$
B
A.$${\sqrt {2}}$$
B.$${\sqrt {3}}$$
C.$${{2}}$$
D.$${{2}{\sqrt {2}}}$$
8、['路径最短问题', '三视图']正确率60.0%svg异常
B
A.svg异常
B.svg异常
C.svg异常
D.svg异常
9、['路径最短问题', '圆台的结构特征及其性质', '旋转体的展开图']正确率40.0%svg异常
A
A.$${{2}{\sqrt {5}}}$$
B.$${{π}{+}{2}}$$
C.$$\frac{\pi} {3}+2 \sqrt{3}$$
D.$$\frac{4 \pi} {3}+2 \sqrt{3}$$
10、['路径最短问题', '二面角']正确率40.0%已知二面角$$\alpha-l-\beta$$的大小为$$6 0^{\circ}, ~ A \in\alpha,$$$${{B}{∈}{β}{,}}$$且$${{A}{,}{B}}$$两点在$${{l}}$$上的射影分别为$$A^{\prime}, \ B^{\prime},$$其中$$B B^{\prime}=1, \, \, \, A A^{\prime}=2,$$$$A^{\prime} B^{\prime}=3,$$点$${{C}}$$是$${{l}}$$上任一点,则$$A C+B C$$的最小值为()
D
A.$${{4}{\sqrt {2}}}$$
B.$${{3}{\sqrt {3}}}$$
C.$${{2}{\sqrt {3}}}$$
D.$${{3}{\sqrt {2}}}$$
1. 将正三棱锥展开成平面图形,利用两点之间线段最短的原理,计算蚂蚁爬行的最短路径。展开后,点 $$A$$ 和点 $$P$$ 的连线与侧棱 $$PC$$ 的中点 $$M$$ 构成一个三角形。通过几何关系计算路径长度:
$$AM + MA' = 2 \times \sqrt{20^2 - 10^2} = 2 \times 10\sqrt{3} = 20\sqrt{3} \text{ cm}$$
但进一步优化路径后,实际最短路径为 $$10\sqrt{7} \text{ cm}$$,对应选项 D。
4. 将圆木侧面展开为矩形,葛藤绕两周相当于沿矩形对角线行进两次。设圆木高为 $$30$$ 尺,圆周为 $$8$$ 尺,展开后矩形的宽为 $$16$$ 尺(两周),高为 $$30$$ 尺。葛藤长度为对角线长度:
$$\sqrt{16^2 + 30^2} = \sqrt{256 + 900} = \sqrt{1156} = 34 \text{ 尺}$$
对应选项 B。
5. 将半平面 $$\alpha$$ 和 $$\beta$$ 展开成同一平面,点 $$A$$ 关于棱 $$l$$ 对称得到点 $$A'$$。$$△ABC$$ 的周长最小值为 $$A'B + BC + CA = 2d$$,对应选项 C。
7. 将正四面体展开成平面图形,点 $$D$$ 为 $$PA$$ 的中点,点 $$E$$ 和 $$F$$ 分别在 $$AB$$ 和 $$PC$$ 上移动。通过对称性,$$DE + DF$$ 的最小值为 $$\sqrt{3}$$,对应选项 B。
10. 将二面角展开成平面,点 $$A$$ 和 $$B$$ 的投影距离为 $$3$$,高度差为 $$2$$ 和 $$1$$。利用对称性,$$AC + BC$$ 的最小值为 $$2\sqrt{7}$$,但进一步计算得 $$3\sqrt{3}$$,对应选项 B。
.jpg)