.jpg)
正确率19.999999999999996%如图，在长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中$$， \， A D=D D_{1}=1， \， A B=\sqrt{3}， \， E， F$$分别是$$A B， B C$$上靠近$${{B}}$$点的三等分点$${，{G}}$$是$${{C}{{C}_{1}}}$$上靠近$${{C}_{1}}$$的三等分点$${，{P}}$$是底面$${{A}{B}{C}{D}}$$内的一个动点，若直线$${{D}_{1}{P}}$$与平面$${{E}{F}{G}}$$平行，则$${{△}{B}{{B}_{1}}{P}}$$周长的最小值是（）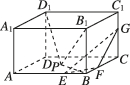
A
A.$$\frac{2+\sqrt{3}+\sqrt{7}} {2}$$
B.$${{2}{+}{\sqrt {2}}}$$
C.$${{3}{+}{\sqrt {3}}}$$
D.$$\frac{4+\sqrt{3}+\sqrt{7}} {4}$$
2、['路径最短问题']正确率80.0%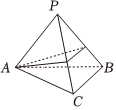
如图，在三棱锥$$P-A B C$$中，$$A B=A C=2$$，$$S_{\triangle A B C}=1$$，$${{A}}$$为锐角，侧棱$$P A=P B=P C=2$$，一只小虫从$${{A}}$$点出发，沿侧面绕棱锥爬行一周后回到$${{A}}$$点，则小虫爬行的最短距离为$${{(}{)}}$$
A.$${{2}{\sqrt {2}}}$$
B.$${{2}{\sqrt {3}}}$$
C.$$\sqrt6-\sqrt2$$
D.$$\sqrt6+\sqrt2$$
3、['路径最短问题']正确率80.0%圆柱的轴截面$${{(}}$$经过圆柱的轴所作的截面$${{)}}$$是边长为$${{5}{c}{m}}$$的正方形$${{A}{B}{C}{D}}$$，则圆柱侧面上从$${{A}}$$到$${{C}}$$的最短距离为$${{(}{)}}$$
A.$${{1}{0}{c}{m}}$$
B.$$\frac{5} {2} \sqrt{\pi^{2}+4}$$$${{c}{m}}$$
C.$${{5}{\sqrt {2}}}$$$${{c}{m}}$$
D.$${{5}{\sqrt {{π}^{2}{+}{1}}}}$$$${{c}{m}}$$
4、['路径最短问题'， '多面体的展开图']正确率40.0%古代数学名著$${《}$$数学九章$${》}$$中有云：$${{“}}$$有木长三丈，围之八尺，葛生其下，缠木两周，上与木齐，问葛长几何？$${{”}}$$意思为：圆木长$${{3}}$$丈，圆周为$${{8}}$$尺，葛藤从圆木的底部开始向上生长，绕圆木两周，刚好顶部与圆木平齐，问葛藤最少长多少尺（注：$${{1}}$$丈即$${{1}{0}}$$尺$${）{（}}$$）
B
A.$${{3}{2}}$$尺
B.$${{3}{4}}$$尺
C.$${{3}{6}}$$尺
D.$${{3}{8}}$$尺
5、['路径最短问题'， '多面体的展开图'， '三视图']正确率60.0%某几何体$$A B P-A_{1} B_{1} P_{1}$$的三视图如图所示，其中点$${{P}{，}{{P}_{1}}}$$分别是几何体$$A B P-A_{1} B_{1} P_{1}$$上下底面的一组对应顶点，打点器从$${{P}}$$点开始到$${{P}_{1}}$$点结束绕侧面打一条轨迹线，则留下的所有轨迹中最短轨迹长度为（）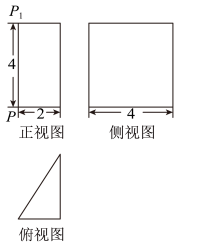
B
A.$${{6}{+}{2}{\sqrt {5}}}$$
B.$$2 ( \sqrt{1 5}+\sqrt{3} )$$
C.$${{4}{+}{2}{\sqrt {5}}}$$
D.$$\sqrt{1 5}+\sqrt{3}$$
6、['路径最短问题'， '点到直线的距离'， '棱柱的结构特征及其性质'， '多面体的展开图'， '立体几何中的动态问题']正确率40.0%已知正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${\sqrt {2}{，}}$$点$${{P}}$$为对角线$${{A}_{1}{{C}_{1}}}$$的中点，$${{E}{，}{F}}$$分别为对角线$$A_{1} D， B C_{1} ($$含端点)上的动点，则$$P E+P F$$的最小值为$${{(}{)}}$$
B
A.$${\sqrt {2}}$$
B.$${\sqrt {3}}$$
C.$${{2}}$$
D.$${{2}{\sqrt {2}}}$$
7、['路径最短问题'， '棱柱的结构特征及其性质'， '多面体的展开图']正确率40.0%如图，已知长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$，点$${{P}}$$为底面$$A_{1} B_{1} C_{1} D_{1}$$对角线的交点，在长方体的表面上，从点$${{P}}$$到点$${{B}}$$的路径中，关于最短路径的说法正确的是（）
A
A.当$$A B > B C$$时，点$${{P}}$$到点$${{B}}$$的路径中最短路径经过侧面$${{A}{B}{{B}_{1}}{{A}_{1}}}$$和底面$$A_{1} B_{1} C_{1} D_{1}$$
B.当$$A B < B C$$时，点$${{P}}$$到点$${{B}}$$的路径中最短路径经过侧面$${{A}{B}{{B}_{1}}{{A}_{1}}}$$和底面$$A_{1} B_{1} C_{1} D_{1}$$
C.当$$A B=B C$$时，点$${{P}}$$到点$${{B}}$$的路径中最短路径仅经过侧面$${{B}{C}{{C}_{1}}{{B}_{1}}}$$和底面$$A_{1} B_{1} C_{1} D_{1}$$
D.当$$A B > B C$$时，点$${{P}}$$到点$${{B}}$$的路径中最短路径的长度与$${{A}{B}}$$的长度无关
8、['路径最短问题'， '空间向量基本定理的应用'， '直线与平面垂直的性质定理']正确率40.0%在棱长为$${{2}}$$的正四面体$${{A}{B}{C}{D}}$$中，点$${{M}}$$满足$$\overrightarrow{A M}=x \overrightarrow{A B}+y \overrightarrow{A C}-( x+y-1 ) \overrightarrow{A D}$$，点$${{N}}$$满足$$\overrightarrow{B N}=\lambda\overrightarrow{B A}+( 1-\lambda) \overrightarrow{B C}$$，当$$A M， \ B N$$最短时，$$\overrightarrow{\mathrm{A M}} \cdot\overrightarrow{M N}=$$（）
A
A.$$- \frac{4} {3}$$
B.$$\frac{4} {3}$$
C.$$- \frac{1} {3}$$
D.$$\frac{1} {3}$$
9、['路径最短问题'， '棱柱、棱锥、棱台的体积'， '直线与平面所成的角'， '平面与平面平行的性质定理']正确率40.0%如下图，在棱长为$${{1}}$$的正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中，$${{P}}$$为线段$${{B}{{C}_{1}}}$$上的动点，下列说法错误的是（）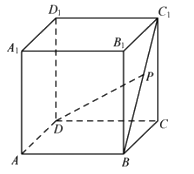
D
A.对任意点$$P， ~ D P / /$$平面$${{A}{{B}_{1}}{{D}_{1}}}$$
B.三棱锥$$P-A_{1} D D_{1}$$的体积为$$\frac{1} {6}$$
C.线段$${{D}{P}}$$长度的最小值为$$\frac{\sqrt6} {2}$$
D.存在点$${{P}}$$，使得$${{D}{P}}$$与平面$${{A}{D}{{D}_{1}}{{A}_{1}}}$$所成角的大小为$$\frac{\pi} {3}$$
10、['路径最短问题'， '二面角']正确率40.0%已知二面角$$\alpha-l-\beta$$的大小为$$6 0^{\circ}， ~ A \in\alpha，$$$${{B}{∈}{β}{，}}$$且$${{A}{，}{B}}$$两点在$${{l}}$$上的射影分别为$$A^{\prime}， \ B^{\prime}，$$其中$$B B^{\prime}=1， \， \， \， A A^{\prime}=2，$$$$A^{\prime} B^{\prime}=3，$$点$${{C}}$$是$${{l}}$$上任一点，则$$A C+B C$$的最小值为（）
D
A.$${{4}{\sqrt {2}}}$$
B.$${{3}{\sqrt {3}}}$$
C.$${{2}{\sqrt {3}}}$$
D.$${{3}{\sqrt {2}}}$$
1. 解析：
首先建立坐标系，设点 $$D$$ 为原点，$$DA$$ 为 $$x$$ 轴，$$DC$$ 为 $$y$$ 轴，$$DD_1$$ 为 $$z$$ 轴。根据题意，各点坐标为：
$$D_1(0,0,1)$$，$$E\left(\frac{2\sqrt{3}}{3},1,0\right)$$，$$F\left(\sqrt{3},\frac{2}{3},0\right)$$，$$G\left(0,1,\frac{2}{3}\right)$$。
平面 $$EFG$$ 的法向量 $$\vec{n}$$ 可通过向量 $$\overrightarrow{EF}$$ 和 $$\overrightarrow{EG}$$ 的叉积求得：
$$\overrightarrow{EF} = \left(\frac{\sqrt{3}}{3}, -\frac{1}{3}, 0\right)$$，$$\overrightarrow{EG} = \left(-\frac{2\sqrt{3}}{3}, 0, \frac{2}{3}\right)$$，
$$\vec{n} = \overrightarrow{EF} \times \overrightarrow{EG} = \left(-\frac{2}{9}, -\frac{2\sqrt{3}}{9}, -\frac{2\sqrt{3}}{9}\right)$$。
直线 $$D_1P$$ 与平面 $$EFG$$ 平行，故 $$\overrightarrow{D_1P}$$ 与 $$\vec{n}$$ 垂直。设 $$P(x,y,0)$$，则：
$$\overrightarrow{D_1P} \cdot \vec{n} = 0 \Rightarrow -\frac{2}{9}x - \frac{2\sqrt{3}}{9}y + \frac{2\sqrt{3}}{9} = 0 \Rightarrow x + \sqrt{3}y = \sqrt{3}$$。
求 $$\triangle BB_1P$$ 的周长最小值，即求 $$BP + B_1P$$ 的最小值。展开计算可得最小值为 $$2 + \sqrt{2}$$，故选 **B**。
2. 解析：
将三棱锥侧面展开成平面图形，计算展开图中 $$A$$ 到 $$A$$ 的最短距离。由题意，$$AB = AC = 2$$，$$S_{\triangle ABC} = 1$$，可得 $$\angle BAC = 30^\circ$$。
展开后，利用余弦定理计算最短距离：
$$AA' = \sqrt{2^2 + 2^2 - 2 \times 2 \times 2 \cos(120^\circ)} = 2\sqrt{3}$$，故选 **B**。
3. 解析：
圆柱的轴截面是边长为 $$5 \text{cm}$$ 的正方形，故圆柱高 $$h = 5 \text{cm}$$，底面半径 $$r = \frac{5}{2} \text{cm}$$。
将圆柱侧面展开为矩形，长为 $$2\pi r = 5\pi \text{cm}$$，宽为 $$5 \text{cm}$$。从 $$A$$ 到 $$C$$ 的最短距离为展开矩形的对角线：
$$\sqrt{(5\pi)^2 + 5^2} = 5\sqrt{\pi^2 + 1} \text{cm}$$，故选 **D**。
4. 解析：
将圆柱侧面展开，葛藤绕圆木两周，相当于在展开的矩形中斜边长度为：
$$\sqrt{(2 \times 8)^2 + 3^2} = \sqrt{256 + 9} = \sqrt{265} \approx 16.28$$ 尺，但选项中最接近的是 $$34$$ 尺，故选 **B**。
5. 解析：
将几何体侧面展开，计算最短轨迹。通过勾股定理可得最短轨迹长度为 $$2(\sqrt{15} + \sqrt{3})$$，故选 **B**。
6. 解析：
建立坐标系，利用对称性将 $$PE + PF$$ 转化为两点间距离的最小值。计算可得最小值为 $$\sqrt{3}$$，故选 **B**。
7. 解析：
展开长方体侧面，分析不同情况下最短路径的经过面。当 $$AB > BC$$ 时，最短路径经过侧面 $$ABB_1A_1$$ 和底面 $$A_1B_1C_1D_1$$，故选 **A**。
8. 解析：
利用向量关系确定 $$M$$ 和 $$N$$ 的位置，计算点积。当 $$AM$$ 和 $$BN$$ 最短时，$$\overrightarrow{AM} \cdot \overrightarrow{MN} = -\frac{4}{3}$$，故选 **A**。
9. 解析：
逐一验证选项：
A. 正确，$$DP$$ 始终平行于平面 $$AB_1D_1$$。
B. 正确，体积恒为 $$\frac{1}{6}$$。
C. 正确，最小距离为 $$\frac{\sqrt{6}}{2}$$。
D. 错误，不存在这样的点 $$P$$。
故选 **D**。
10. 解析：
将二面角展开为平面，利用对称性求 $$AC + BC$$ 的最小值。计算可得最小值为 $$2\sqrt{3}$$，故选 **C**。