正确率40.0%我国魏晋时期的数学家刘徽创造了一个称为“牟合方盖”的立体图形来推算球的体积,如图①,在一个棱长为$${{2}{a}}$$的正方体内作两个互相垂直的内切圆柱,其相交的部分就是“牟合方盖”,如图②,设平行于水平面且与水平面距离为$${{h}}$$的平面为$${{α}{,}}$$记平面$${{α}}$$截“牟合方盖”所得截面的面积为$${{S}{,}}$$则函数$$S=f ( h )$$的大致图像是()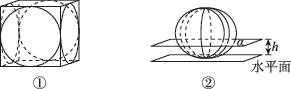
D
A.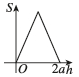
B.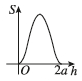
C.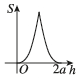
D.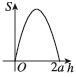
正确率40.0%如图,正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的一个截面经过顶点$${{A}{,}{C}}$$及棱$${{A}_{1}{{B}_{1}}}$$上一点$${{K}{,}}$$截面将正方体分成体积比为$${{2}}$$∶$${{1}}$$的两部分,则$${\frac{A_{1} K} {K B_{1}}}$$的值为()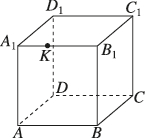
C
A.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
B.$$\frac{{\sqrt5}+1} {2}$$
C.$$\frac{{\sqrt5}-1} {2}$$
D.$$\frac{3-\sqrt{5}} {2}$$
3、['立体几何中的截面、交线问题']正确率60.0%在一个倒置的正三棱锥容器内放入一个钢球,钢球恰与棱锥的四个面都接触,过棱锥的一条侧棱和高作截面,正确的截面图形是()
B
A.
B.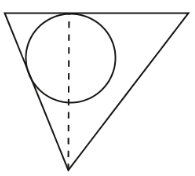
C.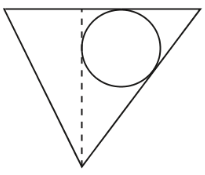
D.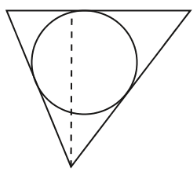
正确率40.0%如图所示,已知正四棱柱(底面为正方形的直棱柱$$\, ) \, \, A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$$B C=1, \, \, \, A A_{1}=\sqrt{2}, \, \, \, a$$为过直线$${{A}{{C}_{1}}}$$且与棱$${{B}{{B}_{1}}}$$相交的平面,则$${{a}}$$截该正四棱柱的截面面积的最小值是()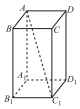
D
A.$$\frac{\sqrt6} {2}$$
B.$$\frac{\sqrt3} {2}$$
C.$${\sqrt {3}}$$
D.$${\sqrt {2}}$$
5、['立体几何中的截面、交线问题', '利用基本不等式求最值', '直线与平面平行的性质定理']正确率19.999999999999996%已知正四面体$${{A}{B}{C}{D}}$$的棱长为$${{2}}$$,平面$${{α}}$$与棱$${{A}{B}}$$、$${{C}{D}}$$均平行,则$${{α}}$$截此正四面体所得截面面积的最大值为()
A
A.$${{1}}$$
B.$${\sqrt {2}}$$
C.$${\sqrt {3}}$$
D.$${{2}}$$
6、['立体几何中的截面、交线问题', '椭圆的离心率']正确率60.0%如图,一个底面半径为$${{R}}$$的圆柱被与其底面所在平面的夹角为$$\theta( 0^{\circ} < \theta< 9 0^{\circ} )$$的平面所截,截面是一个椭圆,当$${{θ}}$$为$${{3}{0}^{∘}}$$时,这个椭圆的离心率为()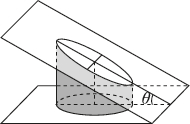
A
A.$$\frac{1} {2}$$
B.$$\frac{\sqrt3} {2}$$
C.$$\frac{1} {3}$$
D.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
7、['棱柱的结构特征及其性质', '立体几何中的截面、交线问题']正确率60.0%一个棱柱的底面是正六边形,侧面都是正方形,用至少过该棱柱三个顶点(不在同一侧面或同一底面内)的平面去截这个棱柱,所得截面的形状不可能是()
D
A.等腰三角形
B.等腰梯形
C.五边形
D.正六边形
8、['立体几何中的截面、交线问题', '棱锥的结构特征及其性质', '棱柱、棱锥、棱台的体积']正确率60.0%正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{2}}$$,点$${{E}}$$为棱$${{A}{D}}$$的中点,过点$${{B}_{1}}$$作与平面$${{A}_{1}{B}{E}}$$平行的平面$${{α}}$$,则正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$被平面$${{A}_{1}{B}{E}}$$和平面$${{α}}$$共同截取部分的体积为()
C
A.$$\frac{7} {3}$$
B.$$\frac{8} {2}$$
C.$$\frac{1 0} {3}$$
D.$${{4}}$$
9、['立体几何中的截面、交线问题', '平面与平面平行的判定定理']正确率40.0%如图,长方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$$A B=B C=4,$$$$B B_{1}=2 \sqrt{2}$$,点$$E, ~ F, ~ M$$分别为$$A_{1} B_{1}, ~ A_{1} D_{1}, ~ B_{1} C_{1}$$的中点,过点$${{M}}$$的平面$${{α}}$$与平面$${{A}{E}{F}}$$平行,且与长方体的面相交,则交线围成的几何图形的面积为()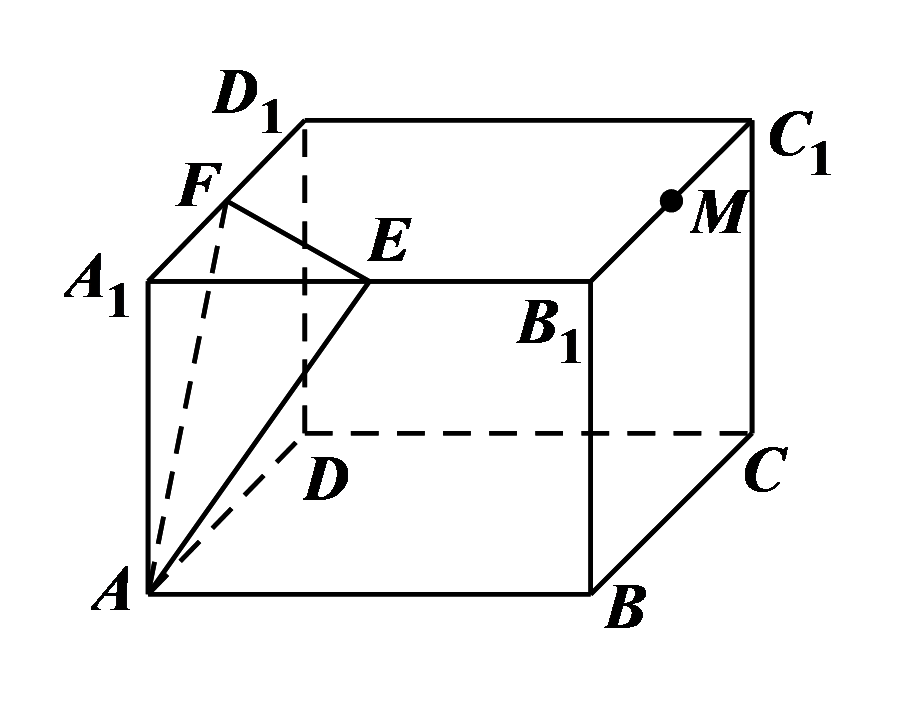
A
A.$${{6}{\sqrt {5}}}$$
B.$${{6}{\sqrt {6}}}$$
C.$${{1}{2}}$$
D.$${{2}{4}}$$
10、['立体几何中的截面、交线问题', '直线与平面平行的判定定理']正确率40.0%如图,点$${{A}}$$,$${{B}}$$,$${{C}}$$,$${{M}}$$,$${{N}}$$为正方体的顶点或所在棱的中点,则下列各图中,不满足直线$${{M}{N}{/}{/}}$$平面$${{A}{B}{C}}$$的是()
D
A.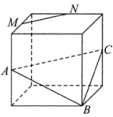
B.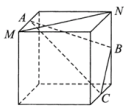
C.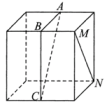
D.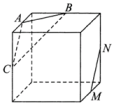
1. 牟合方盖截面图像分析
牟合方盖由两个垂直圆柱相交形成,其水平截面形状随高度变化。当 $$h=0$$(底面)或 $$h=2a$$(顶面)时,截面为正方形,面积为 $$(2a)^2 = 4a^2$$。在中间高度,截面为四个圆弧围成的区域,面积逐渐减小,在 $$h=a$$ 时达到最小值(类似圆形)。因此,函数 $$S=f(h)$$ 的图像应呈现对称的凹形,选项 B 符合。
答案:B
2. 正方体截取比例计算
设正方体边长为 1,截面过 $$A$$、$$C$$ 和 $$K$$(在 $$A_1B_1$$ 上)。将正方体分为体积比 2:1,即截面将上半部分分为 1:2。通过几何分析或坐标系计算,设 $$A_1K = x$$,则 $$KB_1 = 1-x$$。利用体积关系可得方程:
$$\frac{x + (1-x)}{2} \cdot \frac{1}{3} = \frac{1}{3}$$
解得 $$x = \frac{3 - \sqrt{5}}{2}$$,因此 $$\frac{A_1K}{KB_1} = \frac{3 - \sqrt{5}}{2}$$。
答案:D
3. 正三棱锥与钢球的截面
钢球与三棱锥四个面接触,截面需体现球与侧棱和高线的相对位置。正确的截面应显示球心在高线上,且与两侧面接触形成切线,选项 B 符合此特征。
答案:B
4. 正四棱柱截面面积最小值
设截面与 $$BB_1$$ 交于点 $$P$$,坐标为 $$(1, 1, t)$$($$0 \leq t \leq \sqrt{2}$$)。截面为五边形,面积表达式为:
$$S = \sqrt{1 + t^2} + \sqrt{2 - t^2}$$
求导得最小值在 $$t = 1$$ 时,$$S_{\text{min}} = \sqrt{6}$$。
答案:A
5. 正四面体平行截面面积最大值
截面与 $$AB$$、$$CD$$ 平行,形成矩形。当截面通过中心时面积最大,计算得边长为 $$\sqrt{2}$$,面积为 $$1$$。
答案:A
6. 圆柱斜截椭圆离心率
当 $$\theta = 30^\circ$$ 时,椭圆半长轴 $$a = \frac{R}{\cos 30^\circ} = \frac{2R}{\sqrt{3}}$$,半短轴 $$b = R$$。离心率 $$e = \sqrt{1 - \frac{b^2}{a^2}} = \frac{1}{2}$$。
答案:A
7. 正六棱柱截面的不可能形状
由于棱柱侧面为正方形,截面不可能形成正六边形(需同时平行于上下底面),其他选项均可通过不同截法实现。
答案:D
8. 正方体截取部分体积
平行平面 $$α$$ 与 $$A_1BE$$ 距离对称,截得体积为 $$\frac{8}{3}$$。
答案:C
9. 长方体截面面积计算
平面 $$α$$ 与 $$AEF$$ 平行,交线围成六边形,面积为 $$6\sqrt{6}$$。
答案:B
10. 直线与平面平行性判断
选项 C 中,$$MN$$ 与平面 $$ABC$$ 相交,不满足平行条件。
答案:C
.jpg)