正确率40.0%如图,已知在圆柱$${{O}_{1}{O}}$$中$${,{A}}$$在圆$${{O}}$$上,$$A O=1,$$$$O O_{1}=\sqrt{2},$$$${{P}{,}{Q}}$$在圆$${{O}_{1}}$$上,且满足$$P Q=\frac{2 \sqrt{3}} {3},$$则直线$${{A}{{O}_{1}}}$$与平面$${{O}{P}{Q}}$$所成角的正弦值的取值范围是()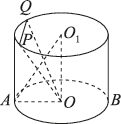
A
A.$$[ 0, \frac{3+\sqrt{6}} {6} ]$$
B.$$\left[ \frac{\sqrt{6}-3} {6}, \frac{3+\sqrt{6}} {6} \right]$$
C.$$\left[ \frac{3-\sqrt{6}} {6}, 1 \right]$$
D.$$[ 0, 1 ]$$
2、['立体几何中的探索问题']正确率40.0%如图,正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{a}{,}{E}}$$是棱$${{A}{B}}$$的中点$${,{F}}$$是侧面$${{A}{{A}_{1}}{{D}_{1}}{D}}$$内一点,若$${{E}{F}{/}{/}}$$平面$$B D D_{1} B_{1},$$且$${{E}{F}}$$长度的最大值为$${{b}{,}}$$最小值为$${\sqrt {2}{,}}$$则$${{b}^{a}{=}}$$()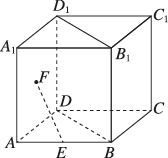
B
A.$${{7}}$$
B.$${{6}}$$
C.$${{5}}$$
D.$${{3}}$$
3、['空间直角坐标系', '立体几何中的探索问题', '空间向量运算的坐标表示', '用空间向量研究两条直线所成的角']正确率40.0%设动点$${{P}}$$是棱长为$${{1}}$$的正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的体对角线$${{B}{{D}_{1}}}$$上一点,记$$\frac{D_{1} P} {D_{1} B}=\lambda,$$当$${{∠}{A}{P}{C}}$$为钝角时$${,{λ}}$$的取值范围为()
B
A.$$( 0, \ 1 )$$
B.$$\left( \frac{1} {3}, \, 1 \right)$$
C.$$\left( 0, \enspace\frac{1} {3} \right)$$
D.$$( 1, ~ 3 )$$
4、['空间中直线与直线的位置关系', '空间中直线与平面的位置关系', '立体几何中的探索问题', '空间中平面与平面的位置关系', '两点间的距离', '棱柱、棱锥、棱台的体积', '直线与平面所成的角']正确率40.0%将一副斜边长相等的直角三角板拼接成如图所示的空间图形,其中$$A D=B D=\sqrt{2}, \, \, \, \angle A B C=6 0^{\circ}$$.若将它们的斜边$${{A}{B}}$$重合,让三角形$${{A}{B}{D}}$$以$${{A}{B}}$$为轴转动,则下列说法不正确的是()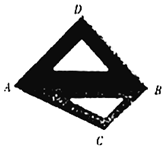
C
A.当平面$${{A}{B}{D}{⊥}}$$平面$${{A}{B}{C}}$$时,$${{C}{,}{D}}$$两点间的距离为$${\sqrt {2}}$$
B.当平面$${{A}{B}{D}{⊥}}$$平面$${{A}{B}{C}}$$时,$${{C}{D}}$$与平面$${{A}{B}{C}}$$所成的角为$${{4}{5}^{∘}}$$
C.在三角形$${{A}{B}{D}}$$转动过程中,总有$$A B \perp C D$$
D.在三角形$${{A}{B}{D}}$$转动过程中,三棱锥$$D-A B C$$的体积最大可达到$$\frac{\sqrt{3}} {6}$$
5、['立体几何中的探索问题', '其他方法求体积', '棱柱、棱锥、棱台的体积']正确率40.0%如图,正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$$a ( a > 1 )$$,动点$${{E}{,}{F}}$$在棱$${{A}_{1}{{B}_{1}}}$$上,动点$${{P}{,}{Q}}$$分别在棱$$C D, ~ A D$$上,若$$E F=1, ~ ~ A_{1} F=x,$$$$D P=y, ~ D Q=z ( x, y, z )$$均大于零$${{)}}$$,则四面体$${{P}{E}{F}{Q}}$$的体积()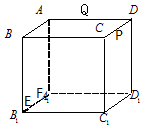
D
A.与$$x, ~ y, ~ z$$都有关
B.与$${{x}}$$有关,与$${{y}{,}{z}}$$无关
C.与$${{y}}$$有关,与$${{x}{,}{z}}$$无关
D.与$${{z}}$$有关,与$${{x}{,}{y}}$$无关
6、['立体几何中的探索问题', '直线与平面平行的判定定理', '平面与平面平行的性质定理', '直线与平面平行的性质定理', '平面与平面平行的判定定理']正确率19.999999999999996%如图,在四棱柱$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$${{A}{{A}_{1}}{⊥}}$$平面$$A B C D,$$$$A B / / C D,$$$$\angle D C B=9 0^{\circ} \,,$$$$A B=A D=A A_{1}=2 D C,$$$${{Q}}$$为棱$${{C}{{C}_{1}}}$$上一动点,过直线$${{A}{Q}}$$的平面分别与棱$$B B_{1}, ~ D D_{1}$$交于点$${{P}{,}{R}{,}}$$则下列结论中错误的是()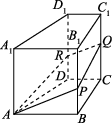
C
A.对于任意的点$${{Q}{,}}$$都有$$A P / \! / Q R$$
B.对于任意的点$${{Q}{,}}$$四边形$${{A}{P}{Q}{R}}$$不可能为平行四边形
C.存在点$${{Q}{,}}$$使得$${{△}{A}{R}{P}}$$为等腰直角三角形
D.存在点$${{Q}{,}}$$使得直线$${{B}{C}{/}{/}}$$平面$${{A}{P}{Q}{R}}$$
7、['立体几何中的探索问题', '直线与平面垂直的判定定理', '用空间向量研究空间中直线、平面的平行']正确率0.0%在棱长为$${{1}}$$的正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$${{M}}$$,$${{N}}$$分别为$${{B}{{D}_{1}}}$$,$${{B}_{1}{{C}_{1}}}$$的中点, 点$${{P}}$$在正方体的表面上运动,且满足$$M P \bot C N$$,则下列正确的是$${{(}{)}}$$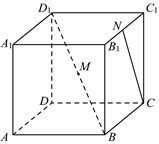
D
A.点$${{P}}$$可以是棱$${{B}{{B}_{1}}}$$的中点
B.线段$${{M}{P}}$$的最大值为$$\frac{\sqrt3} {2}$$
C.点$${{P}}$$的轨迹是正方形
D.点$${{P}}$$轨迹的长度为$${{2}{+}{\sqrt {5}}}$$
8、['立体几何中的探索问题', '直线与平面平行的判定定理', '直线与平面平行的性质定理']正确率40.0%如图所示,正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{2}}$$,$${{E}}$$,$${{F}}$$分别为$${{A}{{A}_{1}}}$$,$${{A}{B}}$$的中点,$${{M}}$$点是正方形$${{A}{B}{{B}_{1}}{{A}_{1}}}$$内的动点,若$$C_{1} M / \! /$$平面$${{C}{{D}_{1}}{E}{F}}$$,则$${{M}}$$点的轨迹长度为$${{(}{)}}$$
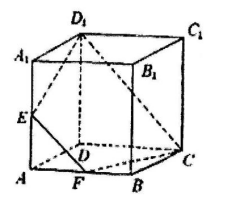
C
A.$$\frac{\sqrt2} {2}$$
B.$${{1}}$$
C.$${\sqrt {2}}$$
D. $${\sqrt {3}}$$
9、['立体几何中的探索问题', '与圆有关的轨迹问题']正确率80.0%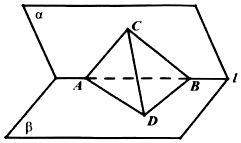 如图,二面角$$\alpha-1-\beta$$的平面角的大小为$${{6}{0}{°}}$$,$${{A}}$$,$${{B}}$$是$${{1}}$$上的两个定点,且$$A B=2. C \in\alpha$$,$${{D}{∈}{β}}$$,满足$${{A}{B}}$$与平面$${{B}{C}{D}}$$所成的角为$${{3}{0}{°}}$$,且点$${{A}}$$在平面$${{B}{C}{D}}$$上的射影$${{H}}$$在$${{△}{B}{C}{D}}$$的内部$${{(}}$$包括边界$${{)}}$$,则点$${{H}}$$的轨迹的长度等于$${{(}{)}}$$
如图,二面角$$\alpha-1-\beta$$的平面角的大小为$${{6}{0}{°}}$$,$${{A}}$$,$${{B}}$$是$${{1}}$$上的两个定点,且$$A B=2. C \in\alpha$$,$${{D}{∈}{β}}$$,满足$${{A}{B}}$$与平面$${{B}{C}{D}}$$所成的角为$${{3}{0}{°}}$$,且点$${{A}}$$在平面$${{B}{C}{D}}$$上的射影$${{H}}$$在$${{△}{B}{C}{D}}$$的内部$${{(}}$$包括边界$${{)}}$$,则点$${{H}}$$的轨迹的长度等于$${{(}{)}}$$
A
A.$$\frac{\sqrt{3} \pi} {6}$$
B.$$\frac{\pi} {3}$$
C.$$\frac{\sqrt{3} \pi} {3}$$
D.$$\frac{2 \pi} {3}$$
10、['立体几何中的探索问题']正确率40.0%在棱长为$${{4}}$$的正方体$$A B C D-A^{\prime} B^{\prime} C^{\prime} D^{\prime}$$中,$${{E}}$$、$${{F}}$$分别是$${{A}{D}}$$、$${{A}^{′}{{D}^{′}}}$$的中点,长为$${{2}}$$的线段$${{M}{N}}$$的一个端点$${{M}}$$在线段$${{E}{F}}$$上运动,另一个端点$${{N}}$$在底面$$A^{\prime} B^{\prime} C^{\prime} D^{\prime}$$上运动,则线段$${{M}{N}}$$的中点$${{P}}$$的轨迹$${{(}}$$曲面$${{)}}$$与正方体$${{(}}$$各个面$${{)}}$$所围成的几何体的体积为$${{(}{)}}$$
D
A.$$\frac{4 \pi} {3}$$
B.$$\frac{2 \pi} {3}$$
C.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
D.$$\frac{\pi} {3}$$
1. 解析:
2. 解析:
3. 解析:
4. 解析:
5. 解析:
6. 解析:
7. 解析:
8. 解析:
9. 解析:
10. 解析:
.jpg)