正确率40.0%若一个正四面体的体积为$${{V}_{1}}$$,其内切球的体积为$${{V}_{2}}$$,则$$\frac{V_{1}} {V_{2}}=( \eta)$$
A
A.$$\frac{6 \sqrt{3}} {\pi}$$
B.$$\frac{6} {\pi}$$
C.$$\frac{4} {3}$$
D.$$\frac{4 \sqrt{3}} {\pi}$$
2、['与球有关的切、接问题', '三角形的面积(公式)', '球的表面积']正确率40.0%已知三棱锥$$P-A B C$$的各顶点都在同一球面上,且$${{P}{A}{⊥}}$$平面$${{A}{B}{C}}$$,若该棱锥的体积为$${\frac{2 \sqrt{3}} {3}}, \, \, \, A B=2, \, \, \, A C=1, \, \, \angle B A C=6 0^{\circ},$$则此球的表面积等于()
B
A.$${{5}{π}}$$
B.$${{2}{0}{π}}$$
C.$${{8}{π}}$$
D.$${{1}{6}{π}}$$
3、['球的体积', '与球有关的切、接问题']正确率40.0%已知三棱锥$$A-B C D$$的外接球为球$${{O}}$$,$${{△}{B}{C}{D}}$$是边长为$${{3}{\sqrt {3}}}$$的正三角形,若三棱锥$$A-B C D$$体积的最大值为$$\frac{8 1 \sqrt{3}} {4}$$,则球$${{O}}$$的体积为()
A
A.$$\frac{5 0 0} {3} \pi$$
B.$$\frac{2 5 6} {3} \pi$$
C.$${{1}{0}{0}{π}}$$
D.$${{6}{4}{π}}$$
4、['与球有关的切、接问题', '球的表面积', '平面与平面垂直的性质定理']正确率40.0%在三棱锥$$A-B C D$$中,底面$${{B}{C}{D}}$$是边长为$${{2}{\sqrt {3}}}$$的正三角形,侧面$${{A}{B}{D}{⊥}}$$底面$${{B}{C}{D}{,}}$$且$$A B=A D=2,$$则该几何体的外接球的表面积为()
C
A.$${{1}{2}{π}}$$
B.$${{1}{6}{π}}$$
C.$${{2}{0}{π}}$$
D.$${{2}{4}{π}}$$
5、['与球有关的切、接问题', '三视图', '球的表面积']正确率60.0%如图,网格纸上小正方形的边长为$${{2}}$$,粗实线画出的是某多面体的三视图,则该多面体的外接球的表面积$${{S}{=}}$$()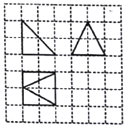
B
A.$${{4}{0}{π}}$$
B.$${{4}{1}{π}}$$
C.$${{4}{2}{π}}$$
D.$${{4}{8}{π}}$$
6、['与球有关的切、接问题', '球的结构特征及其性质', '平面与平面垂直的判定定理', '直线与平面垂直的判定定理', '直线与平面垂直的性质定理', '平面与平面垂直的性质定理']正确率40.0%过球面上一点$${{P}}$$作球的互相垂直的三条弦$$P A, ~ P B, ~ P C$$,已知$$P A=P B=2 \sqrt{2}, \; \; P C=3$$,则球的半径为()
D
A.$${{1}}$$
B.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
C.$${{2}}$$
D.$$\frac{5} {2}$$
7、['与球有关的切、接问题', '与圆有关的最值问题']正确率60.0%已知正四面体$$S-A B C$$的外接球$${{O}}$$的半径为$${\sqrt {6}{,}}$$过$${{A}{B}}$$中点$${{E}}$$作球$${{O}}$$的截面,则截面面积的最小值为()
A
A.$${{4}{π}}$$
B.$${{6}{π}}$$
C.$$\frac{1 6} {3} \pi$$
D.$$\frac{4} {3} \pi$$
8、['棱柱的结构特征及其性质', '与球有关的切、接问题', '球的结构特征及其性质', '球的表面积']正确率60.0%已知三棱柱$$A B C-A_{1} B_{1} C_{1}$$的$${{6}}$$个顶点都在球$${{O}}$$的球面上,若$$A B=3, \, \, \, A C=4, \, \, \, A B \perp A C, \, \, \, A A_{1}=5$$,则球$${{O}}$$的表面积为()
A
A.$${{5}{0}{π}}$$
B.$${{1}{0}{0}{π}}$$
C.$${{2}{0}{0}{π}}$$
D.$$\frac{1 2 5 \sqrt{2} \pi} {3}$$
9、['棱柱的结构特征及其性质', '棱锥的结构特征及其性质', '与球有关的切、接问题', '球的表面积']正确率40.0%正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$的棱长为$${{6}{,}{{O}_{1}}}$$为正方形$$A_{1} B_{1} C_{1} D_{1}$$的中心,则四棱锥$$O_{1}-A B C D$$的外接球的表面积为()
C
A.$${{9}{π}}$$
B.$${{3}{2}{4}{π}}$$
C.$${{8}{1}{π}}$$
D.$${\frac{2 4 3} {2}} \pi$$
10、['与球有关的切、接问题', '棱柱、棱锥、棱台的体积']正确率40.0%已如$${{A}}$$,$${{B}}$$,$${{C}}$$是半径为$${{1}}$$的球$${{O}}$$的球面上的三个点,且$$A C \perp B C, \, A C=B C=1$$,则三棱锥$$O-A B C$$的体积为()
A
A.$$\frac{\sqrt2} {1 2}$$
B.$$\frac{\sqrt3} {1 2}$$
C.$$\frac{\sqrt2} {4}$$
D.$$\frac{\sqrt{3}} {4}$$
1. 设正四面体的棱长为 $$a$$,其体积公式为 $$V_1 = \frac{\sqrt{2}}{12}a^3$$。内切球半径 $$r = \frac{\sqrt{6}}{12}a$$,体积为 $$V_2 = \frac{4}{3}\pi r^3 = \frac{\sqrt{6}}{54}\pi a^3$$。因此,$$\frac{V_1}{V_2} = \frac{\frac{\sqrt{2}}{12}a^3}{\frac{\sqrt{6}}{54}\pi a^3} = \frac{6\sqrt{3}}{\pi}$$。
2. 由题意,$$AB = 2$$,$$AC = 1$$,$$\angle BAC = 60^\circ$$,利用余弦定理得 $$BC = \sqrt{3}$$。由于 $$PA \perp$$ 平面 $$ABC$$,棱锥体积为 $$\frac{2\sqrt{3}}{3}$$,解得 $$PA = 2$$。将三棱锥补成长方体,其对角线为球的直径,计算得 $$2R = \sqrt{5}$$,故球的表面积为 $$5\pi$$。
3. 设外接球半径为 $$R$$,底面 $$\triangle BCD$$ 是边长为 $$3\sqrt{3}$$ 的正三角形,其外接圆半径 $$r = 3$$。三棱锥体积最大时,$$A$$ 在球心正上方或下方,此时高 $$h = R + \sqrt{R^2 - 9}$$。由体积最大值 $$\frac{81\sqrt{3}}{4}$$ 解得 $$R = 5$$,球的体积为 $$\frac{500}{3}\pi$$。
4. 底面 $$\triangle BCD$$ 是边长为 $$2\sqrt{3}$$ 的正三角形,其外接圆半径 $$r = 2$$。侧面 $$ABD \perp$$ 底面 $$BCD$$,且 $$AB = AD = 2$$,几何体的外接球半径 $$R = \sqrt{r^2 + \left(\frac{AB}{2}\right)^2} = \sqrt{5}$$,表面积为 $$20\pi$$。
5. 根据三视图还原几何体为长方体的一部分,其外接球半径通过勾股定理计算得 $$R = \sqrt{10.25}$$,表面积为 $$41\pi$$。
6. 设球的半径为 $$R$$,点 $$P$$ 到球心的距离为 $$d$$。由题意,三条弦互相垂直,利用勾股定理得 $$(2\sqrt{2})^2 + (2\sqrt{2})^2 + 3^2 = 4R^2$$,解得 $$R = \frac{5}{2}$$。
7. 正四面体外接球半径 $$R = \sqrt{6}$$,棱长为 $$4$$。过 $$AB$$ 中点 $$E$$ 的截面面积最小值为 $$\pi (R^2 - OE^2)$$,其中 $$OE = \sqrt{2}$$,故最小面积为 $$4\pi$$。
8. 三棱柱的外接球半径通过长方体的对角线计算,得 $$R = \frac{5\sqrt{2}}{2}$$,表面积为 $$50\pi$$。
9. 四棱锥 $$O_1-ABCD$$ 的外接球半径通过几何关系计算得 $$R = \frac{9}{2}$$,表面积为 $$81\pi$$。
10. 由题意,$$AC \perp BC$$,$$AC = BC = 1$$,故 $$AB = \sqrt{2}$$。球心 $$O$$ 到平面 $$ABC$$ 的距离 $$d = \sqrt{1 - \left(\frac{\sqrt{2}}{2}\right)^2} = \frac{\sqrt{2}}{2}$$。三棱锥体积为 $$\frac{1}{3} \times \frac{1}{2} \times 1 \times 1 \times \frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{12}$$。
.jpg)