正确率60.0%空间内不同的四个点,“任意三点都不共线”是“四点不共面”的()
C
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.既不充分又不必要条件
2、['立体几何中的四点共面、三点共线', '空间两直线的共面、异面问题', '充分、必要条件的判定', '基本事实1']正确率60.0%若空间中有四个点,则$${{“}}$$这四个点中有三点在同一直线上$${{”}}$$是$${{“}}$$这四个点在同一平面上$${{”}}$$的()
A
A.充分非必要条件
B.必要非充分条件
C.充要条件
D.非充分非必要条件
3、['立体几何中的四点共面、三点共线']正确率60.0%已知$$O, ~ A, ~ B, ~ C$$为空间中不共面的四点,且$$\overrightarrow{O P}=\frac{1} {3} \overrightarrow{O A}+\frac{1} {4} \overrightarrow{O B}+\lambda\overrightarrow{O C} ( \lambda\in\mathbf{R} ).$$若$$P, ~ A, ~ B, ~ C$$四点共面,则$${{λ}{=}}$$()
C
A.$$\frac{1} {3}$$
B.$$\frac{1} {4}$$
C.$$\frac{5} {1 2}$$
D.$$- \frac{7} {1 2}$$
4、['立体几何中的四点共面、三点共线']正确率60.0%已知$$A, ~ B, ~ C$$三点不共线,对于平面$${{A}{B}{C}}$$外的任意一点$${{O}{,}}$$下列条件中能确定点$$M, ~ A, ~ B, ~ C$$共面的是()
D
A.$$\overrightarrow{O M}=\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}$$
B.$$\overrightarrow{O M}=2 \overrightarrow{O A}-\overrightarrow{O B}-\overrightarrow{O C}$$
C.$$\overrightarrow{O M}=\overrightarrow{O A}+\frac{1} {2} \overrightarrow{O B}+\frac{1} {3} \overrightarrow{O C}$$
D.$$\overrightarrow{O M}=\frac{1} {3} \overrightarrow{O A}+\frac{1} {3} \overrightarrow{O B}+\frac{1} {3} \overrightarrow{O C}$$
5、['立体几何中的四点共面、三点共线']正确率60.0%已知$$A, ~ B, ~ C, ~ P$$满足任意三点不共线,但四点共面$${,{O}}$$为该平面外一点,且$$\overrightarrow{B P}=m \overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C},$$则$${{m}}$$的值为 ()
B
A.$${{−}{1}}$$
B.$${{−}{2}}$$
C.$${{−}{3}}$$
D.$${{1}}$$
6、['立体几何中的四点共面、三点共线']正确率40.0%如图所示,在正四棱柱$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$$A B=2, \, A A_{1}=\sqrt{3},$$点$${{G}}$$为正方形$${{A}{B}{C}{D}}$$的中心,$${{E}}$$为$${{A}_{1}{{D}_{1}}}$$的中点,$${{F}}$$为$${{A}{E}}$$的中点,则()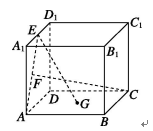
B
A.$$C, E, F, G$$四点共面,且$$C F=E G$$
B.$$C, E, F, G$$四点共面,且$$C F \neq E G$$
C.$$C, E, F, G$$四点不共面,且$$C F=E G$$
D.$$C, E, F, G$$四点不共面,且$$C F \neq E G$$
7、['立体几何中的四点共面、三点共线', '空间四边形', '基本事实1', '基本事实的推论']正确率60.0%下列命题一定正确的是()
C
A.三点确定一个平面
B.依次首尾相接的四条线段必共面
C.直线与直线外一点确定一个平面
D.两条直线确定一个平面
8、['立体几何中的四点共面、三点共线', '异面直线']正确率60.0%下列说法正确的是$${{(}{)}}$$
B
A.空间三条直线两两平行,则三条直线可确定三个平面
B.空间三条直线两两相交,且有三个交点,则这三条直线确定一个平面
C.$${{A}}$$与$${{B}}$$两点和直线$${{l}}$$距离相等,则直线$${{l}}$$和直线$${{A}{B}}$$确定一个平面
D.空间一点和一条直线可确定一个平面
9、['立体几何中的四点共面、三点共线', '基本事实3']正确率60.0%在空间四边形$${{A}{B}{C}{D}}$$的各边$$A B, ~ B C, ~ C D, ~ D A$$上的依次取点,若$${{E}{H}{、}{{F}{G}}}$$所在直线相交于点$${{P}}$$,则()

B
A.点$${{P}}$$必在直线$${{A}{C}}$$上
B.点$${{P}}$$必在直线$${{B}{D}}$$上
C.点$${{P}}$$必在平面$${{D}{B}{C}}$$外
D.点$${{P}}$$必在平面$${{A}{B}{C}}$$内
10、['立体几何中的四点共面、三点共线', '立体几何中的截面、交线问题', '其他多面体的结构特征及其性质']正确率40.0%正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$${{P}{,}{Q}}$$分别是棱$${{A}{{A}_{1}}}$$与$${{C}{{C}_{1}}}$$的中点,则经过$$P, ~ B, ~ Q$$三点的截面是($${)}$$.
A
A.菱形但不是正方形
B.邻边不相等的平行四边形
C.矩形
D.正方形
以下是各题的详细解析:
答案:$$C$$
答案:$$A$$
答案:$$C$$
答案:$$D$$
答案:$$A$$
答案:$$B$$
答案:$$C$$
答案:$$A$$
答案:$$A$$
答案:$$A$$
.jpg)