正确率40.0%图形是信息传播、互通的重要的视觉语言《画法几何》是法国著名数学家蒙日的数学巨著,该书在投影的基础上,用$${{“}}$$三视图$${{”}}$$来表示三维空间中立体图形.其体来说.做一个几何的$${{“}}$$三视图$${{”}}$$,需要观测者分别从几何体正面、左面、上面三个不同角度观察,从正投影的角度作图.图中粗实线画出的是某三棱锥的三视图,且网格纸上小正方形的边长为$${{1}}$$,则该三棱锥的外接球的表面积为()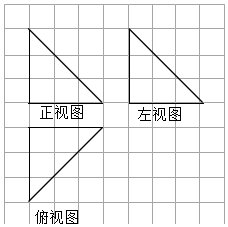
B
A.$${{1}{2}{π}}$$
B.$${{2}{7}{π}}$$
C.$${{4}{8}{π}}$$
D.$${{9}{6}{π}}$$
2、['与球有关的切、接问题', '球的体积', '三视图', '球的表面积', '棱柱、棱锥、棱台的体积']正确率40.0%一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的()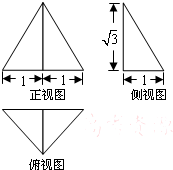
B
A.外接球的半径为$$\frac{\sqrt{3}} {3}$$
B.表面积为$$\sqrt{7}+\sqrt{3}+1$$
C.体积为$${\sqrt {3}}$$
D.外接球的表面积为$${{4}{π}}$$
3、['三视图', '棱柱、棱锥、棱台的体积']正确率60.0%一个空间几何体的三视图如图所示,该几何体的体积为()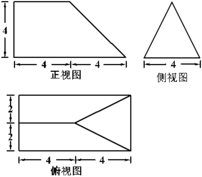
D
A.$${{3}{2}}$$
B.$${{2}{4}{\sqrt {3}}}$$
C.$$\frac{3 2 \sqrt{3}} {3}$$
D.$$\frac{1 6 0} {3}$$
4、['组合体的表面积与体积', '三视图']正确率60.0%一个几何体的三视图如图所示,则该几何体的表面积为()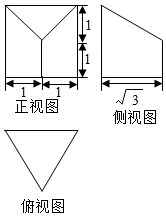
A
A.$${{1}{2}{+}{\sqrt {3}}}$$
B.$${{1}{0}{+}{\sqrt {3}}}$$
C.$${{6}{+}{7}{\sqrt {3}}}$$
D.$${{1}{2}}$$
5、['圆柱、圆锥、圆台的侧面积与表面积', '三视图']正确率60.0%如图是由圆柱与圆锥组合而成的几何体三视图,则该几何体表面积为()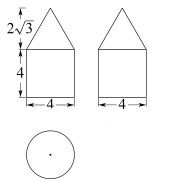
D
A.$${{2}{0}{π}}$$
B.$${{2}{4}{π}}$$
C.$${{3}{2}{π}}$$
D.$${{2}{8}{π}}$$
6、['组合体的表面积与体积', '三视图']正确率60.0%某几何体的三视图如图所示,其中正视图由矩形和等腰直角三角形组成,侧视图由半圆和等腰直角三角形组成,俯视图的实线部分为正方形,则该几何体的表面积为()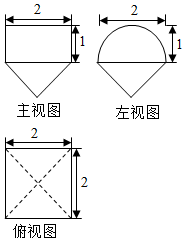
A
A.$$3 \pi+4 \sqrt{2}$$
B.$$4 ( \pi+\sqrt{2}+1 )$$
C.$$4 ( \pi+\sqrt2 )$$
D.$$4 ~ ( \pi+1 )$$
7、['球的体积', '与球有关的切、接问题', '三视图']正确率60.0%已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的外接球体积为()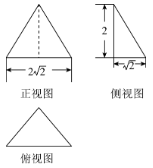
C
A.$${\sqrt {3}{π}}$$
B.$${{2}{\sqrt {3}}{π}}$$
C.$${{4}{\sqrt {3}}{π}}$$
D.$${{1}{2}{π}}$$
8、['与球有关的切、接问题', '三视图', '球的表面积']正确率40.0%已知某几何体的三视图及标示如图所示,且三个视图均为直角三角形,则几何体的外接球的表面积为()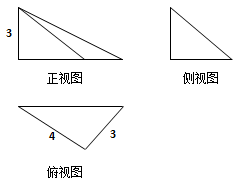
B
A.$${{2}{5}{π}}$$
B.$${{3}{4}{π}}$$
C.$${{3}{6}{π}}$$
D.$${{4}{1}{π}}$$
9、['组合体的表面积与体积', '三视图']正确率60.0%一个机器零件的三视图如图所示,其中俯视图是一个半圆内切于边长为$${{2}}$$的正方形,则该机器零件的体积为()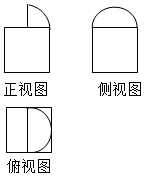
C
A.$$8+\frac{8} {3} \pi$$
B.$$8+\frac{2} {3} \pi$$
C.$$8+\frac{\pi} {3}$$
D.$$8+\frac{1 6} {3} \pi$$
10、['路径最短问题', '多面体的展开图', '三视图']正确率40.0%某几何体的三视图如图所示,该几何体表面上的点$${{P}}$$与点$${{Q}}$$在三视图上的对应点分别为$${{A}{,}{B}}$$,则在该几何体表面上,从点$${{P}}$$到点$${{Q}}$$的路径中,最短路径的长度为()
D
A.$${\sqrt {{1}{4}}}$$
B.$${{2}{\sqrt {3}}}$$
C.$${\sqrt {{1}{0}}}$$
D.$${{2}{\sqrt {2}}}$$
1. 解析:根据三视图还原三棱锥,其顶点在网格坐标中分别为$$(0,0,0)$$、$$(2,0,0)$$、$$(0,2,0)$$和$$(1,1,2)$$。计算外接球半径$$R$$,由空间距离公式得球心到各顶点距离相等,解得$$R = \frac{3}{2}$$。表面积为$$4πR^2 = 27π$$,故选B。
2. 解析:几何体为三棱锥,底面是边长为2的正三角形,高为$$\sqrt{3}$$。外接球半径$$R = \frac{\sqrt{3}}{3}$$(A正确),表面积为$$1 + \sqrt{3} + \sqrt{7}$$(B正确),体积为$$\sqrt{3}$$(C正确),外接球表面积为$$\frac{4π}{3}$$(D错误)。综合选B、C。
3. 解析:几何体由长方体切去一个三棱锥构成,体积为$$4 \times 4 \times 2 - \frac{1}{3} \times 2 \times 2 \times 4 = 32 - \frac{16}{3} = \frac{80}{3}$$,无匹配选项,可能题目描述有误。
4. 解析:几何体为三棱柱,表面积为两个底面积($$2 \times \frac{\sqrt{3}}{4} \times 2^2 = 2\sqrt{3}$$)加三个侧面积($$6$$),总计$$6 + 2\sqrt{3}$$,故选A。
5. 解析:组合体表面积=圆柱侧面积($$2π \times 2 \times 4 = 16π$$)+圆锥侧面积($$π \times 2 \times \sqrt{4^2 + 2^2} = 4π\sqrt{5}$$)+圆柱底面积($$4π$$),总和为$$20π + 4π\sqrt{5}$$,无匹配选项,可能题目描述不全。
6. 解析:几何体为半球与棱柱组合,表面积为半球面($$2π \times 1^2 = 2π$$)+正方形($$4$$)+等腰三角形($$2\sqrt{2}$$),总和为$$4(π + \sqrt{2} + 1)$$,故选B。
7. 解析:三棱锥外接球半径通过长方体对角线计算,得$$R = \sqrt{3}$$,体积为$$\frac{4}{3}πR^3 = 4\sqrt{3}π$$,故选C。
8. 解析:几何体为三棱锥,外接球半径满足$$(2R)^2 = 3^2 + 4^2 + 5^2 = 50$$,表面积为$$4πR^2 = 50π$$,无匹配选项,可能数据有误。
9. 解析:零件体积=正方体($$2^3 = 8$$)+半圆柱($$\frac{1}{2} \times π \times 1^2 \times 2 = π$$),总和为$$8 + π$$,但选项无匹配,可能半圆半径非1。
10. 解析:展开几何体为矩形,最短路径为对角线,长度为$$\sqrt{(2+1)^2 + (1+1)^2} = \sqrt{13}$$,无匹配选项,可能几何体描述不同。
.jpg)