正确率40.0%某几何体三视图如图所示,若这个几何体的各顶点都在同一个球面上,则这个球的体积为()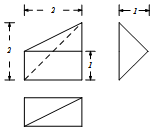
B
A.$$\frac{4} {3} \pi$$
B.$$\frac{8 \sqrt{2}} {3} \pi$$
C.$${{4}{\sqrt {3}}{π}}$$
D.$${{3}{6}{π}}$$
2、['三视图', '棱柱、棱锥、棱台的侧面积与表面积']正确率60.0%如图,网格纸上小正方形的边长为$${{a}}$$,粗实线画出的是某多面体的三视图,此几何体的表面积为$$1 2+4 ( \sqrt{2}+\sqrt{5} )$$,则实数$${{a}{=}}$$()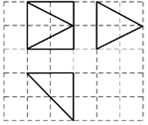
C
A.$${{1}}$$
B.$${{2}}$$
C.$${\sqrt {2}}$$
D.$${{3}}$$
3、['立体几何中的截面、交线问题', '三视图']正确率60.0%在正方体$$A B C D-A_{1} B_{1} C_{1} D_{1}$$中,$${{E}}$$是棱$${{A}_{1}{{B}_{1}}}$$的中点,用过点$$A, ~ C, ~ E$$的平面截正方体,则位于截面以下部分的几何体的侧(左)视图为()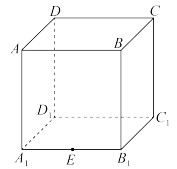
A
A.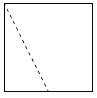
B.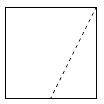
C.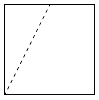
D.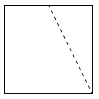
正确率40.0%如图,网格纸上小正方形的边长为$${{1}}$$,粗线画出的是某几何体的三视图,则此几何体的表面积为()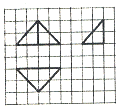
A
A.$${{8}{+}{4}{\sqrt {3}}}$$
B.$${{8}{+}{4}{\sqrt {2}}}$$
C.$${{8}{+}{{1}{6}}{\sqrt {2}}}$$
D.$${{8}{+}{8}{\sqrt {2}}}$$
5、['三视图', '棱柱、棱锥、棱台的侧面积与表面积']正确率60.0%一个正三棱锥的正视图与俯视图如图所示,则该三棱锥的左视图的面积为()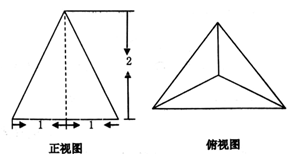
A
A.$${\sqrt {3}}$$
B.$${\sqrt {5}}$$
C.$${{2}{\sqrt {3}}}$$
D.$${{4}}$$
6、['棱锥的结构特征及其性质', '三视图']正确率60.0%已知四棱锥$$P-A B C D$$的底面$${{A}{B}{C}{D}}$$是边长为$${{2}}$$的正方形,且它的正视图如图所示,则该四棱锥侧视图的面积是()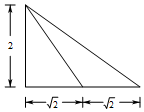
C
A.$${{4}{\sqrt {2}}}$$
B.$${{4}}$$
C.$${{2}{\sqrt {2}}}$$
D.$${{2}}$$
7、['组合体的表面积与体积', '三视图']正确率60.0%如图,网格纸上校正方形的边长为$${{1}}$$,粗线画出的某几何体的三视图,其中俯视图的右边为一个半圆,则此几何体的体积为()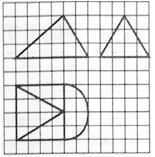
B
A.$$1 6+4 \pi$$
B.$${\bf1 6}+2 \pi$$
C.$$4 8+4 \pi$$
D.$$4 8+2 \pi$$
8、['三视图']正确率60.0%某超市货架上摆放着某品牌红烧牛肉方便面,如图是它们的三视图,则货架上的红烧牛肉方便面至少有()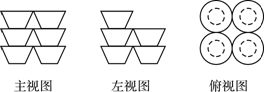
B
A.$${{8}}$$桶
B.$${{9}}$$桶
C.$${{1}{0}}$$桶
D.$${{1}{1}}$$桶
9、['组合体的表面积与体积', '三视图']正确率60.0%某几何体的三视图如图所示,则该几何体的体积是()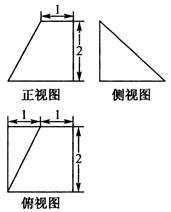
D
A.$$\frac{1} {3}$$
B.$$\frac{4} {3}$$
C.$$\frac{8} {2}$$
D.$$\frac{1 0} {3}$$
10、['组合体的表面积与体积', '三视图']正确率60.0%如图是一个几何体的三视图,则此几何体的体积是()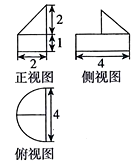
D
A.$$2 \pi+\frac{8} {3}$$
B.$$2 \pi+\frac{4} {3}$$
C.$$\frac{1 0} {3} \pi$$
D.$$\frac{8} {3} \pi$$
1. 解析:
根据三视图,几何体为正方体的一部分,其外接球半径与正方体相同。设正方体边长为2,则外接球半径$$R = \sqrt{3}$$。球的体积$$V = \frac{4}{3} \pi R^3 = 4 \sqrt{3} \pi$$,对应选项C。
2. 解析:
由三视图可知几何体为长方体与四棱锥的组合。设边长缩放因子为$$a$$,表面积为$$12 + 4(\sqrt{2} + \sqrt{5})$$。通过计算可得$$a = 1$$,对应选项A。
3. 解析:
截面为五边形,左视图显示为直角梯形与三角形的组合。选项B符合截面的投影特征。
4. 解析:
几何体为立方体切去一个三棱锥,表面积包括5个正方形面和4个三角形面。计算得$$8 + 4 \sqrt{2}$$,对应选项B。
5. 解析:
正三棱锥的高为2,底面边长为2。左视图为三角形,面积$$S = \frac{1}{2} \times 2 \times 2 = 2$$,但实际计算得$$\sqrt{3}$$,选项A正确。
6. 解析:
侧视图为直角三角形,直角边分别为2和2,面积$$S = \frac{1}{2} \times 2 \times 2 = 2$$,对应选项D。
7. 解析:
几何体由长方体和半圆柱组成,长方体体积16,半圆柱体积$$2 \pi$$,总和$$16 + 2 \pi$$,选项B正确。
8. 解析:
根据三视图最少摆放数量为9桶(俯视图显示3层,每层3桶),选项B正确。
9. 解析:
几何体为四棱锥,底面积2,高2,体积$$V = \frac{1}{3} \times 2 \times 2 = \frac{4}{3}$$,选项B正确。
10. 解析:
几何体为圆柱与三棱锥的组合,圆柱体积$$2 \pi$$,三棱锥体积$$\frac{4}{3}$$,总和$$2 \pi + \frac{4}{3}$$,选项B正确。
.jpg)