.jpg)
正确率60.0%下列命题正确的是（）
A
A.命题$${{“}}$$$${{∀}{x}{∈}{R}}$$，$${{x}^{2}{⩾}{0}}$$$${{”}}$$的否定是$${{“}}$$$${{∃}{x}{∈}{R}}$$，$${{x}^{2}{<}{0}}$$$${{”}}$$
B.若$$\overrightarrow{a} / / \overrightarrow{b}$$，$$\vec{b} / / \vec{c}$$，则$$\vec{a} / / \vec{c}$$
C.函数$$f ( x )=x^{2}-1$$的零点为$$(-1， 0 )$$，$$( 1， 0 )$$
D.$${{1}}$$弧度角表示：在任意圆中，等于半径长的弦所对的圆心角
2、['平面向量的概念'， '充分、必要条件的判定'， '向量的数量积的定义']正确率60.0%已知$$p : \overrightarrow{a}=\overrightarrow{c}， \ q : \overrightarrow{a} \cdot\overrightarrow{b}=\overrightarrow{c} \cdot\overrightarrow{b}， \ p$$是$${{q}}$$的 （）
A
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既非充分也非必要条件
3、['平面向量的概念'， '用角的终边上的点的坐标表示三角函数'， '平面向量坐标运算的综合应用']正确率60.0%已知两点$$A ~ ( 1， ~ 0 ) ~， ~ B ~ ( 1， ~ \sqrt{3} ) ~， ~ O$$为坐标原点，点$${{C}}$$在第二象限，且$$\angle A O C=1 5 0^{\circ}，$$设$$\overrightarrow{O C}=2 \overrightarrow{O A}+\lambda\overrightarrow{O B} ( \lambda\in R ) \; \;，$$则$${{λ}{=}{（}}$$）
C
A.$${{−}{1}}$$
B.$$- \frac{1} {2}$$
C.$$\frac{1} {2}$$
D.$${{1}}$$
4、['向量加法的定义及运算法则'， '向量的模'， '共线向量基本定理'， '平面向量的概念']正确率80.0%下列说法中正确的个数为（）
①如果非零向量$${{a}}$$与$${{b}}$$的方向相同或相反，那么$$( \boldsymbol{a}+\boldsymbol{b} ) / \! / \boldsymbol{a}$$；
②在平行四边形$${{A}{B}{C}{D}}$$中，必有$$\overrightarrow{B C}=\overrightarrow{A D}$$；
③若$$\overrightarrow{B C}=\overrightarrow{A D}，$$则$$A， ~ B， ~ C， ~ D$$为平行四边形的四个顶点；
④若$${{a}{，}{b}}$$均为非零向量，则$$| \boldsymbol{a}+\boldsymbol{b} | \leq| \boldsymbol{a} |+| \boldsymbol{b} |$$.
D
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
5、['点到直线的距离'， '向量加法的定义及运算法则'， '向量的模'， '平面向量的概念'， '圆上的点到直线的最大（小）距离'， '直线与圆的位置关系及其判定']正确率40.0%设$${{A}{，}{B}}$$在圆$$x^{2}+y^{2}=1$$上运动，且$$| A B |=\sqrt{3}$$，点$${{P}}$$在直线$$3 x+4 y-1 2=0$$上运动，则$$| \overrightarrow{P A}+\overrightarrow{P B} |$$的最小值为$${{(}{)}}$$
D
A.$${{3}}$$
B.$${{4}}$$
C.$$\frac{1 7} {5}$$
D.$$\frac{1 9} {5}$$
6、['向量加法的运算律'， '共线向量基本定理'， '平面向量的概念']正确率60.0%$${{{e}_{1}}^{→}{，}{{{e}_{2}}^{→}}}$$为平面的一组基底向量，已知向量$$\overrightarrow{A B}=\overrightarrow{e_{1}}-k \overrightarrow{e_{2}} \，， \， \， \overrightarrow{B C}=2 \overrightarrow{e_{1}}+\overrightarrow{e_{2}} \，， \， \， \overrightarrow{C D}=3 \overrightarrow{e_{1}}-3 \overrightarrow{e_{2}} \，，$$若$$A， B， D$$三点共线，则实数$${{k}}$$的值是（）
B
A.$${{2}}$$
B.$$\frac{2} {5}$$
C.$${{−}{2}}$$
D.$${{4}}$$
7、['平面向量的概念'， '空间向量的相关概念']正确率80.0%下列关于空间向量的命题中，正确命题的个数是$${{(}{)}}$$
①长度相等、方向相同的两个向量是相等向量；
②平行且模相等的两个向量是相等向量；
③若 $${{a}^{→}{≠}{{b}^{→}}}$$ ，则 $$| \overrightarrow{a} | \neq| \overrightarrow{b} |$$ ；
④两个向量相等，则它们的起点与终点相同．
B
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
8、['两点间的距离'， '平面向量的概念']正确率40.0%已知$$A B=3， \， \， \， A， \， \， \， B$$分别在$${{x}}$$轴和$${{y}}$$轴上滑动，$${{O}}$$为坐标原点，$$\overrightarrow{O P}=\frac{2} {3} \overrightarrow{O A}+\frac{1} {3} \overrightarrow{O B}$$，则动点$${{P}}$$的轨迹方程是$${{(}{)}}$$
A
A.$$\frac{x^{2}} {4}+y^{2}=1$$
B.$$x^{2}+\frac{y^{2}} {4}=1$$
C.$$\frac{x^{2}} {9}+y^{2}=1$$
D.$$x^{2}+\frac{y^{2}} {9}=1$$
9、['向量的数量积'， '平面向量的概念']正确率40.0%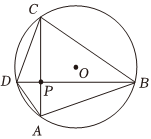
“圆幂定理”是平面几何中关于圆的一个重要定理，它包含三个结论，其中一个是相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等，如图，已知圆$${{O}}$$的半径$${{2}}$$，点$${{P}}$$是圆$${{O}}$$内的定点，且$${{O}{P}{=}{\sqrt {2}}}$$，弦$${{A}{C}}$$，$${{B}{D}}$$均过点$${{P}}$$，则下列说法错误的是$${{(}{)}}$$
A.$$\overrightarrow{P A} \cdot\overrightarrow{P C}$$为定值
B.$$\overrightarrow{O A} \cdot\overrightarrow{O C}$$的取值范围是$$[-2， 0 ]$$
C.当$$A C \perp B D$$时，$$\overrightarrow{A B} \cdot\overrightarrow{C D}$$为定值
D.$$| \overrightarrow{A C} | \cdot| \overrightarrow{B D} | < 1 6$$
10、['平面向量的概念']正确率80.0%如图，$$D， E， F$$是$${{Δ}{A}{B}{C}}$$三条边的中点，下列向量与$$\overrightarrow{D E}$$相等的向量是（）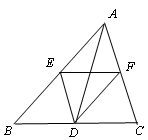
B
A.$$\overrightarrow{D F}$$
B.$$\overrightarrow{F A}$$
C.$$\overrightarrow{E F}$$
D.$$\overrightarrow{A F}$$
1. 解析：
选项A：命题的否定正确，$${{∀}{x}{∈}{R}}$$，$${{x}^{2}{⩾}{0}}$$的否定是$${{∃}{x}{∈}{R}}$$，$${{x}^{2}{<}{0}}$$。
选项B：若$$\overrightarrow{b} = \overrightarrow{0}$$，则$$\overrightarrow{a}$$与$$\overrightarrow{c}$$不一定平行，错误。
选项C：零点应为$$x=-1$$和$$x=1$$，而非点坐标，错误。
选项D：1弧度角是弧长等于半径的圆心角，而非弦长，错误。
正确答案：A
2. 解析：
若$$\overrightarrow{a} = \overrightarrow{c}$$，则$$\overrightarrow{a} \cdot \overrightarrow{b} = \overrightarrow{c} \cdot \overrightarrow{b}$$，即$$p \Rightarrow q$$。
但$$\overrightarrow{a} \cdot \overrightarrow{b} = \overrightarrow{c} \cdot \overrightarrow{b}$$时，$$\overrightarrow{a}$$与$$\overrightarrow{c}$$不一定相等（如$$\overrightarrow{b} = \overrightarrow{0}$$），即$$q \nRightarrow p$$。
因此$$p$$是$$q$$的充分不必要条件。
正确答案：A
3. 解析：
由题意，$$\overrightarrow{OA} = (1, 0)$$，$$\overrightarrow{OB} = (1, \sqrt{3})$$。
设$$\overrightarrow{OC} = (x, y)$$，则$$x = 2 \cdot 1 + \lambda \cdot 1 = 2 + \lambda$$，$$y = 0 + \lambda \cdot \sqrt{3} = \lambda \sqrt{3}$$。
因$$\angle AOC = 150^\circ$$，$$\tan 150^\circ = \frac{y}{x} = -\frac{1}{\sqrt{3}}$$，代入得$$\frac{\lambda \sqrt{3}}{2 + \lambda} = -\frac{1}{\sqrt{3}}$$，解得$$\lambda = -1$$。
正确答案：A
4. 解析：
①正确，$$(\boldsymbol{a}+\boldsymbol{b})$$与$$\boldsymbol{a}$$方向相同或相反时平行。
②正确，平行四边形对边向量相等。
③错误，$$A, B, C, D$$可能共线。
④正确，向量加法满足三角不等式。
正确答案：D（3个正确）
5. 解析：
圆心为原点，$$|AB|=\sqrt{3}$$，则弦$$AB$$对应的圆心角为$$120^\circ$$。
设$$M$$为$$AB$$中点，则$$|OM| = \sqrt{1 - (\frac{\sqrt{3}}{2})^2} = \frac{1}{2}$$。
$$|\overrightarrow{PA} + \overrightarrow{PB}| = 2|\overrightarrow{PM}|$$，最小值为$$2 \cdot \left(\frac{|3 \cdot 0 + 4 \cdot 0 - 12|}{5} - \frac{1}{2}\right) = 2 \cdot \left(\frac{12}{5} - \frac{1}{2}\right) = \frac{19}{5}$$。
正确答案：D
6. 解析：
由$$A, B, D$$共线，$$\overrightarrow{AD} = \overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CD} = (1+2+3)\overrightarrow{e_1} + (-k+1-3)\overrightarrow{e_2} = 6\overrightarrow{e_1} + (-k-2)\overrightarrow{e_2}$$。
$$\overrightarrow{AB} = \overrightarrow{e_1} - k\overrightarrow{e_2}$$，共线则$$\frac{6}{1} = \frac{-k-2}{-k}$$，解得$$k=2$$。
正确答案：A
7. 解析：
①正确，长度和方向相同即为相等向量。
②错误，方向可能相反。
③错误，向量不等但模可能相等。
④错误，向量相等不要求起点和终点相同。
正确答案：B（仅①正确）
8. 解析：
设$$A(a, 0)$$，$$B(0, b)$$，则$$a^2 + b^2 = 9$$。
$$\overrightarrow{OP} = \frac{2}{3}(a, 0) + \frac{1}{3}(0, b) = \left(\frac{2a}{3}, \frac{b}{3}\right)$$。
设$$P(x, y)$$，则$$x = \frac{2a}{3}$$，$$y = \frac{b}{3}$$，即$$a = \frac{3x}{2}$$，$$b = 3y$$。
代入得$$\left(\frac{3x}{2}\right)^2 + (3y)^2 = 9$$，化简得$$\frac{x^2}{4} + y^2 = 1$$。
正确答案：A
9. 解析：
圆幂定理：$$PA \cdot PC = PB \cdot PD = r^2 - OP^2 = 4 - 2 = 2$$（定值），A正确。
$$\overrightarrow{OA} \cdot \overrightarrow{OC} = |OA||OC|\cos \theta = 4 \cos \theta$$，$$\theta \in [90^\circ, 180^\circ]$$，范围为$$[-4, 0]$$，B错误。
当$$AC \perp BD$$时，$$\overrightarrow{AB} \cdot \overrightarrow{CD} = 0$$（定值），C正确。
$$|AC| \cdot |BD| \leq \left(\frac{|AC| + |BD|}{2}\right)^2 \leq 16$$，但$$AC$$和$$BD$$不能同时为直径，D正确。
正确答案：B
10. 解析：
$$\overrightarrow{DE}$$为$$\triangle ABC$$的中位线，方向与$$\overrightarrow{AC}$$相同。
$$\overrightarrow{AF}$$为从$$A$$指向$$F$$（$$BC$$中点），与$$\overrightarrow{DE}$$方向相同且长度相等。
正确答案：D