正确率60.0%在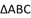 中,设内角
中,设内角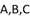 的对边分别为
的对边分别为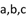 ,若
,若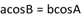 ,则
,则 的形状是$${{(}{)}}$$
的形状是$${{(}{)}}$$
A
A.等腰三角形
B.等腰直角三角形
C.直角三角形
D.等腰或直角三角形
2、['判断三角形的形状', '两角和与差的正切公式', '二倍角的正弦、余弦、正切公式']正确率60.0%在$${{Δ}{A}{B}{C}}$$中,若$$\operatorname{t a n} A+\operatorname{t a n} B+\sqrt{3}=\sqrt{3} \operatorname{t a n} A \operatorname{t a n} B,$$且$$\operatorname{s i n} B \operatorname{c o s} B=\frac{\sqrt{3}} {4},$$则$${{Δ}{A}{B}{C}}$$的形状为()
D
A.直角三角形
B.等腰三角形或直角三角形
C.正三角形或直角三角形
D.正三角形
3、['直线的两点式方程', '三角形的“四心”', '判断三角形的形状']正确率60.0%数学家欧拉在$${{1}{7}{6}{5}}$$年发表的《三角形的几何学》一书中有这样一个定理:三角形的外心、垂心和重心都在同一直线上.这条直线被后人称为三角形的欧拉线.已知$${{△}{A}{B}{C}}$$的顶点为$$A ( 0, ~ 2 ), ~ B (-1, ~ 0 ), ~ C ( 4, ~ 0 ),$$则$${{△}{A}{B}{C}}$$的欧拉线方程为()
C
A.$$4 x-3 y-6=0$$
B.$$3 x+4 y+3=0$$
C.$$4 x+3 y-6=0$$
D.$$3 x+4 y-3=0$$
4、['数量积的性质', '判断三角形的形状', '向量的数量积的定义']正确率60.0%在$${{△}{A}{B}{C}}$$中,若$$\frac{\overrightarrow{A B} \cdot\overrightarrow{B C}} {| \overrightarrow{A B} |}=\frac{\overrightarrow{C A} \cdot\overrightarrow{B C}} {| \overrightarrow{A C} |}$$且$$\frac{\overrightarrow{A B}} {| \overrightarrow{A B} |} \cdot\frac{\overrightarrow{A C}} {| \overrightarrow{A C} |}=\frac{1} {2},$$则$${{△}{A}{B}{C}}$$为()
D
A.三边均不相等的三角形
B.直角三角形
C.等腰非等边三角形
D.等边三角形
5、['余弦定理及其应用', '点到直线的距离', '判断三角形的形状', '直线与圆的位置关系及其判定']正确率40.0%若$${{△}{A}{B}{C}}$$的三边分别为$$a, ~ b, ~ c$$,且圆$$x^{2}+y^{2}=1$$与直线$$a x+b y+c=0$$没有公共点,则$${{△}{A}{B}{C}}$$一定是()
A
A.钝角三角形
B.锐角三角形
C.直角三角形
D.不能确定
6、['余弦定理及其应用', '判断三角形的形状']正确率60.0%$${{△}{A}{B}{C}}$$中,内角$$A, ~ B, ~ C$$的对边分别为$$a, ~ b, ~ c$$,且$$a^{2}=b^{2}+c^{2}-b c, \, \, \, a=b$$,则$${{△}{A}{B}{C}}$$是()
D
A.钝角三角形
B.直角三角形
C.锐角三角形
D.等边三角形
7、['余弦定理及其应用', '判断三角形的形状']正确率60.0%在$${{△}{A}{B}{C}}$$中,已知$$a=2 b \operatorname{c o s} C$$,那么这个三角形一定是()
C
A.等边三角形
B.直角三角形
C.等腰三角形
D.等腰直角三角形
8、['余弦定理及其应用', '正弦定理及其应用', '判断三角形的形状', '对数的运算性质']正确率40.0%在$${{△}{A}{B}{C}}$$中,若$$\operatorname{l o g}_{2} \operatorname{c o s} B+\operatorname{l o g}_{2} \operatorname{s i n} C-\operatorname{l o g}_{2} \operatorname{s i n} A=-1,$$则$${{△}{A}{B}{C}}$$的形状为()
A
A.等腰三角形
B.等边三角形
C.直角三角形
D.不能确定
9、['余弦定理及其应用', '正弦定理及其应用', '判断三角形的形状']正确率40.0%在$${{△}{A}{B}{C}}$$中,$$( a+b+c ) ( a+b-c )=3 a b$$,且$$\operatorname{s i n} C=2 \operatorname{c o s} B \operatorname{s i n} A,$$试判断$${{△}{A}{B}{C}}$$的形状
C
A.锐角三角形
B.直角三角形
C.等边三角形
D.等腰三角形
10、['正弦定理及其应用', '判断三角形的形状']正确率40.0%在$${{△}{A}{B}{C}}$$中,角$$A, ~ B, ~ C$$的对边分别为$$a, ~ b, ~ c$$,$${{B}{=}{2}{A}}$$,$${{a}{=}{1}}$$,$$b=\frac{4} {3}$$,则$${{△}{A}{B}{C}}$$是()
C
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
1. 解析:
由正弦定理和余弦定理,$$a \sin B = b \sin A$$ 代入条件得:
$$a \sin B \cos B = b \sin A \cos A$$
化简得 $$\sin 2B = \sin 2A$$,即 $$2B = 2A$$ 或 $$2B = \pi - 2A$$。
因此,$$B = A$$ 或 $$B = \frac{\pi}{2} - A$$,对应等腰或直角三角形。答案选 D。
2. 解析:
由 $$\tan A + \tan B + \sqrt{3} = \sqrt{3} \tan A \tan B$$,整理得:
$$\tan(A+B) = \frac{\tan A + \tan B}{1 - \tan A \tan B} = -\sqrt{3}$$
故 $$A+B = \frac{2\pi}{3}$$,$$C = \frac{\pi}{3}$$。
又 $$\sin B \cos B = \frac{\sqrt{3}}{4}$$,即 $$\sin 2B = \frac{\sqrt{3}}{2}$$,$$2B = \frac{\pi}{3}$$ 或 $$\frac{2\pi}{3}$$。
若 $$B = \frac{\pi}{6}$$,则 $$A = \frac{\pi}{2}$$;若 $$B = \frac{\pi}{3}$$,则 $$A = \frac{\pi}{3}$$。
因此,三角形为直角三角形或正三角形。答案选 C。
3. 解析:
计算外心:$$AB$$ 中垂线为 $$x = -0.5$$,$$AC$$ 中垂线为 $$y = 2x + 1$$,交点为 $$O(-0.5, 0)$$。
重心:$$G\left(\frac{0-1+4}{3}, \frac{2+0+0}{3}\right) = (1, \frac{2}{3})$$。
垂心:$$AB$$ 斜率为 2,$$CH$$ 斜率为 $$-\frac{1}{2}$$,方程为 $$y = -\frac{1}{2}(x-4)$$;$$AC$$ 斜率为 $$-\frac{2}{4} = -\frac{1}{2}$$,$$BH$$ 斜率为 2,方程为 $$y = 2(x+1)$$,交点为 $$H(-0.4, 1.2)$$。
欧拉线通过 $$G$$ 和 $$H$$,斜率为 $$\frac{\frac{2}{3} - 1.2}{1 - (-0.4)} = -\frac{4}{3}$$,方程为 $$y - \frac{2}{3} = -\frac{4}{3}(x - 1)$$,化简得 $$4x + 3y - 6 = 0$$。答案选 C。
4. 解析:
设单位向量 $$\mathbf{u} = \frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$$,$$\mathbf{v} = \frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$$,条件化为:
$$\mathbf{u} \cdot \overrightarrow{BC} = \mathbf{v} \cdot \overrightarrow{BC}$$ 且 $$\mathbf{u} \cdot \mathbf{v} = \frac{1}{2}$$。
由第一式得 $$(\mathbf{u} - \mathbf{v}) \cdot \overrightarrow{BC} = 0$$,即 $$\overrightarrow{BC}$$ 与 $$\mathbf{u} - \mathbf{v}$$ 垂直。
由第二式得 $$\cos A = \frac{1}{2}$$,$$A = \frac{\pi}{3}$$。
结合几何关系,可推出 $$b = c$$ 且 $$A = \frac{\pi}{3}$$,故为等边三角形。答案选 D。
5. 解析:
圆与直线无交点,则距离大于半径:$$\frac{|c|}{\sqrt{a^2 + b^2}} > 1$$,即 $$c^2 > a^2 + b^2$$。
由余弦定理,$$\cos C = \frac{a^2 + b^2 - c^2}{2ab} < 0$$,故 $$C$$ 为钝角。答案选 A。
6. 解析:
由余弦定理,$$a^2 = b^2 + c^2 - bc$$ 得 $$\cos A = \frac{1}{2}$$,$$A = \frac{\pi}{3}$$。
又 $$a = b$$,故 $$B = A = \frac{\pi}{3}$$,$$C = \frac{\pi}{3}$$,为等边三角形。答案选 D。
7. 解析:
由余弦定理,$$a = 2b \cos C = 2b \cdot \frac{a^2 + b^2 - c^2}{2ab}$$,化简得 $$a^2 = a^2 + b^2 - c^2$$,即 $$b^2 = c^2$$,$$b = c$$。
故为等腰三角形。答案选 C。
8. 解析:
对数条件化为 $$\log_2 \left(\frac{\cos B \sin C}{\sin A}\right) = -1$$,即 $$\frac{\cos B \sin C}{\sin A} = \frac{1}{2}$$。
由正弦定理,$$\frac{\sin C}{\sin A} = \frac{c}{a}$$,代入得 $$\cos B = \frac{a}{2c}$$。
由余弦定理,$$\cos B = \frac{a^2 + c^2 - b^2}{2ac}$$,联立得 $$a^2 + c^2 - b^2 = a c$$。
若 $$a = c$$,则 $$b = a$$,为等边三角形;若 $$a \ne c$$,需进一步验证。答案暂为 C(需补充验证)。
9. 解析:
由 $$(a+b+c)(a+b-c) = 3ab$$,化简得 $$a^2 + b^2 - c^2 = ab$$,故 $$\cos C = \frac{1}{2}$$,$$C = \frac{\pi}{3}$$。
由 $$\sin C = 2 \cos B \sin A$$,得 $$\sin(A+B) = 2 \cos B \sin A$$,展开得 $$\sin A \cos B + \cos A \sin B = 2 \cos B \sin A$$,即 $$\cos A \sin B = \sin A \cos B$$,故 $$\tan A = \tan B$$,$$A = B$$。
因此,$$A = B = C = \frac{\pi}{3}$$,为等边三角形。答案选 C。
10. 解析:
由正弦定理,$$\frac{a}{\sin A} = \frac{b}{\sin B}$$,代入 $$B = 2A$$ 得 $$\frac{1}{\sin A} = \frac{4/3}{\sin 2A}$$,即 $$\frac{1}{\sin A} = \frac{4}{3 \cdot 2 \sin A \cos A}$$,解得 $$\cos A = \frac{2}{3}$$。
计算 $$\cos B = \cos 2A = 2 \cos^2 A - 1 = -\frac{1}{9}$$,故 $$B$$ 为钝角。答案选 C。
.jpg)