正确率40.0%已知$${{△}{A}{B}{C}}$$中,内角$$A, ~ B, ~ C$$所对的边分别为$$a, ~ b, ~ c$$,若$$\frac{b} {c}=\frac{\operatorname{c o s} A} {1+\operatorname{c o s} C},$$则$$\operatorname{s i n} \, ( 2 A+\frac{\pi} {6} )$$的取值范围是()
B
A.$$( \mathrm{\Pi-\frac{1} {2}, \ \frac{1} {2}} )$$
B.$$\varsigma-\frac{1} {2}, \ 1 ]$$
C.$$( \; \frac{1} {2}, \; 1 ]$$
D.$$[-1, ~ \frac{1} {2} )$$
2、['正切(型)函数的单调性', '正弦定理及其应用', '正切(型)函数的定义域与值域', '解三角形中的最值(范围)问题', '二倍角的正弦、余弦、正切公式']正确率40.0%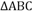 的三个内角
的三个内角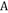 ,
,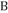 ,
,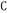 的对边分别为
的对边分别为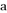 ,
,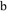 ,
,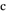 ,若
,若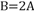 ,
,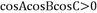 ,则
,则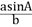 的取值范围是
的取值范围是
D
A.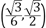
B.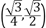
C.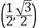
D.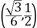
正确率40.0%设锐角三角形$${{A}{B}{C}}$$的内角$$A, ~ B, ~ C$$的对边分别为$$a, ~ b, ~ c,$$若$$\mathrm{c o s} B+\sqrt{3} \mathrm{s i n} B=2, \, \, \, c=2,$$则$${{△}{A}{B}{C}}$$的面积的取值范围为()
B
A.$$\left( \frac{\sqrt{3}} {2}, ~ 4 \sqrt{3} \right)$$
B.$$\left( \frac{\sqrt{3}} {2}, ~ 2 \sqrt{3} \right)$$
C.$$\left( \frac{\sqrt{3}} {4}, ~ \sqrt{3} \right)$$
D.$$\left( \frac{\sqrt{3}} {8}, \ \frac{\sqrt{3}} {4} \right)$$
4、['解三角形中的最值(范围)问题', '直线的斜率']正确率40.0%在平面直角坐标系$${{x}{O}{y}}$$中,$$A (-1, 0 ), \, \, \, B ( 1, 0 ), \, \, \, C ( 0, 1 )$$,经过原点的直线$${{l}}$$将$${{△}{A}{B}{C}}$$分成左$${、}$$右两部分,记左$${、}$$右两部分的面积分别为$${{S}_{1}{、}{{S}_{2}}}$$,则$$\frac{( 1+S_{1} )^{2}} {1-S_{2}^{2}}$$取得最小值时,直线$${{l}}$$的斜率$${{(}{)}}$$
D
A.等于$${{1}}$$
B.等于$${{−}{1}}$$
C.等于$$\frac{1} {2}$$
D.不存在
5、['解三角形中的最值(范围)问题']正确率60.0%在$${{△}}$$$${{A}{B}{C}}$$中,角$$A, B, C$$所对的边分别为$$a, b, c$$,已知$$B=6 0^{\circ}, b=4$$,则$${{△}}$$$${{A}{B}{C}}$$面积的最大值为()
B
A.$${{3}{\sqrt {3}}}$$
B.$${{4}{\sqrt {3}}}$$
C.$${{5}{\sqrt {3}}}$$
D.$${{6}}$$
6、['余弦定理及其应用', '解三角形中的最值(范围)问题', '等比数列的定义与证明', '利用基本不等式求最值']正确率40.0%在$${{△}{A}{B}{C}}$$中,角$$A, ~ B, ~ C$$所对的边$$a, ~ b, ~ c$$成等比数列,则角$${{B}}$$的取值范围是$${{(}{)}}$$
C
A.$$[ \frac{\pi} {3}, \pi)$$
B.$$[ \frac{\pi} {6}, \pi)$$
C.$$( 0, \frac{\pi} {3} ]$$
D.$$( 0, \frac{\pi} {6} ]$$
7、['余弦定理及其应用', '解三角形中的最值(范围)问题', '利用基本不等式求最值']正确率60.0%$${{△}{A}{B}{C}}$$的内角$$A, ~ B, ~ C$$所对的边分别是$$a, ~ b, ~ c$$.已知$${\frac{b} {c}} \operatorname{c o s} C+{\frac{b} {a}} \operatorname{c o s} A=1,$$则$${{c}{o}{s}{B}}$$的最小值为$${{(}{)}}$$
D
A.$$\frac{\sqrt{3}} {3}$$
B.$$\frac{1} {3}$$
C.$$\frac{\sqrt2} {2}$$
D.$$\frac{1} {2}$$
8、['余弦定理及其应用', '三角形的面积(公式)', '解三角形中的最值(范围)问题', '利用基本不等式求最值']正确率40.0%$${{△}{A}{B}{C}}$$的内角$$A, ~ B, ~ C$$的对边为$$a, ~ b, ~ c$$,若$${{△}{A}{B}{C}}$$的面积为$$- \frac{\sqrt{3}} {4} ( a^{2}+c^{2}-b^{2} ), \, \, b=2 \sqrt{3}$$,则$${{a}{+}{c}}$$的最大值为()
D
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
9、['余弦定理及其应用', '椭圆的定义', '解三角形中的最值(范围)问题', '二次函数的图象分析与判断']正确率40.0%在$${{△}{A}{B}{C}}$$中,$$A B+A C=8, \, \, \, B C=4, \, \, \, D$$为$${{B}{C}}$$的中点,当$${{A}{D}}$$长度最小时,$${{△}{A}{B}{C}}$$的面积为()
D
A.$${{2}{\sqrt {2}}}$$
B.$${{4}}$$
C.$${{4}{\sqrt {2}}}$$
D.$${{4}{\sqrt {3}}}$$
10、['余弦定理及其应用', '正弦定理及其应用', '解三角形中的最值(范围)问题']正确率40.0%已知$$a, ~ b, ~ c$$分别为$${{△}{A}{B}{C}}$$三个内角$$A. ~ B. ~ C$$的对边,且$$\frac{\operatorname{s i n} A-\operatorname{s i n} B} {\operatorname{s i n} C} \geqslant\frac{c-b} {a+b}$$,则()
D
A.$${{A}}$$的最大值为$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
B.$${{A}}$$的最小值为$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
C.$${{A}}$$的最大值为$$\frac{\pi} {3}$$
D.$${{A}}$$的最小值为$$\frac{\pi} {3}$$
1. 解析:
2. 解析:
3. 解析:
4. 解析:
- 直线与 $$AC$$ 相交:$$S_1$$ 为左侧面积,$$S_2$$ 为右侧面积。
- 直线与 $$BC$$ 相交:类似计算。
5. 解析:
6. 解析:
7. 解析:
8. 解析:
9. 解析:
10. 解析:
.jpg)