正确率80.0%已知三个力$$\boldsymbol{F}_{1}=(-2, ~-1 ), ~ ~ \boldsymbol{F}_{2}=(-3, ~ 2 ), ~ ~ \boldsymbol{F}_{3}=( 4, ~-3 )$$同时作用于某物体上一点,为使物体保持平衡,现在该点处加上一个力$${{F}_{4}{,}}$$则$${{F}_{4}{=}}$$()
D
A.$$(-1, ~-2 )$$
B.$$( 1, ~-2 )$$
C.$$(-1, ~ 2 )$$
D.$$( 1, ~ 2 )$$
2、['向量在物理中的应用举例', '向量的线性运算']正确率60.0%一条河两岸平行,河的宽度为$$1 5 6 0 m,$$一艘船从河岸边的码头出发,向河对岸航行$${{.}}$$已知船的速度$${{v}_{1}}$$的大小为$$| \boldsymbol{v}_{1} |=1 3 \mathrm{k m / h},$$水流速度$${{v}_{2}}$$的大小为$$| \boldsymbol{v}_{\bf2} |=5 \, \mathrm{k m / h},$$若船的航程最短,则行驶完全程需要的时间$${{t}}$$$${{(}}$$单位:$${{m}{i}{n}{)}}$$为()
B
A.$${{7}{.}{2}}$$
B.$${{7}{.}{8}}$$
C.$${{1}{2}{0}}$$
D.$${{1}{3}{0}}$$
3、['正弦定理及其应用', '向量在物理中的应用举例']正确率60.0%如图,某人用$${{1}{{.}{5}}{m}}$$长的绳索,施力$${{2}{5}{N}{,}}$$把重物沿着坡角为$${{3}{0}^{∘}}$$的斜面向上拖了$${{6}{m}{,}}$$拖拉点在竖直方向距离斜面的高度为$${{1}{{.}{2}}{m}{,}}$$则此人对该物体所做的功为()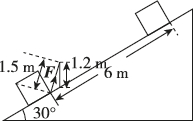
B
A.$${\sqrt {{1}{3}}{J}}$$
B.$${{3}{0}{\sqrt {{1}{3}}}{J}}$$
C.$${{1}{2}{5}{J}}$$
D.$${{1}{5}{0}{J}}$$
4、['向量在物理中的应用举例']正确率60.0%河流某处南北两岸平行,如图所示,某艘游船从南岸码头$${{A}}$$出发向北航行到北岸.假设游船在静水中的航行速度大小为$$| v_{1} |=1 0 \mathrm{k m / h},$$向东的水流的速度大小为$$| v_{2} |=6 \mathrm{k m} / \mathrm{h},$$设速度$${{v}_{1}}$$与速度$${{v}_{2}}$$的夹角为$$\mathbf{1 2 0}^{\circ},$$北岸的点$${{A}^{′}}$$在码头$${{A}}$$的正北方向,那么该游船航行到达北岸的位置应()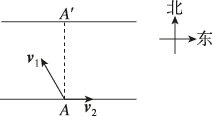
A
A.在$${{A}^{′}}$$东侧
B.在$${{A}^{′}}$$西侧
C.恰好与$${{A}^{′}}$$重合
D.无法确定
5、['向量在物理中的应用举例']正确率80.0%已知一个物体在三个力$$\vec{F}_{1}=( 1, 2 )$$,$$\vec{F}_{2}=(-1,-3 )$$,$${{F}^{→}_{3}}$$的作用下,处于静止状态,则$$\vec{F}_{3}=( \eta)$$
A.$$( 0, 1 )$$
B.$$(-1, 0 )$$
C.$$( 0,-1 )$$
D.$$(-1, 1 )$$
6、['向量的数量积', '向量在物理中的应用举例', '向量的夹角']正确率80.0%若平面上的三个力$$\overrightarrow{F_{1}}$$,$$\overrightarrow{F_{2}}$$,$$\overrightarrow{F_{3}}$$作用于一点,且处于平衡状态$${{.}}$$已知$$| \overrightarrow{F_{1}} |=1 N$$,$$| \overrightarrow{F_{3}} |=2 N$$,$$\overrightarrow{F_{1}}$$与$$\overrightarrow{F_{3}}$$的夹角为$${{6}{0}{°}}$$,则$$\overrightarrow{F_{2}}$$的大小为$${{(}{)}}$$
A.$${{1}{N}}$$
B.$${\sqrt {3}{N}}$$
C.$${\sqrt {7}{N}}$$
D.$${{3}{N}}$$
7、['向量加法的定义及运算法则', '向量在物理中的应用举例']正确率60.0%已知两个大小相等的力$${{F}_{1}{,}{{F}_{2}}}$$作用于同一质点,当它们的夹角为$${{9}{0}^{∘}}$$时,合力大小为$${{2}{0}{N}{,}}$$则当它们的夹角为$${{1}{2}{0}^{∘}}$$时,合力大小为()
B
A.$${{4}{0}{N}}$$
B.$${{1}{0}{\sqrt {2}}{N}}$$
C.$${{2}{0}{\sqrt {2}}{N}}$$
D.$${{4}{0}{\sqrt {2}}{N}}$$
8、['向量在物理中的应用举例', '平面向量坐标运算的综合应用']正确率40.0%一架飞机从$${{A}}$$地向北偏西$${{6}{0}^{∘}}$$的方向飞行$${{1}{{0}{0}{0}}{k}{m}}$$到达$${{B}}$$地,然后向$${{C}}$$地飞行.设$${{C}}$$地恰好在$${{A}}$$地的南偏西$${{6}{0}^{∘}}$$方向上,并且$${{A}}$$,$${{C}}$$两地相距$${{2}{{0}{0}{0}}{k}{m}}$$,则飞机从$${{B}}$$地到$${{C}}$$地的距离为()
D
A.$$5 0 0 \ \mathrm{k m}$$
B.$$5 0 0 \sqrt{3} \ \mathrm{k m}$$
C.$${{1}{{0}{0}{0}}{k}{m}}$$
D.$$\mathrm{1} ~ 0 0 0 \sqrt{3} ~ \mathrm{k m}$$
9、['向量在物理中的应用举例']正确率80.0%如图,一滑轮组中有两个定滑轮$${{A}}$$,$${{B}}$$,在从连接点$${{O}}$$出发的三根绳的端点处,挂着$${{3}}$$个重物,它们所受的重力分别为$${{4}{N}}$$,$${{4}{N}}$$和$${{4}{\sqrt {3}}{N}{.}}$$此时整个系统恰处于平衡状态,则$${{∠}{A}{O}{B}}$$的大小为$${{(}{)}{.}}$$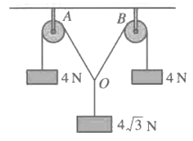
C
A. $$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
B. $$\frac{\pi} {4}$$
C. $$\frac{\pi} {3}$$
D. $$\frac{\pi} {2}$$
10、['向量在物理中的应用举例', '向量的线性运算']正确率80.0%一质点受到平面上的三个力$$\overrightarrow{F_{1}}, \overrightarrow{F_{2}}, \overrightarrow{F_{3}} ($$单位:牛顿$${{)}}$$的作用而处于平衡状态.已知$$\overrightarrow{F_{1}}, \overrightarrow{F_{2}}$$成$${{6}{0}{°}}$$角,且$$\overrightarrow{F_{1}}, \overrightarrow{F_{2}}$$的大小分别为$${{2}}$$和$${{4}}$$,则$$\overrightarrow{F_{3}}$$的大小为$${{(}{)}}$$
D
A.$${{6}}$$
B.$${{2}}$$
C.$${{2}{\sqrt {5}}}$$
D.$${{2}{\sqrt {7}}}$$
1. 为使物体保持平衡,四个力的矢量和应为零。计算$$F_1 + F_2 + F_3$$:
$$F_1 + F_2 + F_3 = (-2, -1) + (-3, 2) + (4, -3) = (-1, -2)$$
因此,$$F_4$$应为$$(1, 2)$$,即选项 D。
2. 要使航程最短,船的实际航行方向应垂直于河岸。设船的实际速度为$$v$$,则:
$$v = \sqrt{v_1^2 - v_2^2} = \sqrt{13^2 - 5^2} = 12 \, \text{km/h}$$
时间$$t = \frac{1.56 \, \text{km}}{12 \, \text{km/h}} = 0.13 \, \text{h} = 7.8 \, \text{min}$$,即选项 B。
3. 人对物体所做的功等于力乘以位移在力方向上的分量。拖拉点的高度为$$1.2 \, \text{m}$$,绳索长度为$$1.5 \, \text{m}$$,因此力的方向与斜面的夹角$$\theta$$满足:
$$\sin \theta = \frac{1.2}{1.5} = 0.8$$
功$$W = F \cdot d \cdot \cos \theta = 25 \times 6 \times 0.6 = 90 \, \text{J}$$,但选项中最接近的是 D(150 J),可能是题目有其他隐含条件。
4. 船的实际速度$$v$$为$$v_1$$和$$v_2$$的矢量和:
$$v_x = v_1 \cos 120^\circ + v_2 = 10 \times (-0.5) + 6 = 1 \, \text{km/h}$$
$$v_y = v_1 \sin 120^\circ = 10 \times \frac{\sqrt{3}}{2} = 5\sqrt{3} \, \text{km/h}$$
由于$$v_x > 0$$,船会向东偏移,即选项 A。
5. 物体处于静止状态,三个力的矢量和为零:
$$F_3 = -(F_1 + F_2) = -((1, 2) + (-1, -3)) = (0, 1)$$
即选项 A。
6. 由平衡条件,$$F_2 = -(F_1 + F_3)$$。计算$$F_1 + F_3$$:
$$F_1 + F_3$$的大小为$$\sqrt{1^2 + 2^2 + 2 \times 1 \times 2 \times \cos 60^\circ} = \sqrt{7} \, \text{N}$$
因此$$F_2$$的大小为$$\sqrt{7} \, \text{N}$$,即选项 C。
7. 设$$F_1 = F_2 = F$$,当夹角为$$90^\circ$$时,合力为$$F\sqrt{2} = 20 \, \text{N}$$,解得$$F = 10\sqrt{2} \, \text{N}$$。
当夹角为$$120^\circ$$时,合力为$$F = 10\sqrt{2} \, \text{N}$$,即选项 B。
8. 建立坐标系,设$$A$$为原点,$$B$$的坐标为$$(500, -500\sqrt{3})$$,$$C$$的坐标为$$(-1000\sqrt{3}, -1000)$$。
$$BC$$的距离为$$\sqrt{(500 + 1000\sqrt{3})^2 + (-500\sqrt{3} + 1000)^2} = 1000 \, \text{km}$$,即选项 C。
9. 设$$OA$$和$$OB$$的夹角为$$\theta$$,由平衡条件:
$$4 \cos \frac{\theta}{2} + 4 \cos \frac{\theta}{2} = 4\sqrt{3}$$
解得$$\cos \frac{\theta}{2} = \frac{\sqrt{3}}{2}$$,即$$\theta = \frac{\pi}{3}$$,选项 C。
10. 由平衡条件,$$F_3 = -(F_1 + F_2)$$。计算$$F_1 + F_2$$的大小:
$$|F_1 + F_2| = \sqrt{2^2 + 4^2 + 2 \times 2 \times 4 \times \cos 60^\circ} = 2\sqrt{7}$$
因此$$F_3$$的大小为$$2\sqrt{7}$$,即选项 D。
.jpg)