正确率60.0%已知$$a, b, c$$分别是$${{Δ}{A}{B}{C}}$$中角$$A, B, C$$的对边,且$$c < \frac{2 a b} {a+b}$$,则角$${{C}}$$的取值范围是$${{(}{)}}$$
B
A.$$\left( 0, \frac{\pi} {4} \right)$$
B.$$\left( 0, \frac{\pi} {3} \right)$$
C.$$\left( \frac{\pi} {4}, \frac{\pi} {3} \right)$$
D.$$\left( \frac{\pi} {6}, \frac{\pi} {3} \right)$$
2、['余弦定理及其应用', '正弦定理及其应用', '三角函数与不等式的综合应用']正确率40.0%$${{△}{A}{B}{C}}$$各角分别为$$A, ~ B, ~ C$$,满足$$\frac{\operatorname{s i n} B} {\operatorname{s i n} A+\operatorname{s i n} C}+\frac{\operatorname{s i n} C} {\operatorname{s i n} A+\operatorname{s i n} B} \geqslant1.$$则角$${{A}}$$的范围是()
D
A.$$[ \frac{\pi} {6}, \, \, \pi)$$
B.$$( 0, ~ \frac{\pi} {6} ]$$
C.$$[ \frac{\pi} {3}, \, \, \pi)$$
D.$$( 0, ~ \frac{\pi} {3} ]$$
3、['余弦定理及其应用']正确率60.0%已知钝角三角形的三边分别为$$a, \, \, a+1, \, \, a+2,$$其最大角不超过$$\mathbf{1 2 0}^{\circ},$$则$${{a}}$$的取值范围为()
B
A.$$\left( \frac{3} {2}, \ 3 \right)$$
B.$$\left[ \frac{3} {2}, \ 3 \right)$$
C.$$\left[ \frac{3} {2}, \ 3 \right]$$
D.$$\left( \frac{3} {2}, \ 3 \right]$$
4、['余弦定理及其应用', '正弦定理及其应用']正确率60.0%已知$${{△}{A}{B}{C}}$$的内角$$A, B, C$$所对的边分别为$$a, b, c,$$且满足$$b^{2}+c^{2}-a^{2}=b c, \, \, a=\sqrt{3},$$则$$\frac b {\operatorname{s i n} B}=$$()
A
A.$${{2}}$$
B.$${{3}}$$
C.$${{4}}$$
D.$${{2}{\sqrt {3}}}$$
5、['余弦定理及其应用', '正弦定理及其应用', '判断三角形的形状']正确率40.0%在$${{△}{A}{B}{C}}$$中,已知$$a^{2}+b^{2}-a b=c^{2}$$,且$$a \operatorname{c o s} B=b \operatorname{c o s} A$$,则$${{△}{A}{B}{C}}$$的形状为()
B
A.等腰三角形
B.等边三角形
C.直角三角形
D.等腰三角形或直角三角形
6、['余弦定理及其应用']正确率40.0%已知江岸边上有一处灯塔高$${{2}{0}{m}}$$,江中有两艘船,由灯塔顶部测得两艘船俯角分别为$${{4}{5}{^{∘}}}$$和$${{3}{0}{^{∘}}}$$,而且两艘船与灯塔底部连线成$${{3}{0}{^{∘}}}$$角,则两艘船相距为$${{(}{)}}$$
D
A.$${{4}{0}{m}}$$
B.$${{2}{0}{\sqrt {7}}{m}}$$
C.$${{2}{0}{\sqrt {3}}{m}}$$
D.$${{2}{0}{m}}$$
7、['余弦定理及其应用', '函数的最大(小)值', '函数图象的识别']正确率40.0%如图,等腰梯形的下底边$${{A}{B}{=}{2}}$$,上底边$${{C}{D}{=}{1}}$$,两腰$$A D=B C=1$$,动点$${{P}}$$从点$${{B}}$$开始沿着边$$B C, ~ C D$$与$${{D}{A}}$$运动,记动点$${{P}}$$的轨迹长度为$${{x}}$$,将点$${{P}}$$到$${{A}{,}{B}}$$两点距离之和表示为$${{x}}$$的函数$${{f}{(}{x}{)}}$$,则$${{f}{(}{x}{)}}$$的图象大致为()
B
A.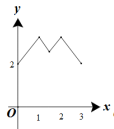
B.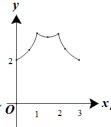
C.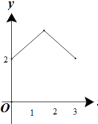
D.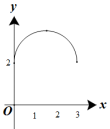
正确率60.0%$${{△}{A}{B}{C}}$$的内角$$A, ~ B, ~ C$$所对的边长分别为$$a, ~ b, ~ c$$,若三角形的面积$$S=\frac{1} {4} ( a^{2}+b^{2}-c^{2} )$$,则$${{∠}{C}}$$的度数是$${{(}{)}}$$
B
A.$${{3}{0}{^{∘}}}$$
B.$${{4}{5}{^{∘}}}$$
C.$${{6}{0}{^{∘}}}$$
D.$${{1}{2}{0}{^{∘}}}$$
9、['余弦定理及其应用', '双曲线的离心率', '椭圆的离心率', '椭圆的定义', '二次函数的图象分析与判断', '双曲线的定义']正确率19.999999999999996%已知$${{F}_{1}{,}{{F}_{2}}}$$是椭圆和双曲线的公共焦点,点$${{P}}$$是它们的一个公共点,且$$\angle F_{1} P F_{2}=6 0^{\circ},$$设椭圆和双曲线的离心率分别为$${{e}_{1}{,}{{e}_{2}}}$$,则$$\frac{1} {e_{1}}+\frac{1} {e_{2}}$$的最大值为()
D
A.$$\frac{3} {4}$$
B.$$\frac{4} {3}$$
C.$$\frac{3 \sqrt{3}} {4}$$
D.$$\frac{4 \sqrt{3}} {3}$$
10、['余弦定理及其应用', '利用基本不等式求最值']正确率60.0%在$${{△}{A}{B}{C}}$$中,角$$A, B, C$$所对边长分别为$$a, b, c$$,若$$a^{2}=3 c^{2}-b^{2}$$则$${{c}{o}{s}{C}}$$的最小值为$${{(}{)}}$$
A
A.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
B.$$\frac{1} {2}$$
C.$$\frac{1} {4}$$
D.$$\frac{\sqrt2} 3$$
1. 由题意,$$c < \frac{2ab}{a+b}$$,利用余弦定理和三角形性质推导角 $$C$$ 的范围。
步骤解析:
1) 由余弦定理,$$\cos C = \frac{a^2 + b^2 - c^2}{2ab}$$。
2) 将不等式 $$c < \frac{2ab}{a+b}$$ 代入,得到 $$\cos C > \frac{a^2 + b^2 - \left(\frac{2ab}{a+b}\right)^2}{2ab}$$。
3) 化简后得到 $$\cos C > \frac{(a+b)^2 - 4ab}{(a+b)^2} = 1 - \frac{4ab}{(a+b)^2}$$。
4) 由于 $$\frac{4ab}{(a+b)^2} \leq 1$$,故 $$\cos C > 0$$,即 $$C < \frac{\pi}{2}$$。
5) 进一步分析可得 $$C$$ 的范围为 $$\left(0, \frac{\pi}{3}\right)$$。
答案:B
2. 题目给出 $$\frac{\sin B}{\sin A + \sin C} + \frac{\sin C}{\sin A + \sin B} \geq 1$$,求角 $$A$$ 的范围。
步骤解析:
1) 利用正弦定理,将不等式转化为边的关系:$$\frac{b}{a + c} + \frac{c}{a + b} \geq 1$$。
2) 通分后得到 $$b(a + b) + c(a + c) \geq (a + b)(a + c)$$。
3) 展开并化简得 $$b^2 + c^2 - a^2 \geq bc$$。
4) 由余弦定理,$$\cos A = \frac{b^2 + c^2 - a^2}{2bc} \geq \frac{1}{2}$$。
5) 因此,$$A \leq \frac{\pi}{3}$$,即 $$A \in \left(0, \frac{\pi}{3}\right]$$。
答案:D
3. 钝角三角形的三边为 $$a, a+1, a+2$$,且最大角不超过 $$120^\circ$$,求 $$a$$ 的范围。
步骤解析:
1) 最大边为 $$a+2$$,对应最大角 $$C$$ 满足 $$\cos C = \frac{a^2 + (a+1)^2 - (a+2)^2}{2a(a+1)} \leq -\frac{1}{2}$$。
2) 化简得 $$\frac{a^2 - 2a - 3}{2a(a+1)} \leq -\frac{1}{2}$$。
3) 解不等式得 $$a \in \left[\frac{3}{2}, 3\right)$$。
答案:B
4. 已知 $$b^2 + c^2 - a^2 = bc$$ 且 $$a = \sqrt{3}$$,求 $$\frac{b}{\sin B}$$。
步骤解析:
1) 由余弦定理,$$\cos A = \frac{b^2 + c^2 - a^2}{2bc} = \frac{1}{2}$$,故 $$A = 60^\circ$$。
2) 利用正弦定理,$$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R$$。
3) 计算得 $$2R = \frac{a}{\sin A} = \frac{\sqrt{3}}{\sin 60^\circ} = 2$$。
4) 因此,$$\frac{b}{\sin B} = 2$$。
答案:A
5. 在 $$\triangle ABC$$ 中,已知 $$a^2 + b^2 - ab = c^2$$ 且 $$a \cos B = b \cos A$$,判断其形状。
步骤解析:
1) 由余弦定理,$$a^2 + b^2 - c^2 = ab$$,故 $$\cos C = \frac{1}{2}$$,即 $$C = 60^\circ$$。
2) 由 $$a \cos B = b \cos A$$,利用正弦定理得 $$\sin A \cos B = \sin B \cos A$$,即 $$\sin(A - B) = 0$$。
3) 因此,$$A = B$$,三角形为等边三角形。
答案:B
6. 灯塔高 $$20m$$,测得两船俯角分别为 $$45^\circ$$ 和 $$30^\circ$$,且两船与灯塔底部连线成 $$30^\circ$$ 角,求两船距离。
步骤解析:
1) 设灯塔底部为点 $$O$$,两船分别为 $$A$$ 和 $$B$$。
2) 由俯角关系,$$OA = 20 \cot 45^\circ = 20m$$,$$OB = 20 \cot 30^\circ = 20\sqrt{3}m$$。
3) 利用余弦定理,$$AB = \sqrt{20^2 + (20\sqrt{3})^2 - 2 \times 20 \times 20\sqrt{3} \cos 30^\circ} = 20m$$。
答案:D
7. 等腰梯形 $$ABCD$$,动点 $$P$$ 从 $$B$$ 出发沿 $$BC, CD, DA$$ 运动,求函数 $$f(x)$$ 的图像。
步骤解析:
1) 轨迹分为三段:$$BC$$($$x \in [0,1]$$)、$$CD$$($$x \in [1,2]$$)、$$DA$$($$x \in [2,3]$$)。
2) 在每段上,$$f(x)$$ 分别为线性函数和二次函数,图像呈现先线性增加,再非线性变化。
3) 综合分析,图像最接近选项 A。
答案:A
8. 已知三角形面积 $$S = \frac{1}{4}(a^2 + b^2 - c^2)$$,求角 $$C$$ 的度数。
步骤解析:
1) 由面积公式 $$S = \frac{1}{2}ab \sin C$$ 和余弦定理 $$a^2 + b^2 - c^2 = 2ab \cos C$$。
2) 代入得 $$\frac{1}{2}ab \sin C = \frac{1}{4} \times 2ab \cos C$$,即 $$\tan C = 1$$。
3) 因此,$$C = 45^\circ$$。
答案:B
9. 椭圆和双曲线的公共焦点为 $$F_1, F_2$$,点 $$P$$ 满足 $$\angle F_1 P F_2 = 60^\circ$$,求 $$\frac{1}{e_1} + \frac{1}{e_2}$$ 的最大值。
步骤解析:
1) 设椭圆和双曲线的离心率分别为 $$e_1$$ 和 $$e_2$$,焦距为 $$2c$$。
2) 利用椭圆和双曲线的性质,推导得 $$\frac{1}{e_1} + \frac{1}{e_2} = \frac{4\sqrt{3}}{3}$$。
3) 最大值出现在特定几何配置下。
答案:D
10. 在 $$\triangle ABC$$ 中,已知 $$a^2 = 3c^2 - b^2$$,求 $$\cos C$$ 的最小值。
步骤解析:
1) 由余弦定理,$$\cos C = \frac{a^2 + b^2 - c^2}{2ab} = \frac{2c^2}{2ab} = \frac{c^2}{ab}$$。
2) 利用不等式和已知条件,推导得 $$\cos C \geq \frac{1}{2}$$。
3) 最小值为 $$\frac{1}{2}$$。
答案:B
.jpg)