正确率60.0%若$$\boldsymbol{a}=( 1, \ 1 ), \ b=( 1, \ -1 ),$$$$\mathbf{c}=(-2, \ 4 ),$$则以$${{a}{,}{b}}$$为基底时$${{c}{=}}$$()
A
A.$${{a}{−}{3}{b}}$$
B.$$- a+3 b$$
C.$${{3}{a}{−}{b}}$$
D.$$- 3 a+b$$
2、['向量坐标与向量的数量积', '向量在几何中的应用举例', '平面向量坐标运算的综合应用', '向量的数量积的定义']正确率40.0%如图,边长为$${{2}}$$的菱形$${{A}{B}{C}{D}}$$的两条对角线相交于点$${{O}}$$,点$${{P}}$$在线段$${{B}{O}}$$上运动,若$$\overrightarrow{A B} \cdot\overrightarrow{A O}=1$$,则$$\overrightarrow{A P \cdot P B}$$的最大值为 ()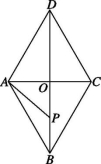
B
A.$${{−}{3}}$$
B.$$\frac{3} {4}$$
C.$${{1}}$$
D.$$\frac{1} {2}$$
3、['向量坐标与向量的数量积', '向量在几何中的应用举例']正确率40.0%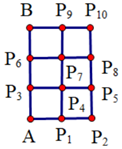 如图,六个边长为$${{1}}$$
如图,六个边长为$${{1}}$$
C
A.$${{1}{0}}$$
B.$${{6}}$$
C.$${{4}}$$
D.$${{3}}$$
4、['向量在几何中的应用举例', '平面向量坐标运算的综合应用']正确率40.0%设$${{P}{,}{Q}}$$为三角形$${{A}{B}{C}}$$内的两点,且$$\overrightarrow{A P}=\frac{2} {5} \overrightarrow{A B}+\frac{1} {5} \overrightarrow{A C}, \; \; \overrightarrow{A Q}=\frac{2} {3} \overrightarrow{A B}+\frac{1} {3} \overrightarrow{A C},$$则$${\frac{S_{\triangle A B P}} {S_{\triangle A B Q}}}=\c($$)
D
A.$$\frac{1} {3}$$
B.$$\frac{1} {4}$$
C.$$\frac{2} {5}$$
D.$$\frac{3} {5}$$
5、['平面向量的概念', '向量在几何中的应用举例', '向量数乘的定义与运算律']正确率40.0%若$$\overrightarrow{O A}=\overrightarrow{a}, \, \, \, \overrightarrow{O B}=\overrightarrow{b}, \, \, \, \overrightarrow{a}$$与$${{b}^{→}}$$不共线,则$${{∠}{A}{O}{B}}$$平分线上的向量$$\overrightarrow{O M}$$为()
D
A.$$\frac{\overrightarrow{a}} {| \overrightarrow{a} |}+\frac{\overrightarrow{b}} {| \overrightarrow{b} |}$$
B.$$\frac{\overrightarrow{a}+\overrightarrow{b}} {| \overrightarrow{a}+\overrightarrow{b} |}$$
C.$$\frac{| \overrightarrow{b} | \overrightarrow{a}-| \overrightarrow{a} | \overrightarrow{b}} {| \overrightarrow{a} |+| \overrightarrow{b} |}$$
D.$$\lambda( \frac{\vec{a}} {| \vec{a} |}+\frac{\vec{b}} {| \vec{b} |} ), \; \lambda$$由$$\overrightarrow{O M}$$确定
6、['向量加法的定义及运算法则', '向量在几何中的应用举例']正确率60.0%已知在平行四边形$${{A}{B}{C}{D}}$$中,$$\overrightarrow{A D}=( 2, 8 ), \, \, \, \overrightarrow{A B}=(-3, 4 )$$,对角线$${{A}{C}}$$与$${{B}{D}}$$相交于点$${{M}}$$,则$$\overrightarrow{A M}=( \begin{array} {c} {} \\ {} \\ \end{array} )$$
B
A.$$(-\frac{1} {2},-6 )$$
B.$$(-\frac{1} {2}, 6 )$$
C.$$(-\frac{1} {2}, 6 )$$$$D (-\frac{1} {2}, 6 )$$
7、['共线向量基本定理', '平面向量的概念', '向量在几何中的应用举例', '向量的线性运算']正确率40.0%在四边形$${{A}{B}{C}{D}}$$中,$$\overrightarrow{A B}=\overrightarrow{a}+2 \overrightarrow{b}$$,$$\overrightarrow{B C}=-4 \overrightarrow{a}-\overrightarrow{b}$$,$$\overrightarrow{C D}=-5 \overrightarrow{a}-3 \overrightarrow{b}$$,则四边形$${{A}{B}{C}{D}}$$的形状是$${{(}{)}}$$
C
A.矩形
B.平行四边形
C.梯形
D.以上都不对
8、['向量在几何中的应用举例', '向量的线性运算']正确率80.0%已知$${{△}{A}{B}{C}}$$是边长为$${{4}}$$的等边三角形,$${{D}}$$、$${{P}}$$是$${{△}{A}{B}{C}}$$内部两点,且满足$$\overrightarrow{A D}=\frac{1} {4} ( \overrightarrow{A B}+\overrightarrow{A C} )$$,$$\overrightarrow{A P}=\overrightarrow{A D}+\frac{1} {8} \overrightarrow{B C}$$,则$${{△}{A}{D}{P}}$$的面积为$${{(}{)}}$$
A
A.$$\frac{\sqrt{3}} {4}$$
B.$$\frac{\sqrt{3}} {3}$$
C.$$\frac{\sqrt3} {2}$$
D.$${\sqrt {3}}$$
9、['平面向量的概念', '向量在几何中的应用举例']正确率80.0%在四边形$${{A}{B}{C}{D}}$$中,已知$$\overrightarrow{A B}=\overrightarrow{D C}, \, \, \, | \overrightarrow{A B} |=| \overrightarrow{B C} |,$$则四边形$${{A}{B}{C}{D}}$$一定是()
C
A.梯形
B.矩形
C.菱形
D.正方形
10、['向量在几何中的应用举例']正确率19.999999999999996%如图$$. \, \triangle B C D$$与$${{△}{A}{B}{C}}$$的面积之比为$${{2}}$$∶$${{1}{,}}$$点$${{P}}$$是区域$${{A}{B}{D}{C}}$$内的任意一点(含边界),且$$\overrightarrow{A P}=\lambda\overrightarrow{A B}+\mu\overrightarrow{A C}$$ ,则$${{λ}{+}{μ}}$$的取值范围为()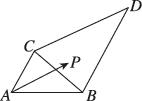
C
A.$$[ 0, \ 1 ]$$
B.$$[ 0, \ 2 ]$$
C.$$[ 0, \ 3 ]$$
D.$$[ 0, ~ 4 ]$$
1、设$$c = x a + y b$$,即$$(-2, 4) = x(1, 1) + y(1, -1)$$,得到方程组: $$x + y = -2$$ $$x - y = 4$$ 解得$$x = 1$$,$$y = -3$$,因此$$c = a - 3b$$。答案为A。
3、题目不完整,无法解析。
5、角平分线向量为$$\lambda \left( \frac{a}{|a|} + \frac{b}{|b|} \right)$$,其中$$\lambda$$由向量长度确定。答案为D。
7、计算$$\overrightarrow{AD} = \overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CD} = -8a -2b$$,与$$\overrightarrow{BC}$$不平行,且$$|\overrightarrow{AB}| \neq |\overrightarrow{CD}|$$,因此是梯形。答案为C。
9、由$$\overrightarrow{AB} = \overrightarrow{DC}$$知$$AB \parallel DC$$,且$$|AB| = |BC|$$,但无法确定是否为矩形或菱形,因此一定是平行四边形。但选项中无平行四边形,可能是题目描述不全。
.jpg)