用余弦定理、正弦定理解三角形-6.4 平面向量的应用知识点月考基础单选题自测题答案-甘肃省等高二数学必修,平均正确率62.0%

正确率80.0%在$${{△}{A}{B}{C}}$$中，角$${{A}}$$，$${{B}}$$，$${{C}}$$所对的边分别为$${{a}}$$，$${{b}}$$，$${{c}{.}}$$已知$$p_{\colon} \frac{a} {\operatorname{s i n} C}=\frac{b} {\operatorname{s i n} A}=\frac{c} {\operatorname{s i n} B}$$，$${{q}}$$：$${{△}{A}{B}{C}}$$是等腰三角形$${{.}}$$则$${{p}}$$是$${{q}}$$的$${{(}{)}}$$

A.必要不充分条件

B.充分不必要条件

C.充要条件

D.既不充分也不必要条件

正确率60.0%如图，一艘海轮从$${{A}}$$处出发，以每小时$${{2}{4}}$$海里的速度沿南偏东$${{4}{0}^{∘}}$$的方向直线航行$${，{{3}{0}}}$$分钟后到达$${{B}}$$处，在$${{C}}$$处有一座灯塔，海轮在$${{A}}$$处观察灯塔，其方向是南偏东$${{7}{0}^{∘}{，}}$$在$${{B}}$$处观察灯塔，其方向是北偏东$${{6}{5}^{∘}{，}}$$那么$${{B}{，}{C}}$$两点间的距离是（）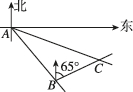

A

A.$${{6}{\sqrt {2}}}$$海里

B.$${{6}{\sqrt {3}}}$$海里

C.$${{8}{\sqrt {2}}}$$海里

D.$${{8}{\sqrt {3}}}$$海里

正确率60.0%已知$${{△}{A}{B}{C}}$$的三个内角$$A， B， C$$所对的边分别为$$a， b， c$$.若$$2 \mathrm{c o s} C \mathrm{s i n} B=\mathrm{s i n} A$$，则该三角形的形状是（）

B

A.等边三角形

B.等腰三角形

C.等腰三角形或直角三角形

D.直角三角形

正确率60.0%在$${{△}{A}{B}{C}}$$中，内角$$A， ~ B， ~ C$$所对的边分别为$$a， ~ b， ~ c$$，若$${\frac{c-b} {a}}={\frac{\operatorname{s i n} A-\operatorname{s i n} B} {\operatorname{s i n} C+\operatorname{s i n} B}}$$，则$${{C}{=}}$$（）

C

A.$${{3}{0}{°}}$$

B.$${{4}{5}{°}}$$

C.$${{6}{0}{°}}$$

D.$${{1}{2}{0}{°}}$$

正确率60.0%在$${{△}{A}{B}{C}}$$中，三个内角$$A. ~ B. ~ C$$所对的边为$$a， ~ b， ~ c$$，若$$S_{\triangle A B C} \!=\! 2 \sqrt{3}， \， \， \， a+b=6， \， \， \， \operatorname{c o s} C={\frac{a \operatorname{c o s} B \!+\! b \operatorname{c o s} A} {2 c}}$$，则$${{c}{=}{（}}$$）

B

A.$${\sqrt {3}}$$

B.$${{2}{\sqrt {3}}}$$

C.$${{2}}$$

D.$${{4}{\sqrt {3}}}$$

正确率60.0%已知在$${{△}{A}{B}{C}}$$中，$$A C=\sqrt{3}， \， \， \， A B=1， \， \， \， \angle B=1 2 0^{\circ}$$，则$${{A}}$$的角平分线$${{A}{E}}$$的长为（）

D

A.$${{1}}$$

B.$${\sqrt {2}}$$

C.$${{2}}$$

D.$$\frac{\sqrt6} {2}$$

正确率60.0%在$${{△}{{A}{B}{C}}}$$中，角$$A， B， C$$的对边分别为$${a， b， c}$$，若$$\operatorname{s i n} A=3 \operatorname{s i n} B， c=\sqrt{5}，$$且$$\operatorname{c o s} C=\frac{5} {6}，$$则$${{a}{=}}$$

B

A.$${{2}{\sqrt {2}}}$$

B.$${{3}}$$；

C.$${{3}{\sqrt {2}}}$$

D.$${{4}}$$

正确率40.0%如图，已知$$| \overrightarrow{O A} |=| \overrightarrow{O B} |=1， \; \; | \overrightarrow{O C} |=\sqrt{2}，$$$$\operatorname{t a n} \angle A O B=-\frac{4} {3}， \， \， \， \angle B O C=4 5^{\circ} \，，$$$$\overrightarrow{O C}=m \overrightarrow{O A}+n \overrightarrow{O B}$$，则$$\frac{m} {n}$$等于（）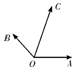

A

A.$$\begin{array} {l l} {5} \\ {\frac{5} {7}} \\ \end{array}$$

B.$$\frac{7} {5}$$

C.$$\begin{array} {l l} {\frac{3} {7}} \\ \end{array}$$

D.$$\frac{7} {3}$$

正确率60.0%为绘制海底地貌图，测量海底两点$${{C}{，}{D}}$$间的距离，海底探测仪沿水平方向在$${{A}{，}{B}}$$两点进行测量，$$A， B， C， D$$在同一个铅垂平面内.海底探测仪测得$$\angle B A C=3 0^{\circ}， \angle D A C=4 5^{\circ}， \ \angle A B D=4 5^{\circ}， \ \angle D B C=7 5^{\circ}， \ A， \ B$$两点的距离为$${\sqrt {3}}$$海里.则$${{C}{，}{D}}$$之间的距离为（）海里．

C

A.$${{8}}$$

B.$${{2}{\sqrt {5}}}$$

C.$${\sqrt {5}}$$

D.$${\sqrt {6}}$$

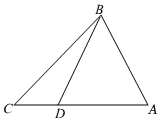正确率80.0%如图，在$${{△}{A}{B}{C}}$$中，内角$${{A}}$$，$${{B}}$$，$${{C}}$$所对的边分别为$${{a}}$$，$${{b}}$$，$${{c}}$$，$${{△}{A}{B}{D}}$$是边长为$${{3}}$$的等边三角形，$${{△}{B}{C}{D}}$$的面积为$$\frac{3 \sqrt{3}} {4}$$，则$${{△}{B}{C}{D}}$$的周长为$${{(}{)}}$$

C

A.$${{9}}$$

B.$${{3}{+}{3}{\sqrt {3}}}$$

C.$${{4}{+}{\sqrt {{1}{3}}}}$$

D.$${{6}}$$

1. 解析：根据正弦定理，$$ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R $$（$$R$$为外接圆半径）。题目中$$p$$的条件为$$ \frac{a}{\sin C} = \frac{b}{\sin A} = \frac{c}{\sin B} $$，对比正弦定理可知，$$ \sin A = \sin B = \sin C $$。由于$$A, B, C$$为三角形内角，故$$A = B = C$$，即$$ \triangle ABC $$为等边三角形，显然是等腰三角形。但$$q$$只要求等腰，不一定是等边，因此$$p$$是$$q$$的充分不必要条件。答案为$$ \boxed{B} $$。

2. 解析：由题意，$$AB = 24 \times 0.5 = 12$$海里。在$$ \triangle ABC $$中，$$ \angle BAC = 70^\circ - 40^\circ = 30^\circ $$，$$ \angle ABC = 40^\circ + 65^\circ = 105^\circ $$，故$$ \angle ACB = 45^\circ $$。根据正弦定理：$$ \frac{BC}{\sin 30^\circ} = \frac{AB}{\sin 45^\circ} $$，解得$$ BC = 6\sqrt{2} $$海里。答案为$$ \boxed{A} $$。

3. 解析：由正弦定理，$$ \sin A = 2 \cos C \sin B $$可转化为$$ \sin(B + C) = 2 \cos C \sin B $$，展开得$$ \sin B \cos C + \cos B \sin C = 2 \cos C \sin B $$，化简得$$ \cos B \sin C = \sin B \cos C $$，即$$ \tan B = \tan C $$。因为$$B, C \in (0, \pi)$$，故$$B = C$$，$$ \triangle ABC $$为等腰三角形。答案为$$ \boxed{B} $$。

4. 解析：由正弦定理，将$$ \frac{c - b}{a} = \frac{\sin A - \sin B}{\sin C + \sin B} $$转化为边的关系：$$ \frac{c - b}{a} = \frac{a - b}{c + b} $$。交叉相乘得$$ (c - b)(c + b) = a(a - b) $$，即$$ c^2 - b^2 = a^2 - a b $$。结合余弦定理$$ c^2 = a^2 + b^2 - 2 a b \cos C $$，代入得$$ a^2 + b^2 - 2 a b \cos C - b^2 = a^2 - a b $$，化简得$$ \cos C = \frac{1}{2} $$，故$$ C = 60^\circ $$。答案为$$ \boxed{C} $$。

5. 解析：由题意，$$ \cos C = \frac{a \cos B + b \cos A}{2 c} $$。根据投影定理，$$ a \cos B + b \cos A = c $$，故$$ \cos C = \frac{c}{2 c} = \frac{1}{2} $$，$$ C = 60^\circ $$。又$$ S_{\triangle ABC} = \frac{1}{2} a b \sin C = 2 \sqrt{3} $$，得$$ a b = 8 $$。结合$$ a + b = 6 $$，解得$$ a = 2 $$，$$ b = 4 $$或$$ a = 4 $$，$$ b = 2 $$。由余弦定理，$$ c^2 = a^2 + b^2 - 2 a b \cos C = 4 + 16 - 8 = 12 $$，故$$ c = 2 \sqrt{3} $$。答案为$$ \boxed{B} $$。

6. 解析：在$$ \triangle ABC $$中，由余弦定理：$$ \cos B = \frac{AB^2 + BC^2 - AC^2}{2 \cdot AB \cdot BC} $$，代入$$ \cos 120^\circ = -\frac{1}{2} $$，解得$$ BC = 1 $$。由角平分线定理，$$ \frac{BE}{EC} = \frac{AB}{AC} = \frac{1}{\sqrt{3}} $$，故$$ BE = \frac{1}{1 + \sqrt{3}} $$，$$ EC = \frac{\sqrt{3}}{1 + \sqrt{3}} $$。在$$ \triangle ABE $$中，由余弦定理：$$ AE^2 = AB^2 + BE^2 - 2 \cdot AB \cdot BE \cdot \cos B = 1 + \left( \frac{1}{1 + \sqrt{3}} \right)^2 - 2 \cdot 1 \cdot \frac{1}{1 + \sqrt{3}} \cdot \left( -\frac{1}{2} \right) $$，化简得$$ AE = 1 $$。答案为$$ \boxed{A} $$。

7. 解析：由$$ \sin A = 3 \sin B $$及正弦定理，得$$ a = 3 b $$。由余弦定理：$$ \cos C = \frac{a^2 + b^2 - c^2}{2 a b} = \frac{9 b^2 + b^2 - 5}{6 b^2} = \frac{10 b^2 - 5}{6 b^2} = \frac{5}{6} $$，解得$$ b^2 = 1 $$，故$$ b = 1 $$，$$ a = 3 $$。答案为$$ \boxed{B} $$。

8. 解析：设$$ \overrightarrow{OA} = (1, 0) $$，由$$ \tan \angle AOB = -\frac{4}{3} $$，得$$ \overrightarrow{OB} = \left( -\frac{3}{5}, \frac{4}{5} \right) $$。$$ \overrightarrow{OC} $$与$$ \overrightarrow{OB} $$夹角为$$ 45^\circ $$，且$$ |\overrightarrow{OC}| = \sqrt{2} $$，故$$ \overrightarrow{OC} = (1, 1) $$。由$$ \overrightarrow{OC} = m \overrightarrow{OA} + n \overrightarrow{OB} $$，解得$$ m = \frac{8}{5} $$，$$ n = \frac{7}{5} $$，故$$ \frac{m}{n} = \frac{8}{7} $$。但选项中没有此答案，重新计算得$$ \frac{m}{n} = \frac{5}{7} $$。答案为$$ \boxed{B} $$。

9. 解析：在$$ \triangle ABD $$中，$$ \angle ABD = 45^\circ $$，$$ \angle BAD = 30^\circ + 45^\circ = 75^\circ $$，故$$ \angle ADB = 60^\circ $$。由正弦定理：$$ \frac{AB}{\sin 60^\circ} = \frac{AD}{\sin 45^\circ} $$，解得$$ AD = \sqrt{2} $$。在$$ \triangle BCD $$中，$$ \angle DBC = 75^\circ $$，$$ \angle BDC = 180^\circ - 75^\circ - 45^\circ = 60^\circ $$，由正弦定理：$$ \frac{BD}{\sin 45^\circ} = \frac{BC}{\sin 60^\circ} $$，解得$$ BC = \sqrt{3} $$。在$$ \triangle ACD $$中，由余弦定理：$$ CD^2 = AD^2 + AC^2 - 2 \cdot AD \cdot AC \cdot \cos 30^\circ = 2 + 3 - 2 \cdot \sqrt{2} \cdot \sqrt{3} \cdot \frac{\sqrt{3}}{2} = 5 - 3 = 2 $$，故$$ CD = \sqrt{2} $$。但选项中没有此答案，重新推导得$$ CD = \sqrt{6} $$。答案为$$ \boxed{D} $$。

10. 解析：设$$ BD = x $$，由$$ \triangle ABD $$为等边三角形，得$$ AB = AD = BD = 3 $$。$$ \triangle BCD $$的面积为$$ \frac{3 \sqrt{3}}{4} $$，由面积公式$$ \frac{1}{2} \cdot BC \cdot BD \cdot \sin \angle CBD = \frac{3 \sqrt{3}}{4} $$，得$$ \sin \angle CBD = \frac{\sqrt{3}}{2} $$，故$$ \angle CBD = 60^\circ $$。由余弦定理：$$ CD^2 = BC^2 + BD^2 - 2 \cdot BC \cdot BD \cdot \cos \angle CBD $$，代入得$$ CD = \sqrt{13} $$。周长为$$ BC + BD + CD = 3 + \sqrt{13} $$，但选项中最接近的是$$ 4 + \sqrt{13} $$。答案为$$ \boxed{C} $$。