正确率60.0%如果一个物体受到力的作用,并在力的方向上发生了一段位移,我们就说这个力对物体做了功,功的计算公式为$$W=\boldsymbol{F} \cdot\boldsymbol{S}$$(其中$${{W}}$$是功$${,{F}}$$是力$${,{S}}$$是位移).一物体在力$$\boldsymbol{F}_{1}=( 2, \ 4 )$$和$$\boldsymbol{F}_{2}=(-5, \ 3 )$$的作用下,由点$$A ( 1, \ 0 )$$移动到点$$B ( 2, ~ 4 ),$$在这个过程中这两个力的合力对物体所做的功为()
A
A.$${{2}{5}}$$
B.$${{5}}$$
C.$${{−}{5}}$$
D.$${{−}{{2}{5}}}$$
2、['向量在物理中的应用举例']正确率80.0%已知力$$\overrightarrow{F}=( 5, 2 )$$作用于一物体,使物体从点$$A (-1, 3 )$$处移动到点$$B ( 2, 6 )$$处,则力$${{F}}$$对物体所做的功为$${{(}{)}}$$
A.$${{9}}$$
B.$${{−}{9}}$$
C.$${{2}{1}}$$
D.$${{−}{{2}{1}}}$$
3、['向量的数量积', '向量在物理中的应用举例', '向量的夹角']正确率80.0%若平面上的三个力$$\overrightarrow{F_{1}}$$,$$\overrightarrow{F_{2}}$$,$$\overrightarrow{F_{3}}$$作用于一点,且处于平衡状态$${{.}}$$已知$$| \overrightarrow{F_{1}} |=1 N$$,$$| \overrightarrow{F_{3}} |=2 N$$,$$\overrightarrow{F_{1}}$$与$$\overrightarrow{F_{3}}$$的夹角为$${{6}{0}{°}}$$,则$$\overrightarrow{F_{2}}$$的大小为$${{(}{)}}$$
A.$${{1}{N}}$$
B.$${\sqrt {3}{N}}$$
C.$${\sqrt {7}{N}}$$
D.$${{3}{N}}$$
4、['向量在物理中的应用举例']正确率60.0%如图为某种礼物降落伞的示意图,其中有$${{8}}$$根绳子和伞面连接,每根绳子和水平面的法向量的夹角均为$${{6}{0}^{∘}}$$.已知礼物的质量为$${{1}{k}{g}{,}}$$每根绳子的拉力大小相同.若重力加速度$${{g}}$$取$$9. 8 ~ \mathrm{m / s^{2}},$$则降落伞在匀速下落的过程中每根绳子拉力的大小为()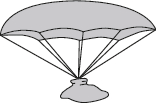
B
A.$$2. 2 5 ~ \mathrm{N}$$
B.$$2. 4 5 ~ \mathrm{N}$$
C.$${{2}{.}{5}{N}}$$
D.$$\mathrm{2. 7 5 ~ N}$$
5、['向量在物理中的应用举例']正确率60.0%长江某地南北两岸平行,一艘游船从南岸码头$${{A}}$$出发航行到北岸,假设游船在静水中的航行速度$${{{v}_{1}}^{→}}$$的大小为$$| \vec{v_{1}} |=1 4 ~ \mathrm{k m} / \mathrm{h}$$,水流的速度$${{{v}_{2}}^{→}}$$的大小为$$| \overrightarrow{v_{2}} |=4 ~ \mathrm{k m} / \mathrm{h}$$.设$${{{v}_{1}}^{→}}$$和$${{{v}_{2}}^{→}}$$的夹角为$$\theta\; ( \; 0^{\circ} \; < \; \theta\; < \; 1 8 0^{\circ} ) \; \;,$$北岸的点$${{A}^{′}}$$在$${{A}}$$的正北方向,游船正好到达$${{A}^{′}}$$处时,$$\operatorname{c o s} \theta=$$()
D
A.$$\frac{3 \sqrt{5}} {7}$$
B.$$- \frac{3 \sqrt{5}} {7}$$
C.$$\begin{array} {l l} {\frac{2} {7}} \\ \end{array}$$
D.$$- \frac{2} {7}$$
6、['向量加法的定义及运算法则', '平面向量的概念', '向量在物理中的应用举例']正确率60.0%一只鹰正沿与水平方向成$${{3}{0}^{∘}}$$角的方向向下飞行,直扑猎物,太阳光从头上直照下来,若鹰在地面上的影子的速度大小是$$4 0 ~ \mathrm{m / s},$$则鹰的飞行速度大小为()
C
A.$$\frac{8 0} {3} \ \mathrm{m / s}$$
B.$$\frac{4 0 \sqrt3} {3} \mathrm{{\ m / s}}$$
C.$$\frac{8 0 \sqrt3} {3} \mathrm{{\ m / s}}$$
D.$$\frac{4 0} {3} \ \mathrm{m / s}$$
7、['向量坐标与向量的数量积', '向量在物理中的应用举例']正确率60.0%若两个力$$\overrightarrow{F_{1}}, \ \overrightarrow{F_{2}}$$共同作用于同一物体,$$\overrightarrow{F_{1}}=\overrightarrow{i}+3 \overrightarrow{j}, \ \overrightarrow{F_{2}}=3 \overrightarrow{i}-4 \overrightarrow{j}$$,其中$${{i}^{→}{,}{{j}^{→}}}$$分别是$${{x}{,}{y}}$$轴正方向上的单位向量,当物体从点$$M ( 3, 2 )$$移到点$$M^{\prime} ( 5, 6 )$$时,$$\overrightarrow{F_{1}}, \ \overrightarrow{F_{2}}$$的合力所做的功是()
A
A.$${{4}}$$焦耳
B.$${{5}}$$焦耳
C.$${{6}}$$焦耳
D.$${{8}}$$焦耳
8、['向量在物理中的应用举例']正确率60.0%已知三个力$$\overrightarrow{f_{1}}=(-2$$,$${{−}{1}{)}}$$,$$\vec{f}_{2}^{\rightarrow}=(-3, 2 )$$,$$\overrightarrow{f_{3}}=( 4$$,$${{−}{3}{)}}$$同时作用于某物体上一点,为使物体保持平衡,现在该点处加上一个力$${{{f}_{4}}^{→}}$$,则$${{{f}_{4}}^{→}{=}}$$()
D
A.$${{(}{−}{1}}$$,$${{−}{2}{)}}$$
B.$${{(}{1}}$$,$${{−}{2}{)}}$$
C.$$(-1, 2 )$$
D.$$( 1, 2 )$$
9、['向量在物理中的应用举例']正确率80.0%甲、乙两人提起重量为$${{8}{N}}$$的物体,两人用力方向的夹角为$${{θ}}$$,用力大小分别为$${{6}{N}}$$、$${{7}{N}}$$,则$${{c}{o}{s}{θ}}$$的值为$${{(}{)}}$$
A
A.$$- \frac{1} {4}$$
B.$$\frac{1} {4}$$
C.$$\frac{1} {2}$$
D.$$- \frac{1} {2}$$
10、['向量在物理中的应用举例']正确率80.0%河水的流速为$${{2}{m}{/}{s}}$$,一艘小船想沿垂直于河岸方向以$$1 0 m / s$$的速度驶向对岸,则小船的静水速度大小为$${{(}{)}}$$
B
A.$$1 0 m / s$$
B.$$2 \sqrt{2 6} m / s$$
C.$$4 \sqrt{6} m / s$$
D.$$1 2 m / s$$
1. 首先计算合力 $$\boldsymbol{F} = \boldsymbol{F}_1 + \boldsymbol{F}_2 = (2 + (-5), 4 + 3) = (-3, 7)$$。位移向量 $$\boldsymbol{S} = \overrightarrow{AB} = (2 - 1, 4 - 0) = (1, 4)$$。功的计算公式为 $$W = \boldsymbol{F} \cdot \boldsymbol{S} = (-3) \times 1 + 7 \times 4 = -3 + 28 = 25$$。答案为
A.$${{2}{5}}$$
。2. 力 $$\overrightarrow{F} = (5, 2)$$,位移向量 $$\overrightarrow{AB} = (2 - (-1), 6 - 3) = (3, 3)$$。功的计算公式为 $$W = \overrightarrow{F} \cdot \overrightarrow{AB} = 5 \times 3 + 2 \times 3 = 15 + 6 = 21$$。但选项中没有21,检查计算是否有误。重新计算 $$W = 5 \times 3 + 2 \times 3 = 15 + 6 = 21$$,选项C为21。答案为
C.$${{2}{1}}$$
。3. 三个力平衡,故 $$\overrightarrow{F}_2 = -(\overrightarrow{F}_1 + \overrightarrow{F}_3)$$。先计算 $$\overrightarrow{F}_1 + \overrightarrow{F}_3$$ 的大小,利用余弦定理:$$|\overrightarrow{F}_1 + \overrightarrow{F}_3|^2 = |\overrightarrow{F}_1|^2 + |\overrightarrow{F}_3|^2 + 2|\overrightarrow{F}_1||\overrightarrow{F}_3|\cos 60^\circ = 1 + 4 + 2 \times 1 \times 2 \times 0.5 = 7$$,故 $$|\overrightarrow{F}_2| = \sqrt{7}$$。答案为
C.$${\sqrt {7}{N}}$$
。4. 降落伞匀速下落,合力为零。设每根绳子的拉力为 $$T$$,竖直方向的分力为 $$T \cos 60^\circ = \frac{T}{2}$$。8根绳子的总竖直分力为 $$8 \times \frac{T}{2} = 4T$$,与重力平衡:$$4T = mg = 1 \times 9.8 = 9.8$$,解得 $$T = \frac{9.8}{4} = 2.45 \mathrm{N}$$。答案为
B.$$2. 4 5 ~ \mathrm{N}$$
。5. 游船要正北到达 $$A'$$,则其合速度方向必须正北。设合速度为 $$\overrightarrow{v}$$,则 $$\overrightarrow{v} = \overrightarrow{v}_1 + \overrightarrow{v}_2$$。竖直方向分量为 $$|\overrightarrow{v}_1| \cos \theta + |\overrightarrow{v}_2| \cos 180^\circ = 14 \cos \theta - 4 = 0$$,解得 $$\cos \theta = \frac{4}{14} = \frac{2}{7}$$。但题目选项中有负号,检查水流方向是否相反。若 $$\theta$$ 为钝角,则 $$\cos \theta = -\frac{2}{7}$$。答案为
D.$$- \frac{2} {7}$$
。6. 鹰的飞行速度 $$\overrightarrow{v}$$ 与水平方向成30°,其水平分量为 $$v \cos 30^\circ$$。影子速度为水平分量,故 $$v \cos 30^\circ = 40$$,解得 $$v = \frac{40}{\cos 30^\circ} = \frac{40}{\sqrt{3}/2} = \frac{80}{\sqrt{3}} = \frac{80 \sqrt{3}}{3} \mathrm{m/s}$$。答案为
C.$$\frac{8 0 \sqrt3} {3} \mathrm{{\ m / s}}$$
。7. 合力 $$\overrightarrow{F} = \overrightarrow{F}_1 + \overrightarrow{F}_2 = (1 + 3, 3 + (-4)) = (4, -1)$$。位移向量 $$\overrightarrow{MM'} = (5 - 3, 6 - 2) = (2, 4)$$。功的计算公式为 $$W = \overrightarrow{F} \cdot \overrightarrow{MM'} = 4 \times 2 + (-1) \times 4 = 8 - 4 = 4$$ 焦耳。答案为
A.$${{4}}$$焦耳
。8. 物体平衡时,四个力的合力为零,故 $$\overrightarrow{f}_4 = -(\overrightarrow{f}_1 + \overrightarrow{f}_2 + \overrightarrow{f}_3) = -((-2 -3 + 4), (-1 + 2 -3)) = -(-1, -2) = (1, 2)$$。答案为
D.$$( 1, 2 )$$
。9. 设甲、乙的力为 $$\overrightarrow{F}_1$$ 和 $$\overrightarrow{F}_2$$,合力为 $$\overrightarrow{F}_1 + \overrightarrow{F}_2$$ 与重力平衡。$$|\overrightarrow{F}_1 + \overrightarrow{F}_2| = 8$$。利用余弦定理:$$|\overrightarrow{F}_1 + \overrightarrow{F}_2|^2 = |\overrightarrow{F}_1|^2 + |\overrightarrow{F}_2|^2 + 2|\overrightarrow{F}_1||\overrightarrow{F}_2|\cos \theta$$,即 $$64 = 36 + 49 + 2 \times 6 \times 7 \cos \theta$$,解得 $$\cos \theta = \frac{64 - 85}{84} = \frac{-21}{84} = -\frac{1}{4}$$。答案为
A.$$- \frac{1} {4}$$
。10. 设静水速度为 $$\overrightarrow{v}$$,水流速度为 $$\overrightarrow{u} = (2, 0)$$,合速度垂直于河岸为 $$\overrightarrow{v} + \overrightarrow{u} = (0, 10)$$。故 $$\overrightarrow{v} = (0, 10) - (2, 0) = (-2, 10)$$,其大小为 $$|\overrightarrow{v}| = \sqrt{(-2)^2 + 10^2} = \sqrt{4 + 100} = \sqrt{104} = 2 \sqrt{26} \mathrm{m/s}$$。答案为
B.$$2 \sqrt{2 6} m / s$$
。 题目来源于各渠道收集,若侵权请联系下方邮箱.jpg)