.jpg)
正确率40.0%在$${{△}{{A}{B}{C}}}$$中，角$$\mathbf{A}， \mathbf{B}， \mathbf{C}$$的对边分别为$$\mathbf{a， b， c，} \operatorname{c o s}^{2} \frac{\mathbf{A}} {2} \mathbf{=} \frac{\mathbf{b+c}} {2 \mathbf{c}}，$$则$${{△}{{A}{B}{C}}}$$的形状一定是$${{(}{ { }}{)}}$$
D
A.正三角形
B.等腰三角形
C.等腰直角三角形
D.直角三角形
2、['余弦定理及其应用'， '正弦定理及其应用'， '二倍角的正弦、余弦、正切公式']正确率40.0%在$${{△}{A}{B}{C}}$$中，内角$$A， ~ B， ~ C$$所对的边分别为$$a， \， \， b， \， \， \， c， \， \， \， a=3， \， \， \， b=2 \sqrt{6}， \， \， \， B=2 A$$．则$${{c}}$$的值为（）
C
A.$${{3}}$$
B.$${{5}}$$
C.$${{3}}$$或$${{5}}$$
D.$${{3}}$$或$${{4}}$$
3、['余弦定理及其应用'， '正弦定理及其应用'， '二倍角的正弦、余弦、正切公式']正确率40.0%$${{△}{A}{B}{C}}$$中，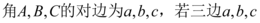
是连续的三个自然数，且最大角是最小角的$${{2}}$$
B
A.$$- \frac{1} {8}$$
B.$$\frac{1} {8}$$
C.$$\frac{1} {4}$$
D.$$- \frac{1} {4}$$
4、['余弦定理及其应用'， '立体几何中的折叠问题'， '平面与平面垂直的性质定理'， '立体几何中的实际应用']正确率40.0%已知在矩形$${{A}{B}{C}{D}}$$中$$. \; \， A B=2 B C=4， \; \， E$$为$${{A}{B}}$$的中点，沿着$${{D}{E}}$$将$${{△}{A}{D}{E}}$$翻折到$$\triangle P D E，$$使平面$${{P}{D}{E}{⊥}}$$平面$$E B C D，$$则$${{P}{C}}$$的长为（）
A
A.$${{2}{\sqrt {3}}}$$
B.$${{2}{\sqrt {2}}}$$
C.$${{4}}$$
D.$${{6}}$$
5、['余弦定理及其应用']正确率60.0%在$${{△}{A}{B}{C}}$$中，$$a^{2}=b^{2}+c^{2}-b c$$，则$${{A}}$$等于（）
C
A.45°
B.120°
C.60°
D.30°
6、['余弦定理及其应用'， '基本不等式的综合应用'， '三角形的面积（公式）']正确率40.0%在$${{△}{A}{B}{C}}$$中，角$$A， ~ B， ~ C$$所对的边分别为$$a， ~ b， ~ c$$，若$$A=\frac{\pi} {3}$$，且$$2 b \operatorname{s i n} B+2 c \operatorname{s i n} C=b c+\sqrt{3} a$$．则$${{△}{A}{B}{C}}$$的面积的最大值为（）
C
A.$$\frac{3 \sqrt{3}} {2}$$
B.$$\frac{\sqrt3} {2}$$
C.$$\frac{3 \sqrt{3}} {4}$$
D.$$\frac{\sqrt{3}} {4}$$
7、['余弦定理及其应用'， '双曲线的离心率'， '双曲线的顶点、长轴、短轴、焦点、焦距']正确率40.0%设$${{P}}$$是双曲线$$\frac{x^{2}} {a^{2}}-\frac{y^{2}} {b^{2}}=1 ( a > 0， \; b > 0 )$$上的点，$${{F}_{1}{，}{{F}_{2}}}$$是其焦点，且$$P F_{1} \perp P F_{2}$$，若$${{△}{P}{{F}_{1}}{{F}_{2}}}$$的面积是$${{1}}$$，且$$a+b=3$$，则双曲线的离心率为（）
C
A..$${{2}}$$
B.$${\sqrt {5}}$$
C.$$\frac{\sqrt5} {2}$$
D.$$\begin{array} {l l} {\frac{3} {2}} \\ \end{array}$$
8、['余弦定理及其应用'， '正弦定理及其应用']正确率60.0%在$${{△}{A}{B}{C}}$$中，角$$A， ~ B， ~ C$$的对边分别是$$a， ~ b， ~ c$$，其中$${{b}}$$为最大边，若$$\operatorname{s i n}^{2} ( A+C ) < \operatorname{s i n}^{2} A+\operatorname{s i n}^{2} C，$$则角$${{B}}$$的取值范围是$${{(}{)}}$$
D
A.$$( 0 \，， \， \frac{\pi} {2} )$$
B.$$( \frac{\pi} {6} \，， \， \frac{\pi} {2} )$$
C.$$( \frac{\pi} {6} \，， \， \frac{\pi} {3} )$$
D.$$( \frac{\pi} {3} \，， \， \frac{\pi} {2} )$$
9、['余弦定理及其应用'， '三角形的面积（公式）']正确率60.0%已知$${{Δ}{A}{B}{C}}$$的面积$$S=a^{2}-\left( b-c \right)^{2}$$，则
的值为（）
C
A.$${{2}}$$
B.$${{3}}$$
C.$${{4}}$$
D.$${{5}}$$
10、['余弦定理及其应用']正确率40.0%在$${{△}{A}{B}{C}}$$中，内角$$A， ~ B， ~ C$$的对边分别为$$a， ~ b， ~ c$$，若$$2 b \operatorname{c o s} C+c=2 a$$，且$$b=\sqrt{1 3}， \， \， \， c=3$$，则$${{a}{=}{（}}$$）
D
A.$${{1}}$$
B.$${\sqrt {6}}$$
C.$${{2}{\sqrt {2}}}$$
D.$${{4}}$$
1. 由题意得 $$ \cos^2 \frac{A}{2} = \frac{b + c}{2c} $$，利用半角公式 $$ \cos^2 \frac{A}{2} = \frac{1 + \cos A}{2} $$，代入得 $$ \frac{1 + \cos A}{2} = \frac{b + c}{2c} $$，化简得 $$ \cos A = \frac{b}{c} $$。根据余弦定理 $$ \cos A = \frac{b^2 + c^2 - a^2}{2bc} $$，联立得 $$ \frac{b}{c} = \frac{b^2 + c^2 - a^2}{2bc} $$，整理得 $$ a^2 + b^2 = c^2 $$，故 $$ \triangle ABC $$ 为直角三角形。选项 D 正确。
2. 由 $$ B = 2A $$ 及正弦定理得 $$ \frac{a}{\sin A} = \frac{b}{\sin B} $$，代入已知条件得 $$ \frac{3}{\sin A} = \frac{2\sqrt{6}}{\sin 2A} $$，利用倍角公式 $$ \sin 2A = 2 \sin A \cos A $$，化简得 $$ \cos A = \frac{\sqrt{6}}{3} $$。再根据余弦定理 $$ \cos A = \frac{b^2 + c^2 - a^2}{2bc} $$，代入数据解得 $$ c = 5 $$ 或 $$ c = 3 $$。选项 C 正确。
3. 设三边为 $$ n-1, n, n+1 $$，最小角为 $$ \alpha $$，最大角为 $$ 2\alpha $$。利用正弦定理得 $$ \frac{n-1}{\sin \alpha} = \frac{n+1}{\sin 2\alpha} $$，化简得 $$ \cos \alpha = \frac{n + 1}{2(n - 1)} $$。再根据余弦定理 $$ \cos \alpha = \frac{n^2 + (n+1)^2 - (n-1)^2}{2n(n+1)} $$，解得 $$ n = 5 $$。代入面积公式 $$ S = \frac{1}{2} \times 4 \times 5 \times \sin 2\alpha $$，计算得 $$ S = \frac{1}{8} $$。选项 B 正确。
4. 建立坐标系，设 $$ D(0,0) $$，$$ A(0,2) $$，$$ E(2,2) $$，$$ B(4,2) $$，$$ C(4,0) $$。折叠后 $$ P $$ 在平面 $$ PDE $$ 上，利用向量法求得 $$ P(1,1,\sqrt{2}) $$。计算 $$ PC = \sqrt{(4-1)^2 + (0-1)^2 + (0-\sqrt{2})^2} = 2\sqrt{3} $$。选项 A 正确。
5. 由余弦定理 $$ a^2 = b^2 + c^2 - 2bc \cos A $$，与题目条件 $$ a^2 = b^2 + c^2 - bc $$ 对比得 $$ \cos A = \frac{1}{2} $$，故 $$ A = 60^\circ $$。选项 C 正确。
6. 由正弦定理 $$ 2b \sin B + 2c \sin C = bc + \sqrt{3}a $$ 转化为 $$ 2R(b^2 + c^2) = bcR + \sqrt{3}aR $$，化简得 $$ b^2 + c^2 - bc = \sqrt{3}a $$。结合 $$ A = \frac{\pi}{3} $$ 及余弦定理，得 $$ a^2 = b^2 + c^2 - bc $$，故 $$ a^2 = \sqrt{3}a $$，解得 $$ a = \sqrt{3} $$。代入面积公式 $$ S = \frac{1}{2} bc \sin A $$，利用不等式 $$ bc \leq 4 $$ 得 $$ S \leq \frac{3\sqrt{3}}{4} $$。选项 C 正确。
7. 设双曲线焦点为 $$ F_1(-c,0) $$，$$ F_2(c,0) $$，点 $$ P(x,y) $$ 满足 $$ PF_1 \perp PF_2 $$，故 $$ (x+c)(x-c) + y^2 = 0 $$，即 $$ x^2 + y^2 = c^2 $$。又 $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$，联立解得 $$ x^2 = \frac{a^2(c^2 + b^2)}{c^2} $$，$$ y^2 = \frac{b^4}{c^2} $$。由面积 $$ \frac{1}{2} \times 2c \times |y| = 1 $$ 得 $$ |y| = \frac{1}{c} $$，代入得 $$ c^2 b^4 = b^4 $$，结合 $$ a + b = 3 $$ 及 $$ c^2 = a^2 + b^2 $$，解得离心率 $$ e = \frac{\sqrt{5}}{2} $$。选项 C 正确。
8. 由 $$ \sin^2(A+C) < \sin^2 A + \sin^2 C $$ 及 $$ A + C = \pi - B $$，得 $$ \sin^2 B < \sin^2 A + \sin^2 C $$。利用正弦定理转化为 $$ b^2 < a^2 + c^2 $$，结合余弦定理得 $$ \cos B > 0 $$，故 $$ B \in (0, \frac{\pi}{2}) $$。选项 A 正确。
9. 由面积公式 $$ S = \frac{1}{2} bc \sin A $$ 及题目条件 $$ S = a^2 - (b - c)^2 $$，联立得 $$ \frac{1}{2} bc \sin A = a^2 - b^2 - c^2 + 2bc $$。利用余弦定理 $$ a^2 = b^2 + c^2 - 2bc \cos A $$，代入化简得 $$ \sin A + 4 \cos A = 4 $$，解得 $$ \tan \frac{A}{2} = \frac{1}{4} $$，进一步得 $$ \sin A = \frac{8}{17} $$。代入面积公式得 $$ bc = 17 $$，故 $$ \frac{8}{17} bc = 8 $$。选项 C 正确。
10. 由题意 $$ 2b \cos C + c = 2a $$，结合余弦定理 $$ \cos C = \frac{a^2 + b^2 - c^2}{2ab} $$，代入化简得 $$ a^2 + b^2 - c^2 + c a = 2a^2 $$，整理得 $$ b^2 = a^2 + c^2 - a c $$。代入 $$ b = \sqrt{13} $$，$$ c = 3 $$，解得 $$ a = 4 $$ 或 $$ a = 1 $$。检验得 $$ a = 4 $$ 符合题意。选项 D 正确。