.jpg)
正确率60.0%以观测者的位置作为原点，东、南、西、北四个方向把平面分成四部分，以正北方向为始边，按顺时针方向旋转$${{2}{8}{0}^{∘}}$$到目标方向线，则目标方向线的位置在观测者（）
C
A.北偏东$${{8}{0}^{∘}}$$的方向
B.南偏东$${{8}{0}^{∘}}$$的方向
C.北偏西$${{8}{0}^{∘}}$$的方向
D.南偏西$${{8}{0}^{∘}}$$的方向
2、['余弦定理及其应用'， '余弦定理、正弦定理应用举例']正确率60.0%已知$${{A}}$$船在灯塔$${{C}}$$的北偏东$${{8}{5}^{∘}}$$方向且$${{A}}$$到$${{C}}$$的距离为$${{2}{k}{m}}$$$${，{B}}$$船在灯塔$${{C}}$$的北偏西$${{6}{5}^{∘}}$$方向且$${{B}}$$到$${{C}}$$的距离为$$\sqrt{3} ~ \mathrm{k m}$$，则$${{A}{，}{B}}$$两船间的距离为（）
A
A.$$\sqrt{1 3} ~ \mathrm{k m}$$
B.$$\sqrt{1 5} ~ \mathrm{k m}$$
C.$${{2}{\sqrt {3}}{k}{m}}$$
D.$${{3}{\sqrt {2}}{k}{m}}$$
3、['余弦定理、正弦定理应用举例']正确率60.0%如图，一艘船自西向东匀速航行，上午$${{1}{0}}$$时到一座灯塔$${{P}}$$的南偏西$${{7}{5}^{∘}}$$距塔$${{6}{8}}$$海里的$${{M}}$$处，下午$${{2}}$$时达这座灯塔的东南方向的$${{N}}$$处，且$$\angle M N P=4 5^{\circ}$$，则这艘船航行的速度为（）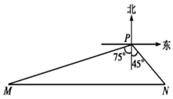
A
A.$$\frac{1 7 \sqrt6} {2}$$海里$${{/}}$$时
B.$${{3}{4}{\sqrt {6}}}$$海里$${{/}}$$时
C.$$\frac{1 7 \sqrt2} {2}$$海里$${{/}}$$时
D.$${{3}{4}{\sqrt {2}}}$$海里$${{/}}$$时
4、['余弦定理、正弦定理应用举例']正确率40.0%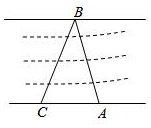
如图，设$${{A}{、}{B}}$$
A
A.$${{5}{0}{\sqrt {6}}{m}}$$
B.$${{5}{0}{\sqrt {3}}}$$$${{m}}$$
C.$$\frac{5 0} {3} \， ( 3 \sqrt{2}+\sqrt{6} ) \， \， \， m$$
D.$$5 0 ~ ( \sqrt{3}+1 ) ~ m$$
5、['余弦定理、正弦定理应用举例']正确率60.0%一海轮从$${{A}}$$处出发，以每小时$${{4}{0}}$$海里的速度沿南偏东$${{4}{0}^{∘}}$$的方向直线航行$${，{{3}{0}}}$$分钟后到达$${{B}}$$处.在$${{C}}$$处有一座灯塔，海轮在$${{A}}$$处观察灯塔，其方向是南偏东$${{7}{0}^{∘}{，}}$$在$${{B}}$$处观察灯塔，其方向是北偏东$${{6}{5}^{∘}{，}}$$那么$${{B}{，}{C}}$$两点间的距离是（）
B
A.$${{1}{0}{\sqrt {3}}}$$海里
B.$${{1}{0}{\sqrt {2}}}$$海里
C.$${{2}{0}{\sqrt {3}}}$$海里
D.$${{2}{0}{\sqrt {2}}}$$海里
6、['余弦定理、正弦定理应用举例']正确率60.0%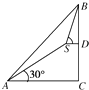
如图，在山根$${{A}}$$
B
A.$${{5}{0}{0}}$$米
B.$${{1}{0}{0}{0}}$$米
C.$${{1}{2}{0}{0}}$$米
D.$${{1}{5}{0}{0}}$$米
7、['余弦定理、正弦定理应用举例']正确率60.0%已知两灯塔$${{A}}$$和$${{B}}$$与海洋观测站$${{C}}$$的距离都等于$${{2}{0}{k}{m}}$$，灯塔$${{A}}$$在观测站$${{C}}$$的北偏东$${{3}{0}^{o}}$$，灯塔$${{B}}$$在观测站$${{C}}$$的南偏东$${{6}{0}^{o}}$$，则灯塔$${{A}}$$与灯塔$${{B}}$$的距离为$${{(}{)}}$$
D
A.$${{2}{0}{k}{m}}$$
B.$${{4}{0}{k}{m}}$$
C.$$2 0 \sqrt{3} k m$$
D.$$2 0 \sqrt{2} k m$$
正确率60.0%如图，位于$${{A}}$$处的海面观测站获悉，在其正东方向相距$${{4}{0}}$$海里的$${{B}}$$处有一艘渔船遇险，并在原地等待营救．在$${{A}}$$处南偏西$${{3}{0}^{∘}}$$且相距$${{2}{0}}$$海里的$${{C}}$$处有一艘救援船，则该船到求助处$${{B}}$$的距离为（）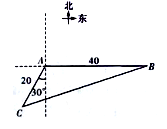
D
A.$${{2}{8}{0}{0}}$$海里
B.$${{1}{2}{0}{0}}$$海里
C.$${{2}{0}{\sqrt {3}}}$$海里
D.$${{2}{0}{\sqrt {7}}}$$海里
9、['余弦定理、正弦定理应用举例']正确率40.0%在$${{2}{0}{0}{m}}$$高的山顶上，测得山下一塔的塔顶与塔底的俯角分别是$$3 0^{\circ} \，， \， \， 6 0^{\circ} \，，$$则塔高为（）
C
A.$$\frac{2 0 0} {3} \textrm{m}$$
B.$${{1}{0}{0}{m}}$$
C.$$\frac{4 0 0} {3} \textrm{m}$$
D.$${{9}{0}{m}}$$
10、['余弦定理、正弦定理应用举例']正确率40.0%如图，为了测量河对岸$${{A}{，}{B}}$$两点间的距离，沿河岸选取相距$${{4}{0}}$$米的$${{C}{，}{D}}$$两点，测得$$\angle A C B=6 0^{\circ} \，， \， \， \， \angle B C D=4 5^{\circ} \，，$$$$\angle A D B=6 0^{\circ} \，， \， \， \angle A D C=3 0^{\circ} \，，$$则$${{A}{，}{B}}$$两点间的距离是（）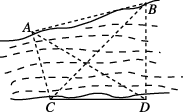
D
A.$${{2}{0}{\sqrt {2}}}$$米
B.$${{2}{0}{\sqrt {3}}}$$米
C.$${{4}{0}{\sqrt {2}}}$$米
D.$${{2}{0}{\sqrt {6}}}$$米
1. 解析：
正北方向为始边，顺时针旋转$$280^\circ$$，相当于从正北方向向东旋转$$280^\circ - 270^\circ = 10^\circ$$，即南偏西$$80^\circ$$（因为$$270^\circ$$是正西方向，再转$$10^\circ$$靠近南方）。因此答案为D。
2. 解析：
根据题意，$$A$$船在灯塔$$C$$的北偏东$$85^\circ$$方向，$$B$$船在灯塔$$C$$的北偏西$$65^\circ$$方向，两方向的夹角为$$85^\circ + 65^\circ = 150^\circ$$。利用余弦定理计算$$AB$$的距离：
$$AB = \sqrt{AC^2 + BC^2 - 2 \cdot AC \cdot BC \cdot \cos(150^\circ)}$$
代入$$AC = 2\,\text{km}$$，$$BC = \sqrt{3}\,\text{km}$$，$$\cos(150^\circ) = -\frac{\sqrt{3}}{2}$$，得：
$$AB = \sqrt{4 + 3 + 2 \cdot 2 \cdot \sqrt{3} \cdot \frac{\sqrt{3}}{2}} = \sqrt{13}\,\text{km}$$。因此答案为A。
3. 解析：
从上午10时到下午2时共4小时。在$$\triangle MNP$$中，$$\angle MNP = 45^\circ$$，$$\angle MPN = 75^\circ + 45^\circ = 120^\circ$$，利用正弦定理：
$$\frac{MN}{\sin(120^\circ)} = \frac{MP}{\sin(45^\circ)}$$
代入$$MP = 68$$海里，得：
$$MN = \frac{68 \cdot \sin(120^\circ)}{\sin(45^\circ)} = \frac{68 \cdot \frac{\sqrt{3}}{2}}{\frac{\sqrt{2}}{2}} = 34\sqrt{6}$$海里。
速度为$$\frac{34\sqrt{6}}{4} = \frac{17\sqrt{6}}{2}$$海里/时。因此答案为A。
5. 解析：
海轮从$$A$$到$$B$$的航行距离为$$40 \times 0.5 = 20$$海里。在$$\triangle ABC$$中，$$\angle BAC = 70^\circ - 40^\circ = 30^\circ$$，$$\angle ABC = 180^\circ - 65^\circ - 40^\circ = 75^\circ$$，$$\angle ACB = 180^\circ - 30^\circ - 75^\circ = 75^\circ$$。利用正弦定理：
$$\frac{BC}{\sin(30^\circ)} = \frac{AB}{\sin(75^\circ)}$$
代入$$AB = 20$$海里，得：
$$BC = \frac{20 \cdot \sin(30^\circ)}{\sin(75^\circ)} = \frac{20 \cdot 0.5}{\frac{\sqrt{6} + \sqrt{2}}{4}} = 10\sqrt{2}$$海里。因此答案为B。
7. 解析：
灯塔$$A$$在观测站$$C$$的北偏东$$30^\circ$$，灯塔$$B$$在观测站$$C$$的南偏东$$60^\circ$$，两方向的夹角为$$180^\circ - 30^\circ - 60^\circ = 90^\circ$$。利用勾股定理计算$$AB$$的距离：
$$AB = \sqrt{AC^2 + BC^2} = \sqrt{20^2 + 20^2} = 20\sqrt{2}\,\text{km}$$。因此答案为D。
8. 解析：
在$$\triangle ABC$$中，$$AC = 20$$海里，$$AB = 40$$海里，$$\angle CAB = 30^\circ$$。利用余弦定理计算$$BC$$的距离：
$$BC = \sqrt{AC^2 + AB^2 - 2 \cdot AC \cdot AB \cdot \cos(30^\circ)}$$
代入数据，得：
$$BC = \sqrt{400 + 1600 - 800\sqrt{3}} = \sqrt{2000 - 800\sqrt{3}} \approx 20\sqrt{7}$$海里。因此答案为D。
9. 解析：
设塔高为$$h$$，山顶到塔底的距离为$$x$$。根据俯角关系：
$$\tan(60^\circ) = \frac{200}{x} \Rightarrow x = \frac{200}{\sqrt{3}}$$
$$\tan(30^\circ) = \frac{200 - h}{x} \Rightarrow 200 - h = \frac{200}{\sqrt{3}} \cdot \frac{1}{\sqrt{3}} = \frac{200}{3}$$
解得$$h = 200 - \frac{200}{3} = \frac{400}{3}\,\text{m}$$。因此答案为C。
10. 解析：
在$$\triangle ACD$$中，$$\angle ACD = 60^\circ + 45^\circ = 105^\circ$$，$$\angle ADC = 30^\circ$$，$$\angle CAD = 45^\circ$$。利用正弦定理：
$$\frac{AC}{\sin(30^\circ)} = \frac{CD}{\sin(45^\circ)}$$
代入$$CD = 40$$米，得：
$$AC = \frac{40 \cdot 0.5}{\frac{\sqrt{2}}{2}} = 20\sqrt{2}$$米。
在$$\triangle BCD$$中，$$\angle BCD = 45^\circ$$，$$\angle BDC = 60^\circ$$，$$\angle CBD = 75^\circ$$。利用正弦定理：
$$\frac{BC}{\sin(60^\circ)} = \frac{CD}{\sin(75^\circ)}$$
解得$$BC = \frac{40 \cdot \frac{\sqrt{3}}{2}}{\frac{\sqrt{6} + \sqrt{2}}{4}} = 20\sqrt{6} - 20\sqrt{2}$$米。
在$$\triangle ABC$$中，利用余弦定理：
$$AB = \sqrt{AC^2 + BC^2 - 2 \cdot AC \cdot BC \cdot \cos(105^\circ)}$$
化简后得$$AB = 20\sqrt{6}$$米。因此答案为D。