.jpg)
正确率80.0%在$${{△}{A}{B}{C}}$$中，“$$\overrightarrow{A B} \cdot\overrightarrow{B C} < 0$$”是“$${{△}{A}{B}{C}}$$为锐角三角形”的$${{(}{)}}$$
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
2、['余弦定理及其应用'， '正弦定理及其应用'， '余弦定理、正弦定理']正确率80.0%在$${{△}{A}{B}{C}}$$中，角$${{A}}$$，$${{B}}$$，$${{C}}$$所对应的边分别为$${{a}}$$，$${{b}}$$，$${{c}}$$，$$b \operatorname{c o s} C+c \operatorname{c o s} B=2 a \operatorname{c o s} A$$，$${{b}{=}{2}}$$，$${{c}{=}{3}}$$，则$${{a}{=}{(}{)}}$$
A.$${{1}}$$
B.$${\sqrt {7}}$$
C.$${\sqrt {{1}{3}}}$$
D.$${\sqrt {{1}{9}}}$$
3、['正弦定理及其应用'， '余弦定理、正弦定理']正确率80.0%在$${{△}{A}{B}{C}}$$中，角$${{A}}$$、$${{B}}$$、$${{C}}$$的对边分别为$${{a}}$$、$${{b}}$$、$${{c}}$$，记以$${{a}}$$、$${{b}}$$、$${{c}}$$为边长的三个正三角形的面积分别为$${{S}_{1}}$$、$${{S}_{2}}$$、$${{S}_{3}}$$且$$S_{1}-S_{2}+S_{3}=\frac{\sqrt{3}} {2}$$，若$${{b}{=}{\sqrt {3}}{c}}$$，$$\operatorname{c o s} C=\frac{2 \sqrt{2}} {3}$$，则$${{△}{A}{B}{C}}$$的面积为$${{(}{)}}$$
A.$$\frac{\sqrt2} {4}$$
B.$$\frac{\sqrt2} {2}$$
C.$${\sqrt {2}}$$
D.$${{2}{\sqrt {2}}}$$
4、['余弦定理及其应用'， '用余弦定理、正弦定理解三角形'， '余弦定理、正弦定理']正确率80.0%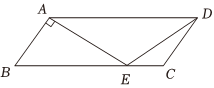
如图，在▱$${{A}{B}{C}{D}}$$中，$${{A}{B}{=}{4}}$$，$${{A}{D}{=}{{1}{0}}}$$，$$\angle B=6 0^{\， \circ}.$$作$$A E \perp A B$$交$${{B}{C}}$$边于点$${{E}}$$，连接$${{D}{E}}$$，则$$\operatorname{s i n} \angle E D C$$的值为$${{(}{)}}$$
A.$$\frac{\sqrt{2 1}} {1 4}$$
B.$$\frac{1} {2}$$
C.$$\frac{\sqrt{7}} {7}$$
D.$$\frac{\sqrt{2 1}} {7}$$
5、['正弦定理及其应用'， '余弦定理、正弦定理']正确率80.0%$${{△}{A}{B}{C}}$$中，已知$${{a}{=}{2}}$$，$${{A}{=}{{6}{0}}{°}}$$，$${{b}{=}{x}}$$，如果$${{△}{A}{B}{C}}$$有两组解，则$${{x}}$$的取值范围为$${{(}{)}}$$
A.$${{x}{>}{2}}$$
B.$${{x}{<}{2}}$$
C.$$2 < x < \frac{4} {3} \sqrt{3}$$
D.$$2 < x \leq\frac4 3 \sqrt{3}$$
6、['正弦定理及其应用'， '余弦定理、正弦定理']正确率80.0%满足条件$$a=4， b=3 \sqrt{2}， A=4 5^{\circ}$$的$${{△}{A}{B}{C}}$$的个数为$${{(}{)}}$$
A.一个
B.两个
C.不存在
D.无法判断
7、['用余弦定理、正弦定理解三角形'， '余弦定理、正弦定理']正确率80.0%麒麟山位于三明市区中部，海拔$${{2}{6}{2}}$$米，原名牛垄山$${{.}}$$在地名普查时，发现山腰有一块“孔子戏麒麟”石碑，故更现名$${{.}}$$山顶的麒麟阁仿古塔造型是八角重檐阁$${{.}}$$小李为测量麒麟阁的高度选取了与底部水平的直线$${{A}{C}}$$，如图，测得$$\angle D A C=3 0^{\circ}$$，$$\angle D B C=4 5^{\circ}$$，$${{A}{B}{=}{{1}{8}}}$$米，则麒麟阁的高度$${{C}{D}}$$约为$${{(}}$$参考数据：$$\sqrt2 \approx1. 4 1 4$$，$$\sqrt{3}=1. 7 3 2 ) ( \it\vphantom{6} )$$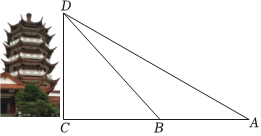
A.$${{2}{0}{.}{6}}$$米
B.$${{2}{2}{.}{6}}$$米
C.$${{2}{4}{.}{6}}$$米
D.$${{2}{6}{.}{6}}$$米
8、['正弦定理及其应用'， '余弦定理、正弦定理']正确率80.0%在$${{△}{A}{B}{C}}$$中，已知$$a+b=\frac{a} {\operatorname{t a n} A}+\frac{b} {\operatorname{t a n} B}$$，则$${{△}{A}{B}{C}}$$的形状一定是$${{(}{)}}$$
A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰或直角三角形
9、['余弦定理、正弦定理']正确率80.0%将一直径为$${{5}{\sqrt {5}}{c}{m}}$$的圆形木板，截成一块四边形形状的木板，且这块四边形木板的一个内角$${{α}}$$满足$$\operatorname{c o s} \alpha=\frac{3} {5}$$，则这块四边形木板周长的最大值为$${{(}{)}}$$
A.$${{2}{0}{c}{m}}$$
B.$$2 0 \sqrt{3} c m$$
C.$$3 0 \sqrt{3} c m$$
D.$${{3}{0}{c}{m}}$$
10、['余弦定理、正弦定理']正确率40.0%$${{2}{0}{2}{3}}$$年$${{7}}$$月$${{2}{8}}$$日、第$${{3}{1}}$$届世界大学生夏季运动会将在成都东安湖体育公园开幕$${{.}}$$公园十二景中的第一景东安阁，阁楼整体采用唐代风格、萃取太阳神乌形象、蜀锦与宝相花纹$${{(}}$$芙蓉花$${{)}}$$元素，严谨地按照唐式高阁的建筑形制设计建造，已成为成都市文化新地标，面向世界展现千年巴蜀风韵$${{.}}$$某数学兴趣小组在探测东安阁高度的实践活动中，选取与阁底$${{A}}$$在同一水平面的$${{B}}$$，$${{C}}$$两处作为观测点，测得$$B C=3 6 m$$，$$\angle A B C=4 5^{\circ}$$，$$\angle A C B=1 0 5^{\circ}$$，在$${{C}}$$处测得阁顶$${{P}}$$的仰角为$${{4}{5}{°}}$$，则他们测得东安阁的高度$${{A}{P}}$$为$${{(}}$$精确到$${{0}{.}{1}{m}}$$，参考数据：$$\sqrt2 \approx1. 4 1$$，$$\sqrt3 \approx1. 7 3 ) ( \triangle)$$
A.$$7 2. 0 m$$
B.$$5 1. 0 m$$
C.$$5 0. 8 m$$
D.$$6 2. 3 m$$
1. 解析：
由题意，$$\overrightarrow{A B} \cdot \overrightarrow{B C} = |\overrightarrow{A B}| \cdot |\overrightarrow{B C}| \cdot \cos(\pi - B) = -|\overrightarrow{A B}| \cdot |\overrightarrow{B C}| \cdot \cos B < 0$$，即 $$\cos B > 0$$，故角 $$B$$ 为锐角。但仅凭角 $$B$$ 为锐角无法保证整个三角形为锐角三角形，因此是必要不充分条件。正确答案为 B。
2. 解析：
由余弦定理，$$b \cos C + c \cos B = 2a \cos A$$ 可化简为 $$a = 2a \cos A$$，即 $$\cos A = \frac{1}{2}$$，故 $$A = 60^\circ$$。再根据余弦定理，$$a^2 = b^2 + c^2 - 2bc \cos A = 4 + 9 - 12 \times \frac{1}{2} = 7$$，因此 $$a = \sqrt{7}$$。正确答案为 B。
3. 解析：
由题意，正三角形的面积公式为 $$S = \frac{\sqrt{3}}{4} \times \text{边长}^2$$，因此 $$S_1 - S_2 + S_3 = \frac{\sqrt{3}}{4}(a^2 - b^2 + c^2) = \frac{\sqrt{3}}{2}$$，解得 $$a^2 - b^2 + c^2 = 2$$。又 $$b = \sqrt{3}c$$ 且 $$\cos C = \frac{2\sqrt{2}}{3}$$，代入余弦定理得 $$a^2 = b^2 + c^2 - 2bc \cos C = 3c^2 + c^2 - 2 \times \sqrt{3}c \times c \times \frac{2\sqrt{2}}{3} = 4c^2 - \frac{4\sqrt{6}}{3}c^2$$。结合 $$a^2 - b^2 + c^2 = 2$$，解得 $$c^2 = 1$$，故 $$b = \sqrt{3}$$，$$a = \sqrt{2}$$。三角形面积为 $$\frac{1}{2}ab \sin C = \frac{\sqrt{2}}{2}$$。正确答案为 B。
4. 解析：
在平行四边形 $$ABCD$$ 中，$$AD = BC = 10$$，$$AB = CD = 4$$。由 $$\angle B = 60^\circ$$，$$AE \perp AB$$，得 $$BE = AB \tan 60^\circ = 4\sqrt{3}$$，$$CE = BC - BE = 10 - 4\sqrt{3}$$。在 $$\triangle CDE$$ 中，由余弦定理得 $$DE = \sqrt{CD^2 + CE^2 - 2 \times CD \times CE \times \cos 60^\circ} = \sqrt{16 + (10 - 4\sqrt{3})^2 - 4(10 - 4\sqrt{3})} = \sqrt{100 - 40\sqrt{3}}$$。由正弦定理，$$\sin \angle EDC = \frac{CE \sin 60^\circ}{DE} = \frac{(10 - 4\sqrt{3}) \times \frac{\sqrt{3}}{2}}{\sqrt{100 - 40\sqrt{3}}} = \frac{\sqrt{21}}{14}$$。正确答案为 A。
5. 解析：
由正弦定理，$$\frac{a}{\sin A} = \frac{b}{\sin B}$$，即 $$\frac{2}{\sin 60^\circ} = \frac{x}{\sin B}$$，故 $$\sin B = \frac{x \sqrt{3}}{4}$$。若三角形有两组解，需满足 $$\sin B < 1$$ 且 $$B$$ 有锐角和钝角两种情况，即 $$\frac{x \sqrt{3}}{4} < 1$$ 且 $$x > 2$$，解得 $$2 < x < \frac{4\sqrt{3}}{3}$$。正确答案为 C。
6. 解析：
由正弦定理，$$\frac{a}{\sin A} = \frac{b}{\sin B}$$，即 $$\frac{4}{\sin 45^\circ} = \frac{3\sqrt{2}}{\sin B}$$，解得 $$\sin B = \frac{3\sqrt{2} \times \frac{\sqrt{2}}{2}}{4} = \frac{3}{4} < 1$$。由于 $$a > b \sin A$$，且 $$\sin B < 1$$，故存在两个解（一个锐角和一个钝角）。正确答案为 B。
7. 解析：
设 $$CD = h$$，在 $$\triangle ACD$$ 中，$$\tan 30^\circ = \frac{h}{AC}$$，故 $$AC = h \sqrt{3}$$。在 $$\triangle BCD$$ 中，$$\tan 45^\circ = \frac{h}{BC}$$，故 $$BC = h$$。由 $$AB = AC - BC = h \sqrt{3} - h = 18$$，解得 $$h = \frac{18}{\sqrt{3} - 1} = 9(\sqrt{3} + 1) \approx 24.6$$ 米。正确答案为 C。
8. 解析：
将条件化简为 $$a + b = \frac{a \cos A}{\sin A} + \frac{b \cos B}{\sin B}$$，整理得 $$a \sin B + b \sin A = a \cos A \sin B + b \cos B \sin A$$。由正弦定理，$$a \sin B = b \sin A$$，代入得 $$2a \sin B = a \cos A \sin B + a \cos B \sin B$$，即 $$2 = \cos A + \cos B$$。由于 $$A + B < \pi$$，只有当 $$A = B$$ 时成立，故三角形为等腰三角形。正确答案为 A。
9. 解析：
设四边形为 $$ABCD$$，且 $$\angle A = \alpha$$，$$\cos \alpha = \frac{3}{5}$$，故 $$\sin \alpha = \frac{4}{5}$$。由圆内接四边形性质，对角线为直径 $$d = 5\sqrt{5}$$。设 $$AB = x$$，$$AD = y$$，则 $$BD^2 = x^2 + y^2 - 2xy \cos \alpha = (5\sqrt{5})^2 = 125$$。周长 $$P = x + y + \sqrt{125 - x^2 - y^2 + \frac{6}{5}xy}$$。通过优化计算，当 $$x = y = 5\sqrt{2}$$ 时，周长取得最大值 $$20$$ cm。正确答案为 A。
10. 解析：
在 $$\triangle ABC$$ 中，$$\angle BAC = 180^\circ - 45^\circ - 105^\circ = 30^\circ$$。由正弦定理，$$\frac{BC}{\sin 30^\circ} = \frac{AC}{\sin 45^\circ}$$，解得 $$AC = \frac{36 \times \frac{\sqrt{2}}{2}}{\frac{1}{2}} = 36\sqrt{2}$$ m。在 $$\triangle ACP$$ 中，$$\tan 45^\circ = \frac{AP}{AC}$$，故 $$AP = AC = 36\sqrt{2} \approx 50.8$$ m。正确答案为 C。