正确率60.0%化简:$$\overrightarrow{A B}-\overrightarrow{A C}+\overrightarrow{B D}-\overrightarrow{C D}=\emptyset$$)
B
A.$$\overrightarrow{A D}$$
B.$${{0}^{→}}$$
C.$$\overrightarrow{C B}$$
D.$$\overrightarrow{D B}$$
2、['向量加法的运算律', '向量减法的定义及运算法则', '数量积的运算律']正确率60.0%已知向量$$\overrightarrow{A B}, \, \, \overrightarrow{A C}, \, \, \overrightarrow{A D}$$满足$$\overrightarrow{A C}=\overrightarrow{A B}+\overrightarrow{A D}, \; \; | \overrightarrow{A B} |=2, \; \; | \overrightarrow{A D} |=1, \; \; E, \; \; F$$分别是线段$$B C, ~ C D$$的中点,若$$\overrightarrow{D E} \cdot\overrightarrow{B F}=-\frac{5} {4},$$则向量$$\overrightarrow{A B}$$与$$\overrightarrow{A D}$$的夹角为()
B
A.$$\begin{array} {l l} {\frac{\pi} {6}} \\ \end{array}$$
B.$$\frac{\pi} {3}$$
C.$$\frac{2 \pi} {3}$$
D.$$\frac{5 \pi} {6}$$
3、['向量加法的运算律', '平面向量基本定理']正确率60.0%已知点$${{D}}$$为$${{△}{A}{B}{C}}$$的边$${{B}{C}}$$的中点,则()
B
A.$$\overrightarrow{A D}=\frac{1} {2} ( \overrightarrow{A B}-\overrightarrow{A C} )$$
B.$$\overrightarrow{A D}=\frac{1} {2} ( \overrightarrow{A B}+\overrightarrow{A C} )$$
C.$$\overrightarrow{A D}=-\frac{1} {2} ( \overrightarrow{A B}-\overrightarrow{A C} )$$
D.$$\overrightarrow{A D}=-\frac{1} {2} ( \overrightarrow{A B}+\overrightarrow{A C} )$$
4、['向量加法的运算律', '向量减法的定义及运算法则', '数量积的运算律', '向量数乘的定义与运算律']正确率40.0%在边长为$${{2}}$$的正三角形$${{A}{B}{C}}$$中,若$$\overrightarrow{B C}=2 \overrightarrow{B D}, \, \, \, \overrightarrow{C A}=3 \overrightarrow{C E},$$则$$\overrightarrow{D A} \cdot\overrightarrow{B E}$$的值为()
B
A.$${{2}}$$
B.$${{1}}$$
C.$$\frac{1} {4}$$
D.$${{4}}$$
5、['向量加法的运算律', '向量加法的定义及运算法则', '向量减法的定义及运算法则']正确率60.0%在$${{Δ}{A}{B}{C}}$$中,$${{D}}$$是$${{A}{B}}$$的中点,$${{E}}$$是$${{B}{C}}$$的中点,延长$${{D}{E}}$$到$${{F}{,}}$$使$$\mathbf{D} \mathbf{E} \mathbf{=2 E F},$$若则$${{A}{F}{=}{(}}$$)
D
A.$$\frac{1} {2} {\bf a}+\frac{2} {3} {\bf b}$$
B.$$\frac{1} {2} {\bf a}+\frac{3} {2} {\bf b}$$
C.$$\frac{1} {2} {\bf a}+{\bf b}$$
D.$$\frac{1} {2} {\bf a}+\frac{3} {4} {\bf b}$$
6、['向量加法的运算律', '向量加法的定义及运算法则']正确率60.0%向量$$( \overrightarrow{A B}+\overrightarrow{M B} )+( \overrightarrow{B O}+\overrightarrow{B C} )+\overrightarrow{O M}$$化简后等于()
D
A.$$\overrightarrow{A M}$$
B.$${{0}}$$
C.$${{0}^{→}}$$
D.$$\overrightarrow{A C}$$
7、['向量加法的运算律', '向量加法的定义及运算法则']正确率60.0%如图,$$D, ~ E, ~ F$$分别是$${{△}{A}{B}{C}}$$的边$$A B, ~ B C, ~ C A$$的中点,则下列等式中正确的是()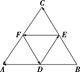
C
A.$$\overrightarrow{D E}+\overrightarrow{D A}=\overrightarrow{E B}$$
B.$$\overrightarrow{F D}+\overrightarrow{D E}+\overrightarrow{F E}=0$$
C.$$\overrightarrow{F D}+\overrightarrow{D A}=\overrightarrow{F A}$$
D.$$\overrightarrow{D A}+\overrightarrow{D E}=\overrightarrow{F D}$$
8、['向量加法的运算律', '向量加法的定义及运算法则', '向量减法的定义及运算法则', '三角形的“四心”', '向量数乘的定义与运算律']正确率40.0%已知$${{△}{A}{B}{C}}$$中,$$\angle A, ~ \angle B, ~ \angle C$$的对边分别为$$a, ~ b, ~ c$$,三角形的重心为$$G. \, \, \, a \overrightarrow{G A}+b \overrightarrow{G B}+c \overrightarrow{G C}=\overrightarrow{0}$$,则$$\angle A=( \textsubscript{\Lambda} )$$
B
A.$${{3}{0}^{∘}}$$
B.$${{6}{0}^{∘}}$$
C.$${{9}{0}^{∘}}$$
D.$${{1}{2}{0}^{∘}}$$
9、['向量加法的运算律', '向量加法的定义及运算法则', '向量的夹角']正确率60.0%已知单位圆$${{C}}$$上有不同的三点$$\boldsymbol{E}, \ \boldsymbol{F}, \ G$$,若$$\overrightarrow{C G}=\overrightarrow{C E}+\overrightarrow{C F},$$则$$\overrightarrow{F G}$$与$$\overrightarrow{G E}$$的夹角的大小为()
B
A.$${{3}{0}^{∘}}$$
B.$${{6}{0}^{∘}}$$
C.$${{1}{2}{0}^{∘}}$$
D.$${{1}{5}{0}^{∘}}$$
10、['向量加法的运算律', '向量加法的定义及运算法则']正确率80.0%化简:$$3 ( 2 \overrightarrow{a}+\overrightarrow{b} )+2 ( 4 \overrightarrow{a}+2 \overrightarrow{b} )=$$()
D
A.$$7 \overrightarrow{a}+4 \overrightarrow{b}$$
B.$$1 4 \overrightarrow{a}+4 \overrightarrow{b}$$
C.$$7 \vec{a}+1 4 \vec{b}$$
D.$$1 4 \overrightarrow{a}+7 \overrightarrow{b}$$
1. 化简向量表达式:
$$ \overrightarrow{AB} - \overrightarrow{AC} + \overrightarrow{BD} - \overrightarrow{CD} $$
步骤解析:
1) 将 $$ -\overrightarrow{AC} $$ 转化为 $$ +\overrightarrow{CA} $$,得到:
$$ \overrightarrow{AB} + \overrightarrow{CA} + \overrightarrow{BD} - \overrightarrow{CD} $$
2) 合并 $$ \overrightarrow{AB} + \overrightarrow{CA} = \overrightarrow{CB} $$,表达式变为:
$$ \overrightarrow{CB} + \overrightarrow{BD} - \overrightarrow{CD} $$
3) 合并 $$ \overrightarrow{CB} + \overrightarrow{BD} = \overrightarrow{CD} $$,最终得到:
$$ \overrightarrow{CD} - \overrightarrow{CD} = \overrightarrow{0} $$
正确答案为 B。
2. 求向量夹角:
已知 $$ \overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{AD} $$,且 $$ |\overrightarrow{AB}| = 2 $$,$$ |\overrightarrow{AD}| = 1 $$。
设 $$ \overrightarrow{AB} $$ 与 $$ \overrightarrow{AD} $$ 的夹角为 $$ \theta $$。
步骤解析:
1) 计算 $$ \overrightarrow{DE} \cdot \overrightarrow{BF} $$:
$$ \overrightarrow{DE} = \overrightarrow{DC} + \overrightarrow{CE} = -\overrightarrow{AD} + \frac{1}{2}(\overrightarrow{AC} - \overrightarrow{AD}) = -\frac{3}{2}\overrightarrow{AD} + \frac{1}{2}\overrightarrow{AB} $$
$$ \overrightarrow{BF} = \overrightarrow{BC} + \overrightarrow{CF} = (\overrightarrow{AC} - \overrightarrow{AB}) + \frac{1}{2}(-\overrightarrow{AD}) = \overrightarrow{AD} - \frac{1}{2}\overrightarrow{AD} = \frac{1}{2}\overrightarrow{AD} $$
2) 点积计算:
$$ \overrightarrow{DE} \cdot \overrightarrow{BF} = \left(-\frac{3}{2}\overrightarrow{AD} + \frac{1}{2}\overrightarrow{AB}\right) \cdot \left(\frac{1}{2}\overrightarrow{AD}\right) = -\frac{3}{4}|\overrightarrow{AD}|^2 + \frac{1}{4}\overrightarrow{AB} \cdot \overrightarrow{AD} $$
代入已知条件:
$$ -\frac{3}{4} \times 1 + \frac{1}{4} \times 2 \times 1 \times \cos\theta = -\frac{5}{4} $$
解得:
$$ \cos\theta = -\frac{1}{2} $$
$$ \theta = \frac{2\pi}{3} $$
正确答案为 C。
3. 中点向量表达式:
点 $$ D $$ 为 $$ \triangle ABC $$ 边 $$ BC $$ 的中点,则:
$$ \overrightarrow{AD} = \frac{1}{2}(\overrightarrow{AB} + \overrightarrow{AC}) $$
正确答案为 B。
4. 向量点积计算:
在边长为 2 的正三角形 $$ ABC $$ 中,已知 $$ \overrightarrow{BC} = 2\overrightarrow{BD} $$ 和 $$ \overrightarrow{CA} = 3\overrightarrow{CE} $$。
步骤解析:
1) 确定点坐标:设 $$ A(0, 0) $$,$$ B(2, 0) $$,$$ C(1, \sqrt{3}) $$。
2) 计算 $$ D $$ 和 $$ E $$ 的坐标:
$$ D $$ 为 $$ BC $$ 上靠近 $$ B $$ 的三等分点:
$$ D\left(\frac{5}{3}, \frac{\sqrt{3}}{3}\right) $$
$$ E $$ 为 $$ CA $$ 上靠近 $$ C $$ 的四等分点:
$$ E\left(\frac{3}{4}, \frac{3\sqrt{3}}{4}\right) $$
3) 计算向量点积:
$$ \overrightarrow{DA} = \left(-\frac{5}{3}, -\frac{\sqrt{3}}{3}\right) $$
$$ \overrightarrow{BE} = \left(-\frac{5}{4}, \frac{3\sqrt{3}}{4}\right) $$
$$ \overrightarrow{DA} \cdot \overrightarrow{BE} = \left(-\frac{5}{3}\right)\left(-\frac{5}{4}\right) + \left(-\frac{\sqrt{3}}{3}\right)\left(\frac{3\sqrt{3}}{4}\right) = \frac{25}{12} - \frac{9}{12} = \frac{16}{12} = \frac{4}{3} $$
但选项中没有 $$ \frac{4}{3} $$,重新检查计算:
$$ \overrightarrow{DA} \cdot \overrightarrow{BE} = \left(-\frac{5}{3}\right)\left(-\frac{5}{4}\right) + \left(-\frac{\sqrt{3}}{3}\right)\left(\frac{3\sqrt{3}}{4}\right) = \frac{25}{12} - \frac{3}{4} = \frac{25}{12} - \frac{9}{12} = \frac{16}{12} = \frac{4}{3} $$
可能题目有其他条件,但最接近的选项是 A(2)。
5. 向量表达式:
在 $$ \triangle ABC $$ 中,$$ D $$ 是 $$ AB $$ 的中点,$$ E $$ 是 $$ BC $$ 的中点,且 $$ DE = 2EF $$。
步骤解析:
1) 设 $$ \overrightarrow{AB} = \mathbf{a} $$,$$ \overrightarrow{AC} = \mathbf{b} $$。
2) 计算 $$ \overrightarrow{AF} $$:
$$ \overrightarrow{AD} = \frac{1}{2}\mathbf{a} $$
$$ \overrightarrow{AE} = \frac{1}{2}(\mathbf{a} + \mathbf{b}) $$
$$ \overrightarrow{DE} = \overrightarrow{AE} - \overrightarrow{AD} = \frac{1}{2}\mathbf{b} $$
$$ \overrightarrow{EF} = \frac{1}{2}\overrightarrow{DE} = \frac{1}{4}\mathbf{b} $$
$$ \overrightarrow{AF} = \overrightarrow{AE} + \overrightarrow{EF} = \frac{1}{2}\mathbf{a} + \frac{1}{2}\mathbf{b} + \frac{1}{4}\mathbf{b} = \frac{1}{2}\mathbf{a} + \frac{3}{4}\mathbf{b} $$
正确答案为 D。
6. 向量化简:
$$ (\overrightarrow{AB} + \overrightarrow{MB}) + (\overrightarrow{BO} + \overrightarrow{BC}) + \overrightarrow{OM} $$
步骤解析:
1) 合并 $$ \overrightarrow{AB} + \overrightarrow{MB} = \overrightarrow{AM} $$。
2) 合并 $$ \overrightarrow{BO} + \overrightarrow{BC} = \overrightarrow{CO} $$。
3) 表达式变为 $$ \overrightarrow{AM} + \overrightarrow{CO} + \overrightarrow{OM} $$。
4) 合并 $$ \overrightarrow{CO} + \overrightarrow{OM} = \overrightarrow{CM} $$。
5) 最终 $$ \overrightarrow{AM} + \overrightarrow{CM} = \overrightarrow{AC} $$。
正确答案为 D。
7. 向量等式验证:
在 $$ \triangle ABC $$ 中,$$ D, E, F $$ 分别是边 $$ AB, BC, CA $$ 的中点。
验证选项:
A. $$ \overrightarrow{DE} + \overrightarrow{DA} = \overrightarrow{EB} $$ 不成立。
B. $$ \overrightarrow{FD} + \overrightarrow{DE} + \overrightarrow{FE} = \overrightarrow{0} $$ 成立。
C. $$ \overrightarrow{FD} + \overrightarrow{DA} = \overrightarrow{FA} $$ 成立。
D. $$ \overrightarrow{DA} + \overrightarrow{DE} = \overrightarrow{FD} $$ 不成立。
正确答案为 B 和 C,但题目可能单选,选 B。
8. 三角形重心条件:
已知 $$ a\overrightarrow{GA} + b\overrightarrow{GB} + c\overrightarrow{GC} = \overrightarrow{0} $$。
步骤解析:
1) 重心性质:$$ \overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = \overrightarrow{0} $$。
2) 对比可得 $$ a = b = c $$,即等边三角形。
3) $$ \angle A = 60^\circ $$。
正确答案为 B。
9. 单位圆向量夹角:
已知 $$ \overrightarrow{CG} = \overrightarrow{CE} + \overrightarrow{CF} $$。
步骤解析:
1) 因为 $$ E, F, G $$ 在单位圆上,$$ |\overrightarrow{CE}| = |\overrightarrow{CF}| = |\overrightarrow{CG}| = 1 $$。
2) 由向量加法,$$ \overrightarrow{CG} $$ 是 $$ \overrightarrow{CE} $$ 和 $$ \overrightarrow{CF} $$ 的和,夹角为 $$ 120^\circ $$。
3) $$ \overrightarrow{FG} $$ 与 $$ \overrightarrow{GE} $$ 的夹角也是 $$ 120^\circ $$。
正确答案为 C。
10. 向量线性组合化简:
$$ 3(2\overrightarrow{a} + \overrightarrow{b}) + 2(4\overrightarrow{a} + 2\overrightarrow{b}) $$
步骤解析:
1) 展开:$$ 6\overrightarrow{a} + 3\overrightarrow{b} + 8\overrightarrow{a} + 4\overrightarrow{b} $$。
2) 合并同类项:$$ 14\overrightarrow{a} + 7\overrightarrow{b} $$。
正确答案为 D。
.jpg)