正确率80.0%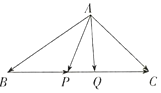 如图所示,$${{P}}$$、$${{Q}}$$是$${{△}{A}{B}{C}}$$的边$${{B}{C}}$$上的两点,且$$\overrightarrow{B P}=\overrightarrow{Q C}$$,则化简$$\overrightarrow{A B}+\overrightarrow{A C}-\overrightarrow{A P}-\overrightarrow{A Q}$$的结果为$${{(}{)}}$$
如图所示,$${{P}}$$、$${{Q}}$$是$${{△}{A}{B}{C}}$$的边$${{B}{C}}$$上的两点,且$$\overrightarrow{B P}=\overrightarrow{Q C}$$,则化简$$\overrightarrow{A B}+\overrightarrow{A C}-\overrightarrow{A P}-\overrightarrow{A Q}$$的结果为$${{(}{)}}$$
A.$${{0}^{→}}$$
B.$$\overrightarrow{B P}$$
C.$$\overrightarrow{P Q}$$
D.$$\overrightarrow{P C}$$
2、['向量减法的定义及运算法则', '向量加法的定义及运算法则', '平面向量基本定理', '向量数乘的定义与运算律']正确率60.0%如图所示,在$${{△}{A}{B}{C}}$$中,$$B D=2 D C$$.若$$\overrightarrow{A B}=\overrightarrow{a}$$,$$\overrightarrow{A C}=\overrightarrow{b}$$,则$$\overrightarrow{A D}=$$()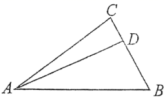
C
A.$$\frac{2} {3} \overrightarrow{a}+\frac{1} {3} \overrightarrow{b}$$
B.$$\frac{2} {3} \overrightarrow{a}-\frac{1} {3} \overrightarrow{b}$$
C.$$\frac{1} {3} \overrightarrow{a}+\frac{2} {3} \overrightarrow{b}$$
D.$$\frac{1} {3} \overrightarrow{a}-\frac{2} {3} \overrightarrow{b}$$
3、['向量加法的定义及运算法则', '向量减法的定义及运算法则']正确率60.0%在平行四边形$${{A}{B}{C}{D}}$$中,设$$\overrightarrow{A B}=\overrightarrow{a}, \, \, \overrightarrow{A D}=\overrightarrow{b}, \, \, \overrightarrow{A C}=\overrightarrow{c}, \, \, \overrightarrow{B D}=\overrightarrow{d},$$下列等式中不正确的是()
B
A.$$\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{c}$$
B.$$\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{d}$$
C.$$\overrightarrow{b}-\overrightarrow{a}=\overrightarrow{d}$$
D.$$\overrightarrow{c}-\overrightarrow{a}=\overrightarrow{b}$$
4、['向量加法的运算律', '向量加法的定义及运算法则', '向量减法的定义及运算法则']正确率19.999999999999996%点$${{G}}$$为$${{△}{A}{B}{C}}$$的重心,设$$\overrightarrow{B G}=\overrightarrow{a}, \, \, \, \overrightarrow{G C}=\overrightarrow{b},$$则$$\overrightarrow{A B}=($$)
C
A.$$\frac{3} {2} \overrightarrow{a}-\frac{1} {2} \overrightarrow{b}$$
B.$$\frac{3} {2} \overrightarrow{a}+\frac{1} {2} \overrightarrow{b}$$
C.$$\vec{b}-2 \vec{a}$$
D.$${{2}{{a}^{→}}{+}{{b}^{→}}}$$
5、['向量加法的运算律', '向量减法的定义及运算法则', '三角形的面积(公式)', '利用基本不等式求最值']正确率40.0%设$${{D}}$$为$${{Δ}{A}{B}{C}}$$的边$${{A}{B}}$$上一点,$${{P}}$$为$${{Δ}{A}{B}{C}}$$内一点,且满足$$\overrightarrow{A D}=\frac{\lambda+1} {\lambda^{2}+2} \overrightarrow{A B}, \, \, \, \overrightarrow{A P}=\overrightarrow{A D}+\frac{\lambda} {\lambda+1} \overrightarrow{B C}, \, \, \lambda> 0.$$则$$\frac{S_{\Delta A P D}} {S_{\Delta A B C}}$$的最大值为()
B
A.$${{2}{\sqrt {2}}}$$$${}$$
B.$$\frac{\sqrt2} {4}$$
C.$$\frac{\sqrt2} {2}$$
D.$${\sqrt {2}}$$
6、['向量加法的定义及运算法则', '向量减法的定义及运算法则']正确率60.0%已知$$O, \, \, M, \, \, A, \, \, B, \, \, C, \, \, D$$是同一平面不同的点,下列各式
A
A.$$\overrightarrow{M B}+\overrightarrow{A D}-\overrightarrow{B M}$$
B.$$( \overrightarrow{A B}+\overrightarrow{C D} )+\overrightarrow{B C}$$
C.$$( \overrightarrow{A D}+\overrightarrow{M B} )+( \overrightarrow{B C}+\overrightarrow{C M} )$$
D.$$- \overrightarrow{O A}+\overrightarrow{O C}+\overrightarrow{C D}$$
7、['向量加法的定义及运算法则', '向量减法的定义及运算法则', '平面向量基本定理']正确率60.0%在平行四边形$${{A}{B}{C}{D}}$$中,对角线$${{A}{C}}$$与$${{B}{D}}$$交于点$${{O}}$$,且$$A E=2 E O,$$则$${{E}{D}{=}{(}}$$)
D
A.$$\frac{2} {3} A D-\frac{1} {3} A B$$
B.$$\frac{2} {3} A D+\frac{1} {3} A B$$
C.$$\frac{1} {3} A D-\frac{2} {3} A B$$
D.$$\frac{1} {3} A D+\frac{2} {3} A B$$
8、['向量加法的定义及运算法则', '向量减法的定义及运算法则', '向量的数量积的定义']正确率60.0%如图,梯形$${{A}{B}{C}{D}}$$中,$$A B / / C D, \, \, \, A B=4, \, \, \, A D=3, \, \, \, C D=2, \, \, \, \angle B A D=6 0^{\circ}$$,则$$\overrightarrow{A B} \cdot\overrightarrow{B C}=\emptyset$$)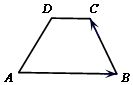
C
A.$${{2}}$$
B.$${{6}}$$
C.$${{−}{2}}$$
D.$${{−}{6}}$$
9、['向量加法的定义及运算法则', '向量减法的定义及运算法则']正确率60.0%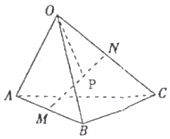 已知三棱锥$$O-A B C$$
已知三棱锥$$O-A B C$$
D
A.$$\frac1 6 \overrightarrow{a}+\frac1 6 \overrightarrow{b}-\frac1 3 \overrightarrow{c}$$
B.$$\frac{1} {6} \overrightarrow{a}+\frac{1} {3} \overrightarrow{a}+\frac{1} {6} \overrightarrow{c}$$
C.$$\frac{1} {3} \overrightarrow{a}+\frac{1} {6} \overrightarrow{b}+\frac{1} {6} \overrightarrow{c}$$
D.$$\frac{1} {6} \overrightarrow{a}+\frac{1} {6} \overrightarrow{b}+\frac{1} {3} \overrightarrow{c}$$
10、['向量加法的定义及运算法则', '向量减法的定义及运算法则', '向量数乘的定义与运算律']正确率60.0%在$$- O A C B$$中,$${{E}}$$是$${{A}{C}}$$的中点,$${{F}}$$是$${{B}{C}}$$上的一点,且$$B C=\lambda B F$$.若$$\bar{O C}=\frac{6} {7} \bar{O E}+\frac{4} {7} \bar{O F},$$则实数$${{λ}{=}{(}{)}}$$
C
A.$${{2}}$$
B.$${{3}}$$
C.$${{4}}$$
D.$${{5}}$$
1. 解析:
2. 解析:
3. 解析:
4. 解析:
5. 解析:
6. 解析:
7. 解析:
8. 解析:
9. 解析:
10. 解析:
.jpg)