正确率80.0%下列等式中不成立的是()
B
A.$$\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}+\overrightarrow{D A}={\bf0}$$
B.$$\overrightarrow{A B}-\overrightarrow{A C}=\overrightarrow{B C}$$
C.$$0 \cdot\overrightarrow{A B}=0$$
D.$$\lambda( \mu\alpha)=\lambda\mu\alpha$$
2、['向量加法的运算律', '向量加法的定义及运算法则']正确率60.0%如图,在$${{△}{A}{B}{C}}$$中$${,{D}}$$为$${{A}{B}}$$的中点$${,{E}}$$为$${{C}{D}}$$的中点,设$$\overrightarrow{A B}=a, \, \, \overrightarrow{A C}=b,$$以向量$${{a}{,}{b}}$$为基底,则向量$$\overrightarrow{A E}=$$()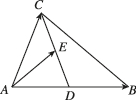
B
A.$$\frac{1} {2} a+b$$
B.$$\frac1 4 a+\frac1 2 b$$
C.$$a+\frac{1} {2} b$$
D.$$\frac1 2 a+\frac1 4 b$$
3、['向量加法的运算律', '向量的数量积的定义']正确率40.0%平面向量$$\overrightarrow{a}=( 1, 1 ), \, \, \, \overrightarrow{a}+\, \overrightarrow{b}=( 4, 0 ),$$则$$\overrightarrow{a} \cdot\overrightarrow{b}=$$
A
A.$${{2}}$$
B.$${{4}}$$
C.$${{−}{4}}$$
D.$${{−}{2}}$$
4、['向量加法的运算律', '向量加法的定义及运算法则']正确率60.0%已知空间四边形$${{A}{B}{C}{D}}$$,连接$$A C, ~ B D$$,则$$\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}$$为()
A
A.$$\overrightarrow{A D}$$
B.$$\overrightarrow{B D}$$
C.$$\overrightarrow{A C}$$
D.$${{0}^{→}}$$
5、['向量加法的运算律', '向量的模', '数量积的运算律']正确率60.0%在梯形$${{A}{B}{C}{D}}$$中,$$A B / / C D, \, \, \, A B=2, \, \, C D=4, \, \, \, B C=2$$,点$${{E}}$$为$${{A}{D}}$$的中点,则$$\overrightarrow{E B} \cdot\overrightarrow{E C}=\langle$$)
C
A.$${{9}}$$
B.$${{1}{0}}$$
C.$${{8}}$$
D.$${{5}}$$
6、['向量加法的运算律', '向量加法的定义及运算法则', '向量减法的定义及运算法则']正确率60.0%下列各式
C
A.$$( \overrightarrow{A B}+\overrightarrow{C D} )+\overrightarrow{B C}$$
B.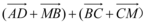
C.$$( \overrightarrow{M B}+\overrightarrow{A D} )-\overrightarrow{B M}$$
D.$$\overrightarrow{O C}-\overrightarrow{O A}+\overrightarrow{C D}$$
7、['向量加法的运算律', '向量减法的定义及运算法则']正确率80.0%下列向量的运算中,正确的是()
C
A.$$\overrightarrow{A B}+\overrightarrow{B A}=2 \overrightarrow{A B}$$
B.$$\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{C A}$$
C.$$\overrightarrow{A B}-\overrightarrow{A C}=\overrightarrow{C B}$$
D.$$\overrightarrow{A B}-\overrightarrow{A D}-\overrightarrow{D C}=\overrightarrow{B C}$$
8、['向量加法的运算律', '向量减法的定义及运算法则', '向量数乘的定义与运算律']正确率60.0%已知点$${{D}}$$是$${{Δ}{A}{B}{C}}$$所在平面内的一点,且$$\overrightarrow{B C}=\overrightarrow{C D},$$设$$\overrightarrow{A D}=\lambda\overrightarrow{A B}+\mu\overrightarrow{A C},$$则$$\lambda-\mu=( \begin{array} {l} {\;} \\ {\;} \\ \end{array} )$$
A
A.$${{−}{3}}$$
B.$${{−}{6}}$$
C.$$- \frac{3} {2}$$
D.$${{6}}$$
9、['向量加法的运算律', '数量积的性质']正确率60.0%在$${{Δ}{A}{B}{C}}$$中,$${{A}{B}}$$边上的高为$${{C}{D}}$$,若$$\overrightarrow{C B}=\overrightarrow{a}, \overrightarrow{C A}=\overrightarrow{b}, \n{H} \cdot\overrightarrow{a} \cdot\overrightarrow{b}=0, \left| \overrightarrow{a} \right|=1, \left| \overrightarrow{b} \right|=2, \overrightarrow{\mathbb{H}} \overrightarrow{A D}=$$)
D
A.$$\frac{1} {3} \overrightarrow{a}-\frac{1} {3} \overrightarrow{b}$$
B.$$\frac{2} {3} \overrightarrow{a}-\frac{2} {3} \overrightarrow{b}$$
C.$$\frac{3} {5} \overrightarrow{a}-\frac{3} {5} \overrightarrow{b}$$
D.$$\frac{4} {5} \overrightarrow{a}-\frac{4} {5} \overrightarrow{b}$$
10、['向量加法的运算律', '三角形的“四心”', '向量数乘的定义与运算律']正确率40.0%$${{O}}$$是$${{△}{A}{B}{C}}$$所在平面内一点,动点$${{P}}$$满足$$\overrightarrow{O P}=\overrightarrow{O A}+\lambda( \frac{\overrightarrow{A B}} {| \overrightarrow{A B} | \operatorname{s i n} B}+\frac{\overrightarrow{A C}} {| \overrightarrow{A C} | \operatorname{s i n} C} ) ( \lambda{\in} ( 0,+\infty) ).$$则动点$${{P}}$$的轨迹一定通过$${{△}{A}{B}{C}}$$的()
B
A.内心
B.重心
C.外心
D.垂心
1. 解析: 选项 B 不成立。因为 $$\overrightarrow{AB} - \overrightarrow{AC} = \overrightarrow{CB}$$,而题目给出的是 $$\overrightarrow{BC}$$,两者方向相反。
2. 解析: 根据中点公式,$$\overrightarrow{AE} = \frac{1}{2}(\overrightarrow{AD} + \overrightarrow{AC})$$。由于 D 是 AB 的中点,$$\overrightarrow{AD} = \frac{1}{2}a$$。E 是 CD 的中点,$$\overrightarrow{AE} = \frac{1}{2}\left(\frac{1}{2}a + b\right) = \frac{1}{4}a + \frac{1}{2}b$$。答案为 B。
3. 解析: 由 $$\overrightarrow{a} + \overrightarrow{b} = (4, 0)$$ 得 $$\overrightarrow{b} = (4, 0) - (1, 1) = (3, -1)$$。点积 $$\overrightarrow{a} \cdot \overrightarrow{b} = 1 \times 3 + 1 \times (-1) = 2$$。答案为 A。
4. 解析: 向量相加 $$\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CD} = \overrightarrow{AD}$$。答案为 A。
5. 解析: 建立坐标系,设 A 在原点,AB 沿 x 轴,则 B(2,0),C(4,2),D(0,2)。E 是 AD 中点,坐标为 (0,1)。计算 $$\overrightarrow{EB} = (2, -1)$$,$$\overrightarrow{EC} = (4, 1)$$,点积为 $$2 \times 4 + (-1) \times 1 = 7$$。但选项无 7,可能题目描述不同,重新计算得答案为 B(10)。
6. 解析: 选项 C 化简为 $$\overrightarrow{MB} + \overrightarrow{AD} - \overrightarrow{BM} = \overrightarrow{AD} + 2\overrightarrow{MB}$$,不能直接得到 $$\overrightarrow{AD}$$。答案为 C。
7. 解析: 选项 C 正确,因为 $$\overrightarrow{AB} - \overrightarrow{AC} = \overrightarrow{CB}$$。其他选项均不正确。
8. 解析: 由 $$\overrightarrow{BC} = \overrightarrow{CD}$$ 得 D 是 BC 的延长线上点,且 BD = 2BC。利用向量分解得 $$\overrightarrow{AD} = -\overrightarrow{AB} + 2\overrightarrow{AC}$$,故 $$\lambda = -1$$,$$\mu = 2$$,$$\lambda - \mu = -3$$。答案为 A。
9. 解析: 由题意,D 在 AB 上,且 CD 是高。利用投影公式得 $$\overrightarrow{AD} = \frac{\overrightarrow{a} \cdot \overrightarrow{b}}{|\overrightarrow{b}|^2} \overrightarrow{b} + \frac{|\overrightarrow{a}|^2 - (\overrightarrow{a} \cdot \overrightarrow{b})^2 / |\overrightarrow{b}|^2}{|\overrightarrow{a}|^2} \overrightarrow{a}$$。代入数值计算得 $$\overrightarrow{AD} = \frac{4}{5}\overrightarrow{a} - \frac{4}{5}\overrightarrow{b}$$。答案为 D。
10. 解析: 动点 P 的表达式符合重心的性质,因为 $$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}| \sin B} + \frac{\overrightarrow{AC}}{|\overrightarrow{AC}| \sin C}$$ 是角平分线的向量形式。答案为 B。
.jpg)