.jpg)
正确率80.0%下列等式中不成立的是（）
B
A.$$\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}+\overrightarrow{D A}={\bf0}$$
B.$$\overrightarrow{A B}-\overrightarrow{A C}=\overrightarrow{B C}$$
C.$$0 \cdot\overrightarrow{A B}=0$$
D.$$\lambda( \mu\alpha)=\lambda\mu\alpha$$
2、['向量加法的定义及运算法则'， '向量减法的定义及运算法则'， '向量数乘的定义与运算律']正确率40.0%在$${{△}{A}{B}{C}}$$中，若点$${{D}}$$满足$$\overrightarrow{B D}=2 \overrightarrow{D C}，$$则$$\overrightarrow{A D}=($$）
D
A.$$\frac{1} {3} \overrightarrow{A C}+\frac{2} {3} \overrightarrow{A B}$$
B.$$\frac{5} {3} \overrightarrow{A B}-\frac{2} {3} \overrightarrow{A C}$$
C.$$\frac{2} {3} \overrightarrow{A C}-\frac{1} {3} \overrightarrow{A B}$$
D.$$\frac2 3 \overrightarrow{A C}+\frac1 3 \overrightarrow{A B}$$
3、['向量的模'， '平面向量的概念'， '向量数乘的定义与运算律']正确率60.0%有下列命题：$${①}$$若$${{a}^{→}}$$与$${{b}^{→}}$$是非零向量，则$$( \overrightarrow{a}+\overrightarrow{b} ) \cdot( \overrightarrow{a}-\overrightarrow{b} )=0 \Leftrightarrow| \overrightarrow{a} |=| \overrightarrow{b} | ; \; \textcircled{}$$若$$\overrightarrow{a} \cdot\overrightarrow{b}=\overrightarrow{b} \cdot\overrightarrow{c}$$且$$\overrightarrow{b} \neq\overrightarrow{0}，$$则$$\overrightarrow{a}=\overrightarrow{c} ;$$若$$\overrightarrow{a} / / \overrightarrow{b}， \ \overrightarrow{b} / / \overrightarrow{c}，$$则$$\overrightarrow{a} / / \overrightarrow{c}， \， \， \oplus\overrightarrow{a} \cdot( \overrightarrow{b} \cdot\overrightarrow{c} )=( \overrightarrow{a} \cdot\overrightarrow{b} ) \cdot\overrightarrow{c}，$$其中正确命题的个数为（）
B
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
4、['向量加法的定义及运算法则'， '向量减法的定义及运算法则'， '平面向量基本定理'， '向量数乘的定义与运算律']正确率60.0%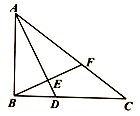
如图，$${{△}{A}{B}{C}}$$
A
A.$${\frac{1} {2}} \overrightarrow{A B}+{\frac{3} {1 0}} \overrightarrow{A C}$$
B.$$\frac{1} {2} \overrightarrow{A B}+\frac{1} {3} \overrightarrow{A C}$$
C.$$\frac{2} {5} \overrightarrow{A B}+\frac{3} {1 0} \overrightarrow{A C}$$
D.$$\frac{2} {5} \overrightarrow{A B}+\frac{1} {3} \overrightarrow{A C}$$
5、['向量加法的定义及运算法则'， '向量减法的定义及运算法则'， '向量数乘的定义与运算律']正确率60.0%已知向量$$\overrightarrow{O A}=\overrightarrow{a}， \overrightarrow{O B}=\overrightarrow{b}， \overrightarrow{O C}=\overrightarrow{c}，$$且$$\overrightarrow{A C}=-4 \overrightarrow{C B}，$$则$${{(}{)}}$$
D
A.$$\overrightarrow{c}=\frac{1} {2} \overrightarrow{a}+\frac{3} {2} \overrightarrow{b}$$
B.$$\overrightarrow{c}=\frac{3} {2} \overrightarrow{a}-\frac{1} {2} \overrightarrow{b}$$
C.$$\overrightarrow{c}=\frac{1} {2} \overrightarrow{a}-\frac{3} {2} \overrightarrow{b}$$
D.$$\overrightarrow{c}=-\frac{1} {3} \overrightarrow{a}+\frac{4} {3} \overrightarrow{b}$$
6、['向量数乘的定义与运算律']正确率60.0%已知向量$${{a}{⃗}}$$与$${{b}^{⃗}}$$反向，且$$\left\vert\vec{a} \right\vert=r， \， \， \， \left\vert\vec{b} \right\vert=R， \， \， \， \vec{b}=\lambda\vec{a}，$$则$${{λ}}$$的值等于$${{(}{)}}$$
C
A.$$\frac{r} {R}$$
B.$$- \frac{r} {R}$$
C.$$- \frac{R} {r}$$
D.$$\frac{R} {r}$$
7、['向量加法的定义及运算法则'， '向量数乘的定义与运算律']正确率60.0%已知空间四边形$${{A}{B}{C}{D}}$$的对角线为$$A C， ~ B D， ~ G$$是$${{C}{D}}$$的中点，则$$\overrightarrow{A B}+\frac{1} {2} ( \overrightarrow{B D}+\overrightarrow{B C} )=$$
A
A.$${{A}{G}^{⇀}}$$
B.$${{C}{G}^{⇀}}$$
C.$${{B}{C}^{⇀}}$$
D.$${\frac{1} {2}} \overrightarrow{B C}$$
8、['双曲线的离心率'， '向量垂直'， '向量数乘的定义与运算律'， '双曲线的顶点、长轴、短轴、焦点、焦距'， '双曲线的对称性'， '双曲线的定义']正确率40.0%设$${{F}_{1}{，}{{F}_{2}}}$$为双曲线$$C : \frac{x^{2}} {a^{2}}-\frac{y^{2}} {b^{2}}=1$$的左，右焦点，$${{P}{，}{Q}}$$为双曲线$${{C}}$$右支上的两点，若$$\overrightarrow{P F_{2}}=2 \overrightarrow{F_{2} Q}，$$且$$\overrightarrow{F_{1} Q} \cdot\overrightarrow{P Q}=0，$$则该双曲线的离心率是$${{(}{)}}$$
B
A.$$\frac{\sqrt{1 5}} {3}$$
B.$$\frac{\sqrt{1 7}} {3}$$
C.$$\frac{\sqrt5} {2}$$
D.$$\frac{\sqrt{7}} {2}$$
9、['数量积的性质'， '向量数乘的定义与运算律'， '命题的真假性判断']正确率60.0%对于向量$$\rightharpoonup， ~ \overrightarrow{b}， ~ \overrightarrow{c}$$和实数$${{λ}{，}}$$下列命题中正确的是（）
B
A.若$$\rightharpoonup\cdot\overrightarrow{b}=0，$$则$${{a}^{⇀}{=}{{0}^{⇀}}}$$或$${{b}^{⇀}{=}{{0}^{⇀}}}$$
B.若$$\lambda\rightharpoonup=\overrightarrow{0}，$$则$${{λ}{=}{0}}$$或$${{a}^{⇀}{=}{{0}^{⇀}}}$$
C.若$$\overrightarrow{a}^{2}=\overrightarrow{b}^{2}$$，则$${{a}^{⇀}{=}{{b}^{⇀}}}$$或$$\overrightarrow{a}=-\overrightarrow{b}$$
D.若$$\overrightarrow{a} \cdot\overrightarrow{b}=\overrightarrow{a} \cdot\overrightarrow{c}，$$则$${{b}^{⇀}{=}{{c}^{⇀}}}$$
10、['向量加法的定义及运算法则'， '向量减法的定义及运算法则'， '平面向量基本定理'， '向量数乘的定义与运算律'， '向量的线性运算']正确率60.0%如图在平行四边形$${{A}{B}{C}{D}}$$中，对角线$${{A}{C}}$$与$${{B}{D}}$$交于点$${{O}}$$，且$$\overrightarrow{A E}=2 \overrightarrow{E O}，$$则$$\overrightarrow{E D}=($$）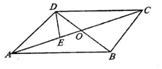
C
A.$$\frac{1} {3} \overrightarrow{A D}-\frac{2} {3} \overrightarrow{A B}$$
B.$$\frac{2} {3} \overrightarrow{A D}+\frac{1} {3} \overrightarrow{A B}$$
C.$$\frac{2} {3} \overrightarrow{A D}-\frac{1} {3} \overrightarrow{A B}$$
D.$$\frac{1} {3} \overrightarrow{A D}+\frac{2} {3} \overrightarrow{A B}$$
1. 解析： 选项B不成立。因为 $$\overrightarrow{AB} - \overrightarrow{AC} = \overrightarrow{CB}$$，而题目中给出的是 $$\overrightarrow{BC}$$，两者方向相反，故B错误。其他选项A、C、D均成立。
2. 解析： 根据题意，点D将BC分为2:1的比例，因此 $$\overrightarrow{AD} = \frac{2}{3}\overrightarrow{AC} + \frac{1}{3}\overrightarrow{AB}$$，对应选项D。
3. 解析： 命题①正确，因为 $$(\overrightarrow{a}+\overrightarrow{b}) \cdot (\overrightarrow{a}-\overrightarrow{b}) = |\overrightarrow{a}|^2 - |\overrightarrow{b}|^2 = 0 \Leftrightarrow |\overrightarrow{a}| = |\overrightarrow{b}|$$；命题②错误，因为向量点积不满足消去律；命题③错误，若 $$\overrightarrow{b} = \overrightarrow{0}$$，则 $$\overrightarrow{a}$$ 和 $$\overrightarrow{c}$$ 不一定平行；命题④错误，因为 $$(\overrightarrow{a} \cdot \overrightarrow{b}) \cdot \overrightarrow{c}$$ 是标量乘向量，而 $$\overrightarrow{a} \cdot (\overrightarrow{b} \cdot \overrightarrow{c})$$ 无意义。故只有1个正确命题，选B。
4. 解析： 题目缺少图形描述，无法直接解析。通常此类题目需根据向量分解或比例关系求解，但选项未明确对应条件。
5. 解析： 由 $$\overrightarrow{AC} = -4\overrightarrow{CB}$$，可得 $$\overrightarrow{c} - \overrightarrow{a} = -4(\overrightarrow{b} - \overrightarrow{c})$$，解得 $$\overrightarrow{c} = \frac{1}{3}\overrightarrow{a} + \frac{4}{3}\overrightarrow{b}$$，对应选项D。
6. 解析： 向量 $$\overrightarrow{a}$$ 与 $$\overrightarrow{b}$$ 反向且 $$\overrightarrow{b} = \lambda \overrightarrow{a}$$，则 $$\lambda = -\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|} = -\frac{R}{r}$$，选C。
7. 解析： 表达式化简为 $$\overrightarrow{AB} + \frac{1}{2}(\overrightarrow{BD} + \overrightarrow{BC}) = \overrightarrow{AB} + \overrightarrow{BG} = \overrightarrow{AG}$$（G为CD中点），选A。
8. 解析： 根据双曲线性质及向量条件，通过几何关系和离心率定义可推导出离心率为 $$\frac{\sqrt{17}}{3}$$，选B。
9. 解析： 选项B正确，因为 $$\lambda \overrightarrow{a} = \overrightarrow{0}$$ 时，$$\lambda = 0$$ 或 $$\overrightarrow{a} = \overrightarrow{0}$$。其他选项A、C、D均不成立。
10. 解析： 在平行四边形中，$$\overrightarrow{ED} = \overrightarrow{AD} - \overrightarrow{AE}$$。由 $$\overrightarrow{AE} = 2\overrightarrow{EO}$$ 可得 $$\overrightarrow{AE} = \frac{2}{3}\overrightarrow{AO} = \frac{1}{3}\overrightarrow{AC} = \frac{1}{3}(\overrightarrow{AB} + \overrightarrow{AD})$$，因此 $$\overrightarrow{ED} = \overrightarrow{AD} - \frac{1}{3}(\overrightarrow{AB} + \overrightarrow{AD}) = \frac{2}{3}\overrightarrow{AD} - \frac{1}{3}\overrightarrow{AB}$$，选C。