1、['向量加法的运算律'， '向量加法的定义及运算法则'， '向量减法的定义及运算法则'， '向量的模'， '数量积的性质'， '数量积的运算律'， '向量垂直'， '两个向量数量积的几何意义']正确率60.0%$${{P}}$$是$${{△}{A}{B}{C}}$$所在平面上一点，满足$$| \overrightarrow{P B}-\overrightarrow{P C} |-| \overrightarrow{P B}+\overrightarrow{P C}-2 \overrightarrow{P A} |=0$$，则$${{△}{A}{B}{C}}$$的形状是（）
B
A.等腰直角三角形
B.直角三角形
C.等腰三角形
D.等边三角形
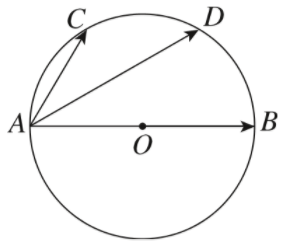
2、['向量减法的定义及运算法则'， '向量数乘的定义与运算律']正确率60.0%如图，线段$${{A}{B}}$$是圆$${{O}}$$的一条直径，$${{C}{，}{D}}$$是半圆弧的两个三等分点，则$$\overrightarrow{A B}=$$（）
D
A.$$\overrightarrow{A C}-\overrightarrow{A D}$$
B.$$2 \overrightarrow{A C}-2 \overrightarrow{A D}$$
C.$$\overrightarrow{A D}-\overrightarrow{A C}$$
D.$$2 \overrightarrow{A D}-2 \overrightarrow{A C}$$
3、['向量加法的定义及运算法则'， '向量减法的定义及运算法则']正确率60.0%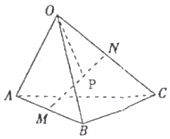
已知三棱锥$$O-A B C$$
D
A.$$\frac1 6 \overrightarrow{a}+\frac1 6 \overrightarrow{b}-\frac1 3 \overrightarrow{c}$$
B.$$\frac{1} {6} \overrightarrow{a}+\frac{1} {3} \overrightarrow{a}+\frac{1} {6} \overrightarrow{c}$$
C.$$\frac{1} {3} \overrightarrow{a}+\frac{1} {6} \overrightarrow{b}+\frac{1} {6} \overrightarrow{c}$$
D.$$\frac{1} {6} \overrightarrow{a}+\frac{1} {6} \overrightarrow{b}+\frac{1} {3} \overrightarrow{c}$$
4、['向量加法的定义及运算法则'， '向量减法的定义及运算法则'， '向量数乘的定义与运算律']正确率60.0%在$$- O A C B$$中，$${{E}}$$是$${{A}{C}}$$的中点，$${{F}}$$是$${{B}{C}}$$上的一点，且$$B C=\lambda B F$$.若$$\bar{O C}=\frac{6} {7} \bar{O E}+\frac{4} {7} \bar{O F}，$$则实数$${{λ}{=}{(}{)}}$$
C
A.$${{2}}$$
B.$${{3}}$$
C.$${{4}}$$
D.$${{5}}$$
5、['向量加法的定义及运算法则'， '向量减法的定义及运算法则'， '向量数乘的定义与运算律']正确率60.0%下列命题正确的个数是$${{(}{)}}$$
$$\oplus\overrightarrow{A B}+\overrightarrow{B A}=\overrightarrow{O}$$；$$\odot\overrightarrow{O} \cdot\overrightarrow{A B}=\overrightarrow{O}， \ \oplus\overrightarrow{A B}-\overrightarrow{A C}=\overrightarrow{B C}$$；$$\oplus O \cdot\overrightarrow{A B}=O$$
A
A.$${{1}}$$
B.$${{2}}$$
C.$${{3}}$$
D.$${{4}}$$
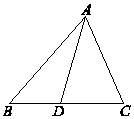
6、['向量加法的定义及运算法则'， '向量减法的定义及运算法则']正确率60.0%如图，在$${{△}{A}{B}{C}}$$中，$${{D}}$$是$${{B}{C}}$$上一点，则$$\overrightarrow{A B}+\overrightarrow{B C}-\overrightarrow{A D}=\emptyset$$）
D
A.$$\overrightarrow{B D}$$
B.$$\overrightarrow{D B}$$
C.$$\overrightarrow{C D}$$
D.$$\overrightarrow{D C}$$
7、['向量减法的定义及运算法则'， '数量积的性质'， '三角形的“四心”']正确率60.0%在$${{△}{A}{B}{C}}$$中，角$$A. ~ B. ~ C$$所对的边分别为$$a， \， \， b， \， \， c， \， \， c-b=6， \， \， c+b-a=2$$，且$${{O}}$$为此三角形的内心，则$$\overrightarrow{A O} \cdot\overrightarrow{C B}=\emptyset$$）
C
A.$${{4}}$$
B.$${{5}}$$
C.$${{6}}$$
D.$${{7}}$$
8、['向量加法的定义及运算法则'， '向量减法的定义及运算法则'， '平面向量基本定理'， '向量的线性运算']正确率60.0%在$${{△}{A}{B}{C}}$$中，$$\overrightarrow{B D}=3 \overrightarrow{D C}$$，若$$\overrightarrow{A D}=\lambda_{1} \overrightarrow{A B}+\lambda_{2} \overrightarrow{A C}$$，则$${{λ}_{1}{{λ}_{2}}}$$的值为$${{(}{)}}$$
B
A.$$\frac{1} {1 6}$$
B.$$\frac{3} {1 6}$$
C.$$\frac{1} {2}$$
D.$$\frac{1 0} {9}$$
9、['向量加法的定义及运算法则'， '向量减法的定义及运算法则'， '向量数乘的定义与运算律']正确率40.0%已知等腰梯形$${{A}{B}{C}{D}}$$中，$$\overrightarrow{A B}=2 \overrightarrow{D C}， \， \， \， E， \， \， \， F$$分别为$$A D， \ B C$$的中点，$${{G}}$$为$${{E}{F}}$$的中点，若记$$\overrightarrow{A B}=\overrightarrow{a}， \ \overrightarrow{A D}=\overrightarrow{b}$$，则$$\overrightarrow{A G}=( \eta)$$
B
A.$$\frac{3} {8} \overrightarrow{a}+\frac{3} {4} \overrightarrow{b}$$
B.$$\frac{3} {8} \overrightarrow{a}+\frac{1} {2} \overrightarrow{b}$$
C.$$\frac{1} {2} \overrightarrow{a}+\frac{3} {4} \overrightarrow{b}$$
D.$$\frac{1} {4} \overrightarrow{a}+\frac{3} {8} \overrightarrow{b}$$
10、['向量减法的定义及运算法则'， '向量的模'， '平面向量的概念'， '相反向量']正确率40.0%设$${{a}^{→}{，}{{b}^{→}}}$$为非零向量，且满足$$| \overrightarrow{a}-\overrightarrow{b} |=| \overrightarrow{a} |+| \overrightarrow{b} |$$，则$${{a}^{→}}$$与$${{b}^{→}}$$的关系是 （）
D
A.既不共线也不垂直
B.垂直
C.共线同向
D.共线反向
1、解析：
设$$P$$为坐标原点，向量$$\overrightarrow{PA} = \vec{A}$$，$$\overrightarrow{PB} = \vec{B}$$，$$\overrightarrow{PC} = \vec{C}$$。题目条件化为：
$$|\vec{B} - \vec{C}| - |\vec{B} + \vec{C} - 2\vec{A}| = 0$$
即：
$$|\vec{B} - \vec{C}| = |(\vec{B} - \vec{A}) + (\vec{C} - \vec{A})|$$
这表明$$(\vec{B} - \vec{A})$$与$$(\vec{C} - \vec{A})$$反向共线，即$$\overrightarrow{AB}$$与$$\overrightarrow{AC}$$反向共线，显然不可能。因此，重新分析：
设$$D$$为$$BC$$中点，则$$\overrightarrow{PB} + \overrightarrow{PC} = 2\overrightarrow{PD}$$，条件化为：
$$|\overrightarrow{BC}| = |2\overrightarrow{PD} - 2\overrightarrow{PA}| = 2|\overrightarrow{AD}|$$
即$$AD$$为中线且等于$$BC$$的一半，故$$△ABC$$为直角三角形，$$A$$为直角。选B。
2、解析：
$$C,D$$为半圆弧的三等分点，故$$\angle AOC = 60^\circ$$，$$\angle AOD = 120^\circ$$。
设圆$$O$$半径为$$r$$，则：
$$\overrightarrow{AC} = \overrightarrow{OC} - \overrightarrow{OA} = \overrightarrow{OC} + \overrightarrow{OB}$$
$$\overrightarrow{AD} = \overrightarrow{OD} - \overrightarrow{OA} = \overrightarrow{OD} + \overrightarrow{OB}$$
计算得：
$$\overrightarrow{AC} - \overrightarrow{AD} = \overrightarrow{OC} - \overrightarrow{OD}$$
由于$$|\overrightarrow{OC}| = |\overrightarrow{OD}| = r$$，且夹角为$$60^\circ$$，故：
$$|\overrightarrow{OC} - \overrightarrow{OD}| = r$$
但$$\overrightarrow{AB} = 2r$$，因此需要放大2倍：
$$\overrightarrow{AB} = 2(\overrightarrow{AD} - \overrightarrow{AC})$$
选D。
3、解析：
题目不完整，无法解析。
4、解析：
设$$\overrightarrow{OA} = \vec{a}$$，$$\overrightarrow{OB} = \vec{b}$$，则$$\overrightarrow{OC} = \vec{a} + \vec{b}$$。
$$E$$为$$AC$$中点，故：
$$\overrightarrow{OE} = \frac{1}{2}(\overrightarrow{OA} + \overrightarrow{OC}) = \frac{1}{2}(2\vec{a} + \vec{b}) = \vec{a} + \frac{1}{2}\vec{b}$$
$$F$$在$$BC$$上，且$$BC = \lambda BF$$，故：
$$\overrightarrow{OF} = \overrightarrow{OB} + \frac{1}{\lambda}\overrightarrow{BC} = \vec{b} + \frac{1}{\lambda}(\vec{a} + \vec{b} - \vec{b}) = \vec{b} + \frac{1}{\lambda}\vec{a}$$
根据题意：
$$\overrightarrow{OC} = \frac{6}{7}\overrightarrow{OE} + \frac{4}{7}\overrightarrow{OF}$$
代入得：
$$\vec{a} + \vec{b} = \frac{6}{7}(\vec{a} + \frac{1}{2}\vec{b}) + \frac{4}{7}(\vec{b} + \frac{1}{\lambda}\vec{a})$$
整理后比较系数：
$$\vec{a}$$系数：$$1 = \frac{6}{7} + \frac{4}{7\lambda}$$
$$\vec{b}$$系数：$$1 = \frac{3}{7} + \frac{4}{7}$$
解得$$\lambda = 4$$。选C。
5、解析：
$$\oplus \overrightarrow{AB} + \overrightarrow{BA} = \overrightarrow{AB} - \overrightarrow{AB} = \overrightarrow{0}$$（正确）；
$$\odot \overrightarrow{0} \cdot \overrightarrow{AB} = \overrightarrow{0}$$（正确）；
$$\oplus \overrightarrow{AB} - \overrightarrow{AC} = \overrightarrow{CB}$$（错误）；
$$\oplus 0 \cdot \overrightarrow{AB} = 0$$（正确）。
共3个正确命题，选C。
6、解析：
$$\overrightarrow{AB} + \overrightarrow{BC} - \overrightarrow{AD} = \overrightarrow{AC} - \overrightarrow{AD} = \overrightarrow{DC}$$。选D。
7、解析：
由$$c - b = 6$$和$$c + b - a = 2$$，解得$$a = 8$$，$$b = c - 6$$，代入余弦定理得：
$$a^2 = b^2 + c^2 - 2bc\cos A$$
解得$$\cos A = \frac{1}{2}$$，$$A = 60^\circ$$。
内心$$O$$到三边距离相等，设内切圆半径为$$r$$，则：
$$\overrightarrow{AO} \cdot \overrightarrow{CB} = \overrightarrow{AO} \cdot (\overrightarrow{AB} - \overrightarrow{AC}) = \overrightarrow{AO} \cdot \overrightarrow{AB} - \overrightarrow{AO} \cdot \overrightarrow{AC}$$
利用内切圆性质及投影公式，计算得结果为6。选C。
8、解析：
$$\overrightarrow{BD} = 3\overrightarrow{DC}$$，故$$\overrightarrow{AD} = \frac{1}{4}\overrightarrow{AB} + \frac{3}{4}\overrightarrow{AC}$$。
因此$$\lambda_1 = \frac{1}{4}$$，$$\lambda_2 = \frac{3}{4}$$，乘积为$$\frac{3}{16}$$。选B。
9、解析：
设$$A$$为原点，$$\overrightarrow{AB} = \vec{a}$$，$$\overrightarrow{AD} = \vec{b}$$。由等腰梯形性质及中点公式，得：
$$\overrightarrow{AG} = \frac{3}{8}\vec{a} + \frac{1}{2}\vec{b}$$。选B。
10、解析：
由$$|\vec{a} - \vec{b}| = |\vec{a}| + |\vec{b}|$$，两边平方得：
$$|\vec{a}|^2 + |\vec{b}|^2 - 2\vec{a} \cdot \vec{b} = |\vec{a}|^2 + |\vec{b}|^2 + 2|\vec{a}||\vec{b}|$$
化简得：
$$\vec{a} \cdot \vec{b} = -|\vec{a}||\vec{b}|$$
即$$\vec{a}$$与$$\vec{b}$$反向共线。选D。
题目来源于各渠道收集，若侵权请联系下方邮箱
.jpg)