正确率40.0%给出以下命题:$${①}$$若$$| \overrightarrow{a}+\overrightarrow{b} |=| \overrightarrow{a}-\overrightarrow{b} |$$,则$${{a}^{→}}$$与$${{b}^{→}}$$共线;$${②}$$函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) \ =\operatorname{c o s} \left( \begin{matrix} {\operatorname{s i n} x} \\ \end{matrix} \right)$$的最小正周期为$${{π}{;}{③}}$$在$${{△}{A}{B}{C}}$$中,$$| \overrightarrow{A C} |=3, \, \, \, | \overrightarrow{B C} |=4, \, \, \, | \overrightarrow{A B} |=5$$,则$$\overrightarrow{A B} \cdot\overrightarrow{B C}=1 6 ;$$函数$$f \left( \begin{matrix} {x} \\ \end{matrix} \right) \ =\operatorname{t a n} \ ( \begin{matrix} {2 x} \\ {-\frac{\pi} {3}} \\ \end{matrix} )$$的一个对称中心为$$( \frac{5 \pi} {1 2}, \ 0 )$$,其中正确命题的序号为()
A
A.$${②{④}}$$
B.$${①{④}}$$
C.$${②{③}}$$
D.$${①{③}}$$
2、['共线向量基本定理', '平面向量的概念']正确率80.0%已知$$\vec{b}=( 3, 1 )$$,$$\overrightarrow{a}=( x, 3 )$$,且$$\overrightarrow{a} / / \overrightarrow{b}$$,则$${{x}{=}{(}{)}}$$
A.$${{9}}$$
B.$${{−}{9}}$$
C.$${{1}}$$
D.$${{−}{1}}$$
3、['共线向量基本定理', '三角形的“四心”', '三角形的面积(公式)']正确率40.0%设$${{O}}$$为$${{△}{A}{B}{C}}$$所在平面内一点,满足$$2 \overrightarrow{O A}-7 \overrightarrow{O B}-3 \overrightarrow{O C}=0.$$则$${{△}{A}{B}{C}}$$的面积与$${{△}{B}{O}{C}}$$的面积的比值为()
D
A.$${{6}}$$
B.$$\frac{8} {2}$$
C.$$\frac{1 2} {7}$$
D.$${{4}}$$
4、['共线向量基本定理']正确率60.0%在$${{△}{A}{B}{C}}$$中$${,{D}}$$为$${{A}{B}}$$的中点$${,{G}}$$为$${{C}{D}}$$上一点,若$$\overrightarrow{A G}=\frac{1} {3} \overrightarrow{A B}+\lambda\overrightarrow{A C},$$则$${{λ}}$$的值为()
B
A.$$\frac{1} {6}$$
B.$$\frac{1} {3}$$
C.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
D.$$\frac{5} {6}$$
5、['余弦定理及其应用', '共线向量基本定理', '数量积的运算律', '向量的数量积的定义', '向量的线性运算']正确率40.0%如图,已知等腰$${{△}{A}{B}{C}}$$中,$$A B=A C=3$$,$${{B}{C}{=}{4}}$$,点$${{P}}$$是边$${{B}{C}}$$上的动点,则$$\overrightarrow{A P} \cdot( \overrightarrow{A B}+\overrightarrow{A C} )$$()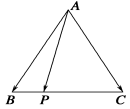
A
A.为定值$${{1}{0}}$$
B.为定值$${{6}}$$
C.最大值为$${{1}{8}}$$
D.与$${{P}}$$的位置有关
6、['共线向量基本定理', '平面向量基本定理']正确率60.0%如图,在$${{△}{A}{B}{C}}$$中,$$\overrightarrow{A N}=\frac{1} {3} \overrightarrow{A C}, \, \, P$$是$${{B}{N}}$$上的一点,若$$m \overrightarrow{A C}=\overrightarrow{A P}-\frac{2} {3} \overrightarrow{A B}$$,则实数$${{m}}$$的值为()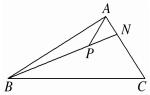
B
A.$$\frac{1} {3}$$
B.$$\begin{array} {l l} {\frac{1} {9}} \\ \end{array}$$
C.$${{1}}$$
D.$${{2}}$$
7、['共线向量基本定理', '向量的线性运算']正确率40.0%如图,一直线$${{E}{F}}$$与平行四边形$${{A}{B}{C}{D}}$$的两边$$A B, ~ A D$$分别交于$${{E}{,}{F}}$$两点,且交其对角线于$${{K}}$$,其中,$$\overrightarrow{A E}=\frac{2} {5} \overrightarrow{A B}, \, \, \, \overrightarrow{A F}=\frac{3} {7} \overrightarrow{A D}, \, \, \overrightarrow{A K}=\lambda\overrightarrow{A C}$$,则$${{λ}}$$的值为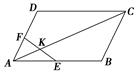
A
A.$$\frac{6} {2 9}$$
B.$$\frac{6} {1 9}$$
C.$$\begin{array} {l l} {\frac{2} {9}} \\ \end{array}$$
D.$$\frac{1} {4}$$
8、['共线向量基本定理', '向量的线性运算']正确率60.0%已知向量$$\overrightarrow{\alpha}, ~ \overrightarrow{\beta},$$且$$\overrightarrow{A B}=\overrightarrow{\alpha}+2 \overrightarrow{\beta}, \; \; \overrightarrow{B C}=-5 \overrightarrow{\alpha}+6 \overrightarrow{\beta}, \; \; \overrightarrow{C D}=7 \overrightarrow{\alpha}-2 \overrightarrow{\beta},$$则一定共线的三点是$${{(}{)}}$$
A
A.$$A, ~ B, ~ D$$
B.$$A, ~ B, ~ C$$
C.$$B, ~ C, ~ D$$
D.$$A, ~ C, ~ D$$
9、['共线向量基本定理', '平面向量基本定理', '利用基本不等式求最值']正确率40.0%在$${{△}{A}{B}{C}}$$中,点$${{D}}$$满足$$\overrightarrow{B D}=2 \overrightarrow{D C}, \; \; E$$为$${{A}{D}}$$上一点,且$$\overrightarrow{B E}=m \overrightarrow{B A}+n \overrightarrow{B C} \left( m > 0, n > 0 \right),$$则$${{m}{n}}$$的最大值为
A
A.$$\frac{1} {6}$$
B.$$\frac{1} {4}$$
C.$$\frac{1} {3}$$
D.$$\frac{1} {2}$$
10、['共线向量基本定理', '平面向量基本定理']正确率60.0%已知$${{D}}$$为$${{△}{A}{B}{C}}$$的边$${{A}{B}}$$上一点,且$$\overrightarrow{C D}=\frac{1} {2} \overrightarrow{A B}+\lambda\overrightarrow{A C},$$则实数$${{λ}}$$的值为()
B
A.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
B.$${{−}{1}}$$
C.$${{1}}$$
D.$$- \frac{4} {3}$$
1. 解析:
① 由 $$| \overrightarrow{a}+\overrightarrow{b} |=| \overrightarrow{a}-\overrightarrow{b} |$$ 平方得 $$|\overrightarrow{a}|^2 + 2\overrightarrow{a} \cdot \overrightarrow{b} + |\overrightarrow{b}|^2 = |\overrightarrow{a}|^2 - 2\overrightarrow{a} \cdot \overrightarrow{b} + |\overrightarrow{b}|^2$$,化简得 $$\overrightarrow{a} \cdot \overrightarrow{b} = 0$$,即 $$\overrightarrow{a}$$ 与 $$\overrightarrow{b}$$ 垂直,不一定共线,命题错误。
② 函数 $$f(x) = \cos(\sin x)$$ 的最小正周期为 $$\pi$$,因为 $$\cos(\sin(x+\pi)) = \cos(-\sin x) = \cos(\sin x)$$,命题正确。
③ 在 $$\triangle ABC$$ 中,由边长可知为直角三角形,$$\angle C = 90^\circ$$。$$\overrightarrow{AB} \cdot \overrightarrow{BC} = |\overrightarrow{AB}| \cdot |\overrightarrow{BC}| \cdot \cos(180^\circ - \angle B) = 5 \times 4 \times (-\frac{4}{5}) = -16$$,命题错误。
④ 函数 $$f(x) = \tan(2x - \frac{\pi}{3})$$ 的对称中心满足 $$2x - \frac{\pi}{3} = \frac{k\pi}{2}$$,解得 $$x = \frac{k\pi}{4} + \frac{\pi}{6}$$。当 $$k=1$$ 时,$$x = \frac{5\pi}{12}$$,命题正确。
综上,正确命题为②④,选 A。
2. 解析:
由 $$\overrightarrow{a} \parallel \overrightarrow{b}$$,得 $$\frac{x}{3} = \frac{3}{1}$$,解得 $$x = 9$$,选 A。
3. 解析:
由 $$2 \overrightarrow{OA} - 7 \overrightarrow{OB} - 3 \overrightarrow{OC} = \overrightarrow{0}$$,整理得 $$\overrightarrow{OA} = \frac{7}{2} \overrightarrow{OB} + \frac{3}{2} \overrightarrow{OC}$$。设 $$\triangle ABC$$ 面积为 $$S$$,$$\triangle BOC$$ 面积为 $$S_1$$,则 $$\frac{S}{S_1} = \frac{|\overrightarrow{OA} \times \overrightarrow{OB} + \overrightarrow{OB} \times \overrightarrow{OC} + \overrightarrow{OC} \times \overrightarrow{OA}|}{|\overrightarrow{OB} \times \overrightarrow{OC}|}$$。代入计算得比值为 $$\frac{12}{7}$$,选 C。
4. 解析:
由 $$\overrightarrow{AG} = \frac{1}{3} \overrightarrow{AB} + \lambda \overrightarrow{AC}$$,且 $$G$$ 在 $$CD$$ 上,设 $$\overrightarrow{CG} = k \overrightarrow{CD}$$。由 $$D$$ 为 $$AB$$ 中点,$$\overrightarrow{CD} = \frac{1}{2} \overrightarrow{AB} - \overrightarrow{AC}$$。代入得 $$\lambda = \frac{1}{3}k$$ 且 $$\frac{1}{3} = \frac{1}{2}k$$,解得 $$\lambda = \frac{1}{6}$$,选 A。
5. 解析:
取 $$BC$$ 中点 $$M$$,则 $$\overrightarrow{AB} + \overrightarrow{AC} = 2 \overrightarrow{AM}$$。$$\overrightarrow{AP} \cdot (\overrightarrow{AB} + \overrightarrow{AC}) = 2 \overrightarrow{AP} \cdot \overrightarrow{AM}$$。由等腰三角形性质,$$AM = \sqrt{9-4} = \sqrt{5}$$,且 $$\overrightarrow{AP} \cdot \overrightarrow{AM} = |\overrightarrow{AM}|^2 = 5$$,故结果为 $$10$$,为定值,选 A。
6. 解析:
由 $$\overrightarrow{AN} = \frac{1}{3} \overrightarrow{AC}$$,设 $$\overrightarrow{BP} = k \overrightarrow{BN}$$。由 $$\overrightarrow{AP} = \overrightarrow{AB} + \overrightarrow{BP} = \overrightarrow{AB} + k (\overrightarrow{AN} - \overrightarrow{AB}) = (1-k) \overrightarrow{AB} + \frac{k}{3} \overrightarrow{AC}$$。与给定条件比较得 $$m = \frac{k}{3}$$ 且 $$\frac{2}{3} = 1-k$$,解得 $$m = \frac{1}{9}$$,选 B。
7. 解析:
设 $$\overrightarrow{AB} = \overrightarrow{a}$$,$$\overrightarrow{AD} = \overrightarrow{b}$$,则 $$\overrightarrow{EF} = \overrightarrow{AF} - \overrightarrow{AE} = \frac{3}{7} \overrightarrow{b} - \frac{2}{5} \overrightarrow{a}$$。由 $$K$$ 在 $$EF$$ 上,设 $$\overrightarrow{AK} = t \overrightarrow{AE} + (1-t) \overrightarrow{AF}$$。又 $$\overrightarrow{AK} = \lambda \overrightarrow{AC} = \lambda (\overrightarrow{a} + \overrightarrow{b})$$,联立解得 $$\lambda = \frac{6}{29}$$,选 A。
8. 解析:
计算 $$\overrightarrow{AD} = \overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CD} = (\overrightarrow{\alpha} + 2\overrightarrow{\beta}) + (-5\overrightarrow{\alpha} + 6\overrightarrow{\beta}) + (7\overrightarrow{\alpha} - 2\overrightarrow{\beta}) = 3\overrightarrow{\alpha} + 6\overrightarrow{\beta} = 3(\overrightarrow{\alpha} + 2\overrightarrow{\beta}) = 3 \overrightarrow{AB}$$,故 $$A, B, D$$ 三点共线,选 A。
9. 解析:
由 $$\overrightarrow{BD} = 2 \overrightarrow{DC}$$,得 $$\overrightarrow{AD} = \frac{1}{3} \overrightarrow{AB} + \frac{2}{3} \overrightarrow{AC}$$。设 $$\overrightarrow{BE} = k \overrightarrow{BA} + (1-k) \overrightarrow{BD}$$,代入得 $$m = k$$,$$n = \frac{2(1-k)}{3}$$。由 $$m, n > 0$$,得 $$0 < k < 1$$。$$mn = k \cdot \frac{2(1-k)}{3} \leq \frac{1}{6}$$,当 $$k = \frac{1}{2}$$ 时取最大值,选 A。
10. 解析:
由 $$\overrightarrow{CD} = \frac{1}{2} \overrightarrow{AB} + \lambda \overrightarrow{AC}$$,且 $$\overrightarrow{CD} = \overrightarrow{AD} - \overrightarrow{AC}$$,设 $$\overrightarrow{AD} = k \overrightarrow{AB}$$,得 $$k \overrightarrow{AB} - \overrightarrow{AC} = \frac{1}{2} \overrightarrow{AB} + \lambda \overrightarrow{AC}$$。比较系数得 $$k = \frac{1}{2}$$,$$\lambda = -1$$,选 B。
.jpg)