.jpg)
正确率60.0%设$${{a}{，}{b}}$$为非零向量 ，$$\lambda， \mu\in{\bf R}，$$则下列命题为真命题的是（）
D
A.若$$\boldsymbol{a} \cdot( \boldsymbol{a}-\boldsymbol{b} )=0，$$则$${{a}{=}{b}}$$
B.若$${{b}{=}{λ}{a}}$$，则$$| \boldsymbol{a} |+| \boldsymbol{b} |=| \boldsymbol{a}+\boldsymbol{b} |$$
C.若$$\lambda\boldsymbol{a}+\mu\boldsymbol{b}=0$$，则$$\lambda=\mu=0$$
D.若$$\mid a \mid> \mid b \mid，$$则$$( a+b ) \cdot( a-b ) > 0$$
正确率40.0%如图所示，半圆的直径$${{A}{B}}$$＝$${{2}}$$，$${{O}}$$为圆心，$${{C}}$$是半圆上不同于$${{A}}$$，$${{B}}$$的任意一点，若$${{P}}$$为半径$${{O}{C}}$$上的动点，则$$( \overrightarrow{P A}+\overrightarrow{P B} ) \cdot\overrightarrow{P C}$$的最小值是（）
C
A.$$\frac{1} {2}$$
B.$$\begin{array} {l l} {\frac{2} {3}} \\ \end{array}$$
C.$$- \frac{1} {2}$$
D.$$\frac{1} {4}$$
3、['平面向量的概念'， '相反向量']正确率60.0%已知点$${{C}}$$在线段$${{A}{B}}$$的延长线上，且$$2 | \overrightarrow{B C} |=| \overrightarrow{A B} |， \; \; \overrightarrow{B C}=\lambda\overrightarrow{C A}.$$等于（）
D
A.$${{3}}$$
B.$$\frac{1} {3}$$
C.$${{−}{3}}$$
D.$$- \frac{1} {3}$$
4、['平面向量的概念'， '相反向量']正确率60.0%给出下列说法：$$( 1 ) \ \overrightarrow{A B} > \overrightarrow{C D} ; \ \ ( 2 )$$方向不同的两个向量一定不平行；$${（{3}{）}}$$两个平行向量的方向相同或相反；$${（{4}{）}}$$若$$\overrightarrow{A B}$$与$$\overrightarrow{C D}$$是共线向量，则$$A， ~ B， ~ C， ~ D$$四点共线，其中正确说法的个数是（）
A
A.$${{0}}$$
B.$${{1}}$$
C.$${{2}}$$
D.$${{3}}$$
5、['平面向量的概念'， '数量积的性质'， '相反向量']正确率60.0%下列命题中，正确的个数是$${{(}{)}}$$
$${①}$$单位向量都相等$${②}$$模相等的两个平行向量是相等向量
$${③}$$若$$\overrightarrow{a} / / \overrightarrow{b}， \overrightarrow{b} / / \overrightarrow{c}，$$则$${{a}^{→}{{/}{/}}{{c}^{→}}}$$$$\textcircled{\oplus} \overrightarrow{a} \left( \overrightarrow{b} \cdot\overrightarrow{c} \right) \mathbb{=} ( \overrightarrow{a} \cdot\overrightarrow{b} ) \overrightarrow{c}$$
$${⑤}$$ 若$${{a}^{→}{=}{{b}^{→}}}$$ 则$$\overrightarrow{a} \cdot\overrightarrow{c}=\overrightarrow{b} \cdot\overrightarrow{c}$$
B
A.$${{0}}$$个
B.$${{1}}$$个
C.$${{2}}$$个
D.$${{3}}$$个
6、['向量加法的定义及运算法则'， '向量减法的定义及运算法则'， '向量的模'， '向量的数量积的定义'， '相反向量']正确率60.0%已知下面四个命题：$$( 1 ) \overrightarrow{A B}+\overrightarrow{B A}=\overrightarrow{0}， \; \; ( 2 ) \overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}， \; \; ( 3 ) \overrightarrow{A B}-\overrightarrow{A C}=\overrightarrow{B C}， \; \; ( 4 ) \overrightarrow{0} \cdot\overrightarrow{A B}=0 ; \; \; ( 5 ) \left| \overrightarrow{a} \right|=\sqrt{a^{-2}}$$.其中正确命题的个数为$${{(}{)}}$$
B
A.$${{2}}$$个
B.$${{3}}$$个
C.$${{4}}$$个
D.$${{5}}$$个
7、['向量加法的定义及运算法则'， '向量减法的定义及运算法则'， '向量数乘的定义与运算律'， '相反向量']正确率60.0%如图，$${{O}}$$在$$\backslash\mathrm{D e l t a \ A B C}$$的内部，$${{D}}$$为$${{A}{B}}$$的中点，且$$\overrightarrow{O A}_{+}$$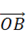
$${{+}}$$
B
A.$${{3}}$$
B.$${{4}}$$
C.$${{5}}$$
D.$${{6}}$$
8、['数量积的性质'， '平面向量的概念'， '充分、必要条件的判定'， '向量的夹角'， '相反向量']正确率60.0%若 $${{a}}$$， $${{b}}$$均为非零向量，则 $${{a}}$$$${{⋅}}$$ $${{b}}$$$${＝{|}}$$ $${{a}}$$$${{|}{|}}$$ $${{b}}$$$${{|}}$$是 $${{a}}$$与 $${{b}}$$共线的（）
A
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分又不必要条件
9、['平面向量加法、减法的坐标运算'， '向量的模'， '向量坐标与向量的数量积'， '向量的夹角'， '相反向量']正确率60.0%已知向量$$\overrightarrow{A B}$$与$$\vec{a}=( 6，-8 )$$的夹角为$${{π}}$$，且$$| \overrightarrow{A B} |=| \overrightarrow{a} |$$，若$${{A}}$$点的坐标为$$(-1， 2 )$$，则$${{B}}$$点的坐标为（）
A
A.$$(-7， 1 0 )$$
B.$$( 7， 1 0 )$$
C.$$( 5，-6 )$$
D.$$(-5， 6 )$$
10、['向量加法的定义及运算法则'， '向量减法的定义及运算法则'， '相反向量']正确率60.0%已知平面内$${{M}}$$，$${{N}}$$，$${{P}}$$三点满足$$\overrightarrow{M N}-\overrightarrow{P N}+\overrightarrow{P M}=\overrightarrow{0}$$，则下列说法正确的是 （）
C
A.$${{M}}$$，$${{N}}$$，$${{P}}$$是一个三角形的三个顶点
B.$${{M}}$$，$${{N}}$$，$${{P}}$$是一条直线上的三个点
C.$${{M}}$$，$${{N}}$$，$${{P}}$$是平面内的任意三个点
D.以上都不对
1. 解析：
选项分析：
A. 由 $$a \cdot (a - b) = 0$$ 得 $$|a|^2 - a \cdot b = 0$$，即 $$a \cdot b = |a|^2$$，但这并不意味着 $$a = b$$，反例：$$a$$ 和 $$b$$ 夹角为 0 且 $$|b| = |a|$$ 时成立，但 $$a$$ 和 $$b$$ 可以不同。
B. 若 $$b = \lambda a$$，则 $$|a| + |b| = |a| + |\lambda a| = (1 + |\lambda|)|a|$$，而 $$|a + b| = |(1 + \lambda)a| = |1 + \lambda||a|$$。当 $$\lambda > 0$$ 时，$$1 + |\lambda| = 1 + \lambda$$，等式成立；但当 $$\lambda < 0$$ 时，等式不成立。
C. 若 $$\lambda a + \mu b = 0$$，且 $$a$$ 和 $$b$$ 不共线，则 $$\lambda = \mu = 0$$；但如果 $$a$$ 和 $$b$$ 共线，$$\lambda$$ 和 $$\mu$$ 可以不全为 0。
D. 由 $$|a| > |b|$$，则 $$(a + b) \cdot (a - b) = |a|^2 - |b|^2 > 0$$，命题成立。
综上，正确答案为 D。
2. 解析：
设半圆圆心 $$O$$ 为坐标原点，$$AB$$ 为 $$x$$ 轴，$$A(-1, 0)$$，$$B(1, 0)$$，$$C(\cos \theta, \sin \theta)$$，$$P$$ 在 $$OC$$ 上，设 $$P(t \cos \theta, t \sin \theta)$$，$$t \in [0, 1]$$。
计算向量：
$$\overrightarrow{PA} = (-1 - t \cos \theta, -t \sin \theta)$$
$$\overrightarrow{PB} = (1 - t \cos \theta, -t \sin \theta)$$
$$\overrightarrow{PC} = (\cos \theta - t \cos \theta, \sin \theta - t \sin \theta) = (1 - t)(\cos \theta, \sin \theta)$$
则 $$(\overrightarrow{PA} + \overrightarrow{PB}) \cdot \overrightarrow{PC} = (-2t \cos \theta, -2t \sin \theta) \cdot ((1 - t)\cos \theta, (1 - t)\sin \theta)$$
$$= -2t(1 - t)(\cos^2 \theta + \sin^2 \theta) = -2t(1 - t)$$
求最小值：$$-2t(1 - t)$$ 在 $$t \in [0, 1]$$ 的最小值为 $$- \frac{1}{2}$$（当 $$t = \frac{1}{2}$$ 时）。
正确答案为 C。
3. 解析：
设 $$A$$、$$B$$、$$C$$ 在数轴上，$$A = 0$$，$$B = 1$$，则 $$C = 1 + 2 = 3$$（因为 $$2|BC| = |AB|$$，即 $$2 \times 2 = 2$$，这里需要重新设定）。
更准确设定：设 $$AB = 1$$，$$BC = \frac{1}{2}$$，则 $$C = B + BC = 1 + \frac{1}{2} = \frac{3}{2}$$。
$$\overrightarrow{CA} = A - C = -\frac{3}{2}$$，$$\overrightarrow{BC} = \frac{1}{2}$$。
由 $$\overrightarrow{BC} = \lambda \overrightarrow{CA}$$，得 $$\frac{1}{2} = \lambda \left(-\frac{3}{2}\right)$$，解得 $$\lambda = -\frac{1}{3}$$。
正确答案为 D。
4. 解析：
说法分析：
(1) 向量不能比较大小，错误。
(2) 方向不同的向量可能平行（方向相反），错误。
(3) 平行向量的方向相同或相反，正确。
(4) $$\overrightarrow{AB}$$ 与 $$\overrightarrow{CD}$$ 共线，不保证 $$A, B, C, D$$ 四点共线（可能平行），错误。
综上，只有 (3) 正确，正确答案为 B。
5. 解析：
命题分析：
① 单位向量方向不一定相同，错误。
② 模相等的平行向量方向可以相反，不一定是相等向量，错误。
③ 若 $$b = 0$$，则 $$a$$ 和 $$c$$ 不一定平行，错误。
④ $$a(b \cdot c)$$ 是向量，$$(a \cdot b)c$$ 也是向量，但一般情况下不相等，错误。
⑤ 若 $$a = b$$，则 $$a \cdot c = b \cdot c$$ 成立，正确。
综上，只有 ⑤ 正确，正确答案为 B。
6. 解析：
命题分析：
(1) $$\overrightarrow{AB} + \overrightarrow{BA} = \overrightarrow{AB} - \overrightarrow{AB} = 0$$，正确。
(2) 向量加法定义，正确。
(3) $$\overrightarrow{AB} - \overrightarrow{AC} = \overrightarrow{CB} \neq \overrightarrow{BC}$$，错误。
(4) 零向量与任何向量的点积为 0，正确。
(5) $$|\overrightarrow{a}| = \sqrt{a^2}$$ 写法不规范，但含义正确（假设 $$a^{-2}$$ 为 $$a^2$$ 的笔误）。
综上，正确的有 (1)、(2)、(4)、(5)，共 4 个，正确答案为 C。
7. 解析：
题目描述不完整，无法解析。
8. 解析：
$$a \cdot b = |a||b|$$ 等价于 $$a$$ 和 $$b$$ 同向（夹角为 0），是共线的充分条件；但共线时 $$a \cdot b = \pm |a||b|$$，不一定是同向。因此是充分不必要条件。
正确答案为 A。
9. 解析：
$$\overrightarrow{a} = (6, -8)$$，$$|\overrightarrow{a}| = 10$$，$$\overrightarrow{AB}$$ 与 $$\overrightarrow{a}$$ 夹角为 $$\pi$$，说明 $$\overrightarrow{AB} = -\overrightarrow{a} = (-6, 8)$$。
设 $$B(x, y)$$，则 $$\overrightarrow{AB} = (x + 1, y - 2) = (-6, 8)$$，解得 $$x = -7$$，$$y = 10$$。
正确答案为 A。
10. 解析：
由 $$\overrightarrow{MN} - \overrightarrow{PN} + \overrightarrow{PM} = 0$$，化简得 $$\overrightarrow{MN} + \overrightarrow{NP} + \overrightarrow{PM} = 0$$，即 $$\overrightarrow{MP} + \overrightarrow{PM} = 0$$，恒成立。
因此，$$M, N, P$$ 可以是平面内任意三个点，正确答案为 C。