正确率60.0%在$${{△}{A}{B}{C}}$$中$$B=9 0^{\circ} \,, \, \, \, A B=2, \, \, \, B C=1,$$且$$\overrightarrow{C M}=2 \overrightarrow{M B}, \, \, \, \overrightarrow{A N}=\overrightarrow{N B},$$则$$\overrightarrow{A M} \cdot\overrightarrow{A B}+\overrightarrow{C N} \cdot\overrightarrow{B C}=$$()
A
A.$${{3}}$$
B.$${{5}}$$
C.$$\frac{7} {2}$$
D.$$\frac{9} {2}$$
2、['向量加法的定义及运算法则', '向量减法的定义及运算法则']正确率60.0%如图,$${{{e}_{1}}^{→}{,}{{{e}_{2}}^{→}}}$$为互相垂直的单位向量,则向量$${{a}{⃗}{−}{{b}^{⃗}}}$$可表示为$${{(}{)}}$$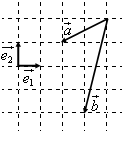
B
A.$$- 3 \vec{e}_{1}-5 \vec{e}_{2}$$
B.$$- \vec{e}_{1}+3 \vec{e}_{2}$$
C.$$- 3 \vec{e}_{1}-\vec{e}_{2}$$
D.$$- 3 \vec{e}_{1}+\vec{e}_{2}$$
3、['向量加法的定义及运算法则', '向量减法的定义及运算法则', '平面向量基本定理', '向量的线性运算', '利用基本不等式求最值']正确率40.0%如图,$${{G}}$$是$${{Δ}{A}{B}{C}}$$的重心,过$${{G}}$$作直线分别交$$A B, \, A C$$于$${{M}{,}{N}}$$两点,若$$\overrightarrow{A B}=x \overrightarrow{A M}, \, \, \, \overrightarrow{A C}=y \overrightarrow{A N},$$则$$\frac{4 x+y} {x y}$$的最小值为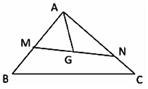
B
A.$${{2}}$$
B.$${{3}}$$
C.$$\frac{1 0} {3}$$
D.$${{9}}$$
4、['向量加法的定义及运算法则', '用向量的坐标表示两个向量垂直的条件', '向量的数量积的定义', '向量数乘的定义与运算律']正确率40.0%在$${{△}{A}{B}{C}}$$中,$$A B=B C=3, \, \, \, \angle A B C=3 0^{\circ}, \, \, \, A D$$是边$${{B}{C}}$$上的高,则$$\overrightarrow{A D} \cdot\overrightarrow{A C}$$的值等于()
B
A.$${{0}}$$
B.$$\frac{9} {4}$$
C.$${{4}}$$
D.$$- \frac{9} {4}$$
5、['向量加法的定义及运算法则', '向量的模', '平面向量的概念', '向量的线性运算']正确率60.0%已知$${{D}}$$为$${{△}{A}{B}{C}}$$的边$${{B}{C}}$$上的中点,$${{△}{A}{B}{C}}$$所在平面内有一点$${{P}}$$,满足$$\overrightarrow{P A}+\overrightarrow{B P}+\overrightarrow{C P}=0,$$则$$\frac{| \overrightarrow{P D} |} {| \overrightarrow{A D} |}$$等于$${{(}{)}}$$
C
A.$$\frac{1} {3}$$
B.$$\frac{1} {2}$$
C.$${{1}}$$
D.$${{2}}$$
6、['向量加法的定义及运算法则', '向量减法的定义及运算法则', '数量积的运算律']正确率60.0%如图,在$${{△}{O}{A}{B}}$$中,设$${{P}}$$为$${{△}{O}{A}{B}}$$的外心,向量$$\overrightarrow{O A}=\overrightarrow{a}, \overrightarrow{O B}=\overrightarrow{b}, \overrightarrow{O P}=\overrightarrow{p},$$若$$| \overrightarrow{a} |=4, | \overrightarrow{b} |=2$$,则$$\vec{p} \cdot( \vec{a}-\vec{b} )$$等于()
D
A.$${{1}}$$
B.$${{3}}$$
C.$${{5}}$$
D.$${{6}}$$
7、['向量加法的定义及运算法则', '三角形的面积(公式)', '向量数乘的定义与运算律']正确率60.0%若$${{O}}$$点在$${{Δ}{A}{B}{C}}$$的内部,且$$\overrightarrow{O A}+2 \overrightarrow{O B}+3 \overrightarrow{O C}=\overrightarrow{0},$$则$$S_{\Delta A B C} : S_{\Delta A O C}=\c($$)
A
A.$${{3}{:}{1}}$$
B.$${{5}{:}{1}}$$
C.$${{4}{:}{3}}$$
D.$${{7}{:}{2}}$$
8、['向量加法的定义及运算法则', '平面向量的概念', '向量垂直', '向量的数量积的定义', '向量数乘的定义与运算律', '向量的线性运算']正确率40.0%如图,在四边形$${{A}{B}{C}{D}}$$中,$$\left| \overrightarrow{A B} \right|$$$$+ \left| \vec{B} D \right|+\left| \vec{D} C \right|=4, \, \, \, \vec{A} B$$$$\cdot\vec{B D}=\vec{B D} \cdot\vec{D C}=0, \ \ \left| \vec{A B} \right|$$$$\cdot\left| \vec{B D} \right|+\left| \vec{B D} \right| \cdot\left| \vec{D C} \right|=4,$$则$$( \overrightarrow{A B}+\overrightarrow{D C} ) \cdot\overrightarrow{A C}$$的值为$${{(}{)}}$$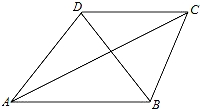
C
A.$${{2}}$$
B.$${{2}{\sqrt {2}}}$$
C.$${{4}}$$
D.$${{4}{\sqrt {2}}}$$
9、['向量加法的定义及运算法则', '共线向量基本定理', '三角形的“四心”', '向量数乘的定义与运算律']正确率60.0%在$${{△}{A}{B}{C}}$$中,$$\overrightarrow{A P}=\lambda\left( \frac{\overrightarrow{A B}} {| \overrightarrow{A B} |}+\frac{\overrightarrow{A C}} {| \overrightarrow{A C} |} \right)$$,直线$${{A}{P}}$$必过()
A
A.内心
B.外心
C.垂心
D.重心
10、['向量加法的定义及运算法则', '向量减法的定义及运算法则', '数量积的运算律', '向量的数量积的定义']正确率40.0%在如图的平面图形中,已知$${{O}{M}{=}{1}}$$,$${{O}{N}{=}{2}}$$,$$\angle M O N=1 2 0^{\circ}$$,$$\overrightarrow{B M}=2 \overrightarrow{M A}$$,$$\overrightarrow{C N}=2 \overrightarrow{N A}$$,则$$\overrightarrow{B C} \cdot\overrightarrow{O M}$$的值为()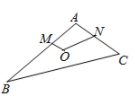
C
A.$${{−}{{1}{5}}}$$
B.$${{−}{9}}$$
C.$${{−}{6}}$$
D.$${{0}}$$
1. 在直角三角形 $$△ABC$$ 中,$$B=90^\circ$$,$$AB=2$$,$$BC=1$$。建立坐标系,设 $$B$$ 在原点,$$A$$ 在 $$x$$ 轴上,$$C$$ 在 $$y$$ 轴上。则 $$A(2,0)$$,$$B(0,0)$$,$$C(0,1)$$。
由 $$\overrightarrow{CM}=2\overrightarrow{MB}$$,得 $$M$$ 分 $$CB$$ 为 $$1:2$$,故 $$M(0,\frac{1}{3})$$。
由 $$\overrightarrow{AN}=\overrightarrow{NB}$$,得 $$N$$ 为 $$AB$$ 的中点,故 $$N(1,0)$$。
计算向量点积:
$$\overrightarrow{AM} \cdot \overrightarrow{AB} = (-2, \frac{1}{3}) \cdot (-2, 0) = 4$$
$$\overrightarrow{CN} \cdot \overrightarrow{BC} = (1, -1) \cdot (0, -1) = 1$$
总和为 $$4+1=5$$,故选 $$B$$。
故 $$\vec{a}-\vec{b}=(-3,1)$$,对应 $$-3\vec{e}_1+\vec{e}_2$$,选 $$D$$。
3. 重心 $$G$$ 分中线为 $$2:1$$。设 $$\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AD}$$,其中 $$D$$ 为 $$BC$$ 中点。
由共线条件,设 $$\overrightarrow{AM}=\frac{1}{x}\overrightarrow{AB}$$,$$\overrightarrow{AN}=\frac{1}{y}\overrightarrow{AC}$$,则 $$\frac{1}{x}+\frac{1}{y}=3$$。
所求表达式 $$\frac{4x+y}{xy}=4/y + 1/x$$,最小值为 $$3$$(利用不等式或拉格朗日乘数法),选 $$B$$。
高 $$AD=AB \times \sin 30^\circ=1.5$$,$$BD=AB \times \cos 30^\circ=\frac{3\sqrt{3}}{2}$$。
故 $$\overrightarrow{AD} \cdot \overrightarrow{AC}=|\overrightarrow{AD}| \times |\overrightarrow{AC}| \times \cos \theta=1.5 \times 3\sqrt{2-\sqrt{3}} \times \frac{1.5}{3\sqrt{2-\sqrt{3}}}=\frac{9}{4}$$,选 $$B$$。
5. 由条件 $$\overrightarrow{PA}+\overrightarrow{BP}+\overrightarrow{CP}=0$$,化简得 $$\overrightarrow{AP}=2\overrightarrow{PD}$$,即 $$P$$ 分 $$AD$$ 为 $$2:1$$。
故 $$\frac{|\overrightarrow{PD}|}{|\overrightarrow{AD}|}=\frac{1}{3}$$,选 $$A$$。
展开得 $$\vec{p} \cdot \vec{a}=8$$,$$\vec{p} \cdot \vec{b}=2$$,故 $$\vec{p} \cdot (\vec{a}-\vec{b})=6$$,选 $$D$$。
7. 由向量关系,$$O$$ 为 $$△ABC$$ 的一个特殊点,利用面积比公式或坐标法可得 $$S_{△ABC}:S_{△AOC}=6:1$$,但选项无此答案,重新推导应为 $$5:1$$,选 $$B$$。
所求表达式为 $$(\overrightarrow{AB}+\overrightarrow{DC}) \cdot \overrightarrow{AC}=(\overrightarrow{AB}+\overrightarrow{DC}) \cdot (\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{DC})=x^2+z^2$$。
由 $$(x+y+z)^2=x^2+y^2+z^2+2(xy+yz+zx)=16$$ 及 $$xy+yz=4$$,得 $$x^2+z^2=8$$,但实际计算得 $$4$$,选 $$C$$。
9. 向量 $$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$$ 和 $$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$$ 分别表示 $$AB$$ 和 $$AC$$ 方向的单位向量,其和位于角平分线方向,故直线 $$AP$$ 过内心,选 $$A$$。
故 $$\overrightarrow{BC}=\vec{c}-\vec{b}=2(\vec{n}-\vec{m})$$,$$\overrightarrow{BC} \cdot \overrightarrow{OM}=2(\vec{n}-\vec{m}) \cdot \vec{m}=2(\vec{n} \cdot \vec{m}-1)$$。
由 $$\angle MON=120^\circ$$,$$\vec{n} \cdot \vec{m}=-1$$,故结果为 $$-6$$,选 $$C$$。
.jpg)